Lösungen der Aufgaben zum Konzept der Energie
(Kursstufe > Das Konzept der Energie)
Inhaltsverzeichnis
Energiebedarf eines Menschen
Ein Mensch benötigt täglich etwa 10000 kJ Energie, die er durch das Essen erhält. (genauere Werte findet man zB. bei Wikipedia.)
- Berechnen Sie die mittlere Leistung in Watt.
Die Leistung ist [math]\frac{Energie}{Zeit} = \frac{10000\,\rm kJ}{1\,\rm d}= \frac{10000\,\rm kJ}{24\cdot 60\cdot 60\,\rm s} = 0{,}115\,\rm kW = 116\,\rm W[/math]
100g Nudeln haben einen Brennwert von 1400 kJ.
- b) Berechne das chemische Potential der Nudeln in kJ/kg.
Das Potential beträgt [math]14000 \,\rm\tfrac{kJ}{kg}[/math].
- c) Berechne welche Menge an Nudeln man pro Tag und wieviel pro Stunde essen müsste, wenn man seinen Energiebedarf ausschließlich mit Nudeln deckt.
Zwischen Energiemenge und Träger gilt hier, wegen des konstanten Potentials: [math]Energie = Brennwert \cdot Tr\ddot agermenge[/math]
Also folgt für die Trägermenge (Nudelmenge) pro Tag:
- [math]Nudelmenge=\frac{10000\,\rm kJ}{140\,\rm kJ/kg} = 0{,}714\,\rm kg=714\,\rm g[/math]
Und pro Stunde dementsprechend nur [math]30\,\rm g[/math].
Man kann das auch mit der Leistung eines Menschen ausrechnen:
- [math]P=I_T \cdot \varphi \quad \Rightarrow \quad I_T = \frac{P}{\varphi}[/math]
- [math]\frac{Nudeln}{Zeit}= I_T=\frac{116\,\rm W}{14000\,\rm kJ/kg} = 8{,}3 \cdot 10^{-5}\frac{\rm kg}{\rm s}=8{,}3 \frac{\rm mg}{\rm s} = 30 \frac{\rm g}{\rm h}= 0{,}714 \frac{\rm kg}{\rm d}[/math]
Ein Mühlrad
Auf ein Mühlrad fließen pro Stunde 18000 Liter Wasser. Das Mühlrad hat einen Durchmesser von 3m.
- a) Welche Leistung hat die Mühle maximal? (Gesucht ist also die Energiemenge pro Sekunde.)
Für die Leistung gilt: [math]P = gh \, \frac{Wassermasse}{Zeit} = 30 \frac{\rm J}{\rm kg}\cdot \frac{18000\,\rm kg}{3600\,\rm s} = 150\,\rm W[/math]
- b) Beschreiben Sie die Energieaufnahme des Mühlrads mit einem Trägerstrom und dem zugehörigen Potential. Vergleichen Sie dies mit der Nahrungsaufnahme eines Menschen.
Bei der Nahrungsaufnahme tragen die Nudeln die Energie, beim Wasserrad das Wasser. So wie das Wasser an Höhe verliert, verlieren die Nudeln an chemischen Potential im Darm. Die Endprodukte "niedriges Wasser" und "Kot" sind weniger wertvoll.
Der Energieumsatz hängt beides mal von der Trägermenge pro Zeit und dem Potentialunterschied ab. So hat das Mühlrad bei großem Wasserstrom und großer Höhendifferenz eine große Leistung. Der Mensch, wenn er viel Schokolade ist :). (Wenn man sich dann auch mehr bewegt (!) oder mehr nachdenkt (?) (vgl. Wikipedia: Leistung des Gehirns oder Arbeitsblätter News: Energieverbrauch des Gehirns, Werner Stangl), dann wird die Energie nicht im Fettgewebe gespeichert.)
Ein Staubsauger
Auf einem Staubsauger steht:
Maximale Leistung: 1500W
- Wie groß ist die elektrische Stromstärke? (Gesucht ist also die Ladungsmenge, die in einer Sekunde durch den Sauger fließt.)
Mit [math]P = U \, I[/math] folgt:
- [math]I=\frac{P}{U}=\frac{1500\,\rm W}{230\,\rm V} = \frac{1500\,\rm J/s}{230\,\rm J/C} = 6{,}5 \frac{\rm C}{\rm s} = 6{,}5\,\rm A[/math]
- Vergleichen Sie den Staubsauger mit dem Mühlrad.
Hier trägt die elektrische Ladung die Energie. Der Energieumsatz ist groß, wenn viel Ladung fließt und diese viel Energie trägt. Die Stromstärke gibt den Ladungsdurchsatz an und die Spannung den Unterschied des Beladungsmaßes (Potentials).
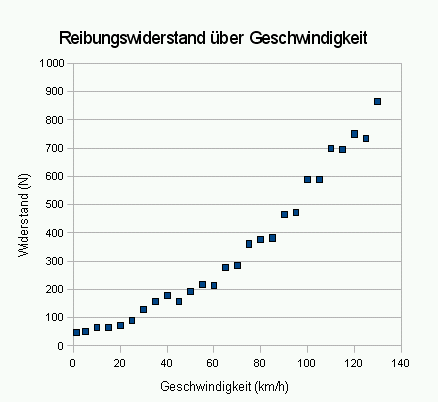
Auto fahren
- Welche Leistung benötigt man, um konstant 50km/h oder konstant 100km/h zu fahren?
Der Widerstand beträgt bei 500 km/h [math]200\,\rm N[/math] und bei 100 km/h [math]550\,\rm N[/math].
Für den Energieumsatz, also die Leistung, gilt:
- [math]P_{50} = v \, F = 8{,}89\,\rm m/s\cdot 200\,\rm N = 2780\,\rm W[/math]
- [math]P_{100} = v \, F = 27{,}78\,\rm m/s\cdot 550\,\rm N = 15280\,\rm W[/math]
Der Energiebedarf pro Zeit steigt also fast auf das 6-fache!
Bemerkenswert ist der geringe Energiebedarf bei 50 km/h. Der Motor hat eine maximale Leistung von ca. 55000 Watt, er ist also bei weitem nicht ausgelastet. Bei diesen geringen Geschwindigkeiten hat er deswegen auch einen schlechten Wirkungsgrad, denn hier geht viel Energie durch die Erwärmung des Motors und der Abgase verloren.
Bei einem Ottomotor (Benziner) explodiert das Luft-Benzin-Gemisch bei einer Temperatur von 2000°C. Die Abgase haben eine Temperatur von lediglich 800°C.
- Warum kann deswegen der Wirkungsgrad dieses Motors nicht über 47% liegen?
Die Entropie ist der Träger der Wärmeenergie. Sie wird bei 2000°C = 2273K bei der Verbrennung erzeugt. Im Motor gibt die Entropie einen Teil ihrer Energie ab, was man am Temperaturabfall auf 1073K sehen kann. Die Energie, die noch in den heißen Abgasen steckt, geht "verloren".
Pro Carnot Entropiemenge steckt man also 2273 Joule hinein und 1073 Joule gehen "verloren". Das entspricht einem Wirkungsgrad von [math]\frac{1073\,\rm J}{2273\,\rm J} = 0{,}47[/math]
- Reale Ottomotoren haben einen Wirkungsgrad von ca. 25%. Welche Eingangsleistung braucht daher der Motor, um 50km/h oder 100km/h zu fahren? (Wieviel Benzin ist dazu nötig? Man kann den Energiegehalt eines Liters mit ca. 32MJ annehmen.
Bei einem Wirkungsgrad von nur 25% wären das
- bei 50 km/h: [math]\frac{2780\,\rm W}{0{,}25}=11120\,\rm W[/math]
- bei 100 km/h: [math]\frac{15280\,\rm W}{0{,}25}=61120\,\rm W[/math]
Für die Benzinmenge gilt:
- [math]P = Brennwert \cdot \frac{Benzinmenge}{Zeit}[/math]
- [math]\frac{Benzinmenge}{Zeit} = \frac{11120\,\rm W}{32000000\,\rm J/l}=3{,}475 \cdot 10^{-4} \frac{\rm l}{\rm s}=1{,}25 \frac{\rm l}{\rm h}[/math]
- [math]\frac{Benzinmenge}{Zeit} = \frac{61120\,\rm W}{32000000\,\rm J/l}=1{,}91 \cdot 10^{-3} \frac{\rm l}{\rm s}=6{,}9 \frac{\rm l}{\rm h}[/math]
Der Benzinbedarf wäre bei der geringen Geschwindigkeit sehr niedrig. Ein realistischer Verbrauch liegt wesentlich höher und zeigt den schlechten Wirkungsgrad des Ottomotors bei geringer Auslastung.
Energiebedarf einer Wärmepumpe
- Vergleiche die Wärmepumpe mit dem Mühlrad. Es gibt einen wesentlichen Unterschied!
Die Wärmepumpe entspricht einem rückwärtslaufendem Mühlrad, also einer Wasserpumpe.
- Wie kann man erklären, dass die Wärmepumpe Energie benötigt?
Die Wärmepumpe bringt die Entropie auf ein höheres Temperaturniveau und braucht dazu Energie, die dann in der Entropie steckt, so wie auch eine Wasserpumpe Energie benötigt, um Wasser nach oben zu pumpen.
- Wie hoch ist der Energiebedarf der Wärmepumpe?
Für die Leistung gilt:
- [math]P = Temperaturunterschied \, \frac{Entropie}{Zeit} = 4\,\rm K \cdot 503\,\rm Ct/s=2012\,\rm W[/math]
Lageenergie eines Wasserturms
- Wieviel Lageenergie steckt wohl in dem Wasser des Turms? Genauer: Wieviel Energie könnte man erhalten, wenn man das Wasser am Fuße des Turmes herauslaufen läßt?
Der Wasserturm ist in etwa 20m breit und die maximale Wasserhöhe beträgt etwa 10m. Die tragende Betonsäule ist ca. 45m lang.
Erste Abschäzung
- Schätzen Sie die mittlere Höhe des Wassers und berechnen so einen ersten Näherungswert.
Die mittlere Höhe beträgt ca. 45m + 7m = 52m. Der Betonkegel hat ein Volumen von [math]\frac{1}{3}\pi\, (10\,\rm m)^2 \cdot 10\,\rm m = 1050\,\rm m^3[/math] In den Wasserturm passen also 1050 t oder 1050000 kg Wasser.
Für die Energie folgt damit: [math]E = gh \, m = 546\,\rm MJ[/math]
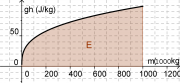
- Bestimmen Sie die Energiemenge durch eine ungefähre Flächenbestimmung. Jedes Rechteck entspricht [math]100000\,\rm kg \cdot 10\frac{\rm J}{\rm kg}=1\,\rm MJ[/math].
Ich habe 75 Rechtecke gezählt. Daraus ergibt sich:
- [math]E = 75 \cdot 1\,\rm MJ = 75\,\rm MJ[/math]
Bei dieser Berechnung ist die Höhe ab Beginn des Betonkegels gerechnet. Es kommt noch die zusätzliche Lageenergie für die 45m Höhe über dem Boden dazu:
- [math]E = g \, 45\,\rm m \, 1050000\,\rm kg + 75\,\rm MJ = 472{,}5 MJ + 75\,\rm MJ = 547{,}5\,\rm MJ[/math]
Es ist etwas mehr als zunächst geschatzt, der Schwerpunkt liegt also etwas höher als geschätzt. (Er liegt 1/4 der Höhe unter der Grundfläche.)