Zusammenfassung: Das elektrische Feld

(Kursstufe > Grundlagen der Feldtheorie und Das elektrische Feld)

Feldlinien und Feldflächen des Zentralfeldes einer positiv geladenen Kugel.

Darstellung eines Dipol-Feldes.

Die Felddarstellung zweier negativer Ladungen.

Der positive Probekörper wird von der positiven Ladung zur negativen gezogen. Man kennzeichnet die Feldlinien mit Pfeilen.

Das Potentialgebirge eines Plattenkondensators. Von der positiven Platte zur negativen Platte geht es "bergab".

Bei weniger Ladung ist die Quellenstärke des Flusses kleiner.

Die "Feldlinendichte" ist ein Maß für die Feldstärke.

Feldtheorie

• Das elektrische Feld vermittelt eine Wechselwirkung zwischen Gegenständen, die elektrische Ladung tragen.

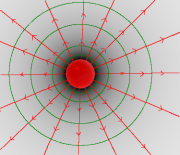
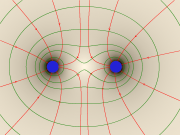
Das elektrische Feld drückt alle Gegenstände mit gleichnamigen elektrischen Ladungen [math]Q[/math] voneinander weg (+ + oder - -)

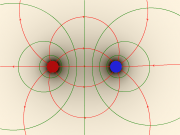
und zieht alle Gegenstände mit ungleichnamigen elektrischen Ladungen aufeinander zu (+ -).

Feldenergie

• Trennt man Ladungen, so speichert das elektrische Feld die dazu nötige Energie.

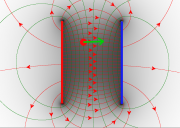
Graphische Darstellung

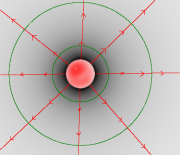
• Die Feldlinien geben die Kraftrichtung auf einen positiven Probekörper an.
• Die Feldflächen stehen senkrecht auf den Linien.

Zug- und Druckspannungen

• Das elektrische Feld steht parallel zu den Linien unter Zugspannung und parallel zu den Flächen unter Druckspannung.

"Feldlinien sind sich abstoßende Gummibänder"

Feldstärke

• Die Feldstärke ist der Ortsfaktor des Feldes an einer Stelle und eine vektorielle Größe.

Sie gibt die auf eine Ladungseinheit normierte Kraftwirkung an:

[math]\vec E=\frac{\vec F}{Q} \quad \Leftrightarrow \quad \vec F=Q\, \vec E[/math]

Potential

• Bewegt man einen Probekörper in einem elektrischen Feld, so speichert das Feld die benötigte Energie oder gibt sie wieder ab.

Diese Energie heißt potentielle Energie.

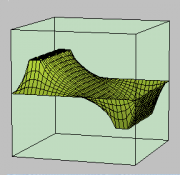
• Der Probekörper bewegt sich im Feld ähnlich wie eine rollende Kugel im Potentialgebirge.

Feldflächen sind Äquipotentialflächen und entsprechen den Höhenlinien im Potentialgebirge.

• Das Potential eines Feldes gibt die auf eine Ladungseinheit normierte potentielle Energie in Bezug auf ein Nullniveau an.

Der Potentialunterschied zwischen zwei Punkten heißt Spannung:

[math]\varphi = \frac{W}{Q}[/math] [math]\textrm{ }\qquad \Delta \varphi = U[/math]

Bewegt sich ein Probekörper mit der Ladung Q die Spannung U herauf (herab), so nimmt die Energie zu (ab) um:

[math]W = Q\,U[/math]

• Die Feldstärke ist die räumliche Änderungsrate des Potentials.

("Steilheit des Potentialgebirges" oder "Feldflächendichte")

[math]E = \varphi' \approx \frac{\Delta \varphi}{\Delta s} = \frac{U}{d}[/math]

Ladung als Quellenstärke

• Die Feldstärke kann man als "Feldliniendichte" interpretieren.

Die "Anzahl der Feldinien" durch eine Fläche als Feldfluss.

• Der Feldfluss durch eine geschlossene Fläche ist gerade die enthaltene Ladung.

Die Feldstärke ist proportional zur Flächenladungsdichte.

Bei einer Feldstärke von 1 N/C und einer Oberfläche von 1m² beträgt die von der Fläche umschloßene Ladung [math]8{,}85 \cdot 10^{-12} \mathrm C[/math].

[math]\epsilon_0 \, E \, A = Q \quad \Leftrightarrow \quad E = \frac{1}{\epsilon_0}\frac{Q}{A} [/math] [math]\text{ }\qquad \varepsilon_0 = 8{,}854 \cdot 10^{-12} \frac {\mathrm{A}\,\mathrm{s}} {\mathrm{V}\,\mathrm{m}}[/math] ist die elektrische Feldkonstante.

Der Kondensator

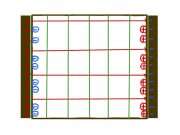
• Ein einfacher Plattenkondensator besteht aus zwei parallelen Platten.

Vereinfachend nimmt man an, dass sich nur zwischen den Platten ein homogenes Feld befindet.

• Einen geladenen Kondensator kann man mit einem aufgepumpten Fahrradreifen vergleichen:

Fahrradreifen	Kondensator
speichert Luft	speichert el. Ladung
Druckenergie der Luft	el. Energie des Feldes
Luftdruck	el. Potential
Druckunterschied	Spannung

Dieser Kondensator hat eine Kapazität von 0,5F. Bei 6V speichert er 3C Ladung und 9J Energie.

Mit Dielektrikum ([math]\epsilon_r=3[/math]) hat der Kondensator eine Kapazität von 1,5F. Bei 6V speichert er 9C Ladung und 27J Energie. Bei 3C Ladung speichert er nur 3J Energie.

• Der konstante Quotient aus Ladung und Spannung eines idealen Kondensators heißt "Kapazität".

Die Kapazität ist proportional zur Plattenfläche und antiproportional zum Plattenabstand.

[math]C=\frac{Q}{U} \quad \Leftrightarrow \quad Q = C\, U \qquad \Leftrightarrow \quad U = \frac{1}{C}\, Q \qquad \rm{mit} \it \qquad C = \epsilon_0 \, \frac{A}{d} \quad \left[ C \, \right]= \rm 1\, Farad \;(F)[/math]

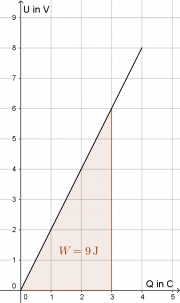
• Die gespeicherte Energie entspricht der Fläche unter der U(Q)-Kennlinie:

[math]E_{el}=\frac{1}{2} \, Q \, U = \frac{1}{2}\, \frac{1}{C}\, Q^2 = \frac{1}{2}\, C \, U^2 [/math]

Die Permittivität dieses Dielektrikums ist [math]\epsilon_r = 3[/math].

• Ein Kondensator mit Dielektrikum der Permittivität [math]\epsilon_r[/math] hat eine um den Faktor [math]\epsilon_r[/math] größere Kapazität:

[math] C = \epsilon_0 \, \epsilon_r \, \frac{A}{d}[/math]

• Bei gleicher Spannung speichert ein Kondensator durch das Dielektrikum [math]\epsilon_r[/math] mal soviel Energie, weshalb auch die Energiedichte steigt:

[math]\rho = \frac{W}{V} = \epsilon_0 \, \epsilon_r \, E^2[/math]

Der Anteil von [math]1/\epsilon_r[/math] wird im elektrischen Feld gespeichert, der Rest im polarisierten Dielektrikum.

• Die Kraft auf die Platten eines idealen Kondensators ohne Dielektrikum beträgt:

[math]F=\frac{1}{2} \, Q \, E = \frac{1}{2}\, \epsilon_0 \,A\,E^2 = \frac{Q^2}{2\epsilon_0\,A} = \frac{W}{d}[/math]