Beschreibung einer harmonischen Schwingung mit einer Differentialgleichung: Unterschied zwischen den Versionen

Version vom 22. Dezember 2010, 23:46 Uhr

Ziel dieser Untersuchung einer Schwingung ist es, von den Eigenschaften des schwingenden Systems auf die Bewegung zu schließen. Damit kann man von z.B. der Masse, der Härte der Feder oder der Stärke der Gravitation, etc. auf Eigenschaften der Schwingung, wie die Frequenz, die maximale Geschwindigkeit, etc schließen.

Man erreicht dies, indem man die wirkende Kraft genauer analysiert.

Als Ergebnis erhält man eine Differentialgleichung, die alle Eigenschaften des schwingenden Systems enthält.

Die Lösung dieser DGL führt zu möglichen Bewegungen dieses Systems. Nicht für alle DGL sind Lösungen leicht zu finden, deshalb betrachtet man den Spezialfall einer harmonischen Schwingung.

Differentialgleichung einer harmonischen Schwingung

Die Ausgangssituation.

Zusammenhang von Ort und Rückstellkraft.

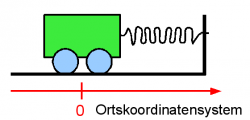
• Man betrachtet eine vereinfachte Situation: Ein Körper wird als punktförmige Masse idealisiert, die an einer masselosen, hookschen Feder befestigt ist und sich reibungslos bewegen kann.
• Die äußere Situation wird durch den Zusammenhang von Ort y und Kraft F gegeben. (Wo wirkt welche Kraft?)

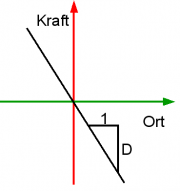
Bei einer hookschen Feder ist die Kraft proportional zur Auslenkung. Die Proportionalitätskonstante ist die Federhärte D. Die Rückstellkraft wirkt immer entgegen der Elongationsrichtung, es gilt also: [math] F=-Dy [/math].

• Wir suchen nun Bewegungen des Körpers in der Zeit, also den Zeit-Ort-Zusammenhänge y(t), die in diesem Kraftverlauf möglich sind.
• Die Lösung liefert uns das Newtonsche Axiom [math] F=\dot p = m a = m \ddot y[/math]. Es beschreibt nämlich den Zusammenhang zwischen Kraftverlauf und zeitlichen Ablauf der Bewegung!

Die Kraft hat man nun auf zwei Arten beschrieben. Einmal räumlich, abhängig vom Ort und zeitlich, abhängig von der Zeit und kann die beiden Ansätze gleichsetzen:

[math] m \,\ddot y = -D \,y[/math]

[math]\ddot y= -\frac{D}{m} \quad y  [/math]   Differentialgleichung (DGL) der harmonischen Schwingung

Wir suchen also Zeit-Orts-Gesetze, deren zweite zeitliche Ableitung ein Vielfaches von sich selbst sind!!

Ortsgesetze als Lösungen

Durch systematisches Probieren findet man Lösungen dieser DGL:

[math] y(t)=\hat y \,sin(\omega \,t)[/math] Schwingungen mit einer beliebigen Amplitude und Frequenz
[math] y(t)=\hat y sin(\omega t + \varphi_0)[/math] Schwingungen mit einer zusätzlichen Phasenverschiebung: 
[math] y(t) = 0[/math] Der Stillstand ist auch eine Lösung! 

Zur Begründung muss man die Ortsgesetze zweimal ableiten, z.B:

[math]\ddot y = -\hat y \,\omega^2 \,\sin(\omega t) =- \omega^2 \,y[/math]

Berechnung der Frequenz

Die Frequenz der Schwingung ergibt sich auch aus der DGL. Denn aus dem sinusförmigen Ansatz folgt:

[math]\ddot y =- \omega^2 \,y[/math] und vergleicht man dies mit der DGL:

[math]\ddot y= -\frac{D}{m} \, y [/math] , so folgt direkt:

[math]\omega^2= \frac{D}{m}[/math]  oder  [math]\omega= \sqrt{\frac{D}{m}}[/math]  ;  [math] f = \frac{1}{2\pi}\sqrt{\frac{D}{m}}[/math]  ;  [math] T =  2\pi \sqrt{\frac{m}{D}}[/math]   Frequenz einer harmonischen Schwingung, sie hängt nicht von der Amplitude ab!

Die Schwingungsdauer, bzw Frequenz folgt aus der Kreisfrequenz mit: [math] \omega=2\,\pi\, f [/math] und [math] T = \frac{1}{f}[/math]

Untersuchung dreier Schwingungen

• Ziel der Untersuchung ist es, das -Zeit-Orts-Gesetz [math] y(t)[/math] und damit auch die Frequenz der Schwingung aus der äußeren Situation, wie z.B. die Masse eines Körpers herzuleiten.

Dazu ist es sinnvoll jeweils die DGL aufzustellen. Zunächst muss man ein Koordinatensystem wählen und den Ort-Kraft-Verlauf bestimmen. Vor allem beim Fadenpendel hilft auch ein Blick in ein Buch oder ins Internet weiter.

Als Ergebnis sollen Sie sowohl eine allgemeine Formel erstellen, sowie eine konkrete Rechnung mit den gemessenen Größen durchführen.

• Welche Schlussfolgerung können Sie aus der allgemeinen Lösung ziehen? (Z.B. Abhängigkeit von der Masse, etc.)

• Vergleichen Sie dann die errechnete Frequenz mit der gemessenen und führen Sie eine Fehlerrechnung durch.

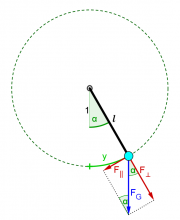
Das Fadenpendel

Fadenpendel mit wirkenden Kräften

[math] F_{II}=-mg*sin(\phi)[/math]

da: [math] y=\phi*l[/math]

[math] F_{II}=-mg*sin((1/l) * y)[/math]

[math] F_{II}=-m*\ddot y[/math]

[math] \ddot y=g*sin((1/l) * y)[/math]

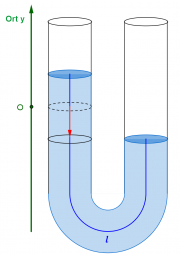
Schwingendes Wasser im U-Rohr

Versuchsaufbau: Schwingendes Wasser im U-Rohr

Der schematische Versuchsaufbau

Um die Amplitude in ein Koordinatensystem einzuzeichnen, nimmt man nur eine Seite des Schlauches und misst den Ausschlag s der Flüssigkeit aus der Ruhelage nach oben bezieghungsweise unten.

Vermutungen wovon die Frequenz abhängen könnte

• Wassermenge
• Rohrdicke
• Rohrkrümmung
• Rauigkeit
• Art der Flüssigkeit
• Amplitude

Aus den in der Differienzialgleichung verwendeten Faktoren lässt sich schließen, dass von diesen Vermutungen die Wassermenge und die Rohrdicke sowie zusätzlich die Erdbeschleunigung einen Einfluss auf die Frequenz nehmen. Ergebnis DGL: [math] y''=-2APg/m*y[/math]

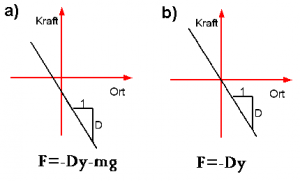
Federpendel im Gravitationsfeld

Versuchsaufbau Federpendel

Der Ursprung des Koordinatensystem entspricht bei a) dem Ende der entspannten Feder. Bei Abbildung b) entspricht der Ursprung der Ruhelage des Pendels. Sowohl bei a), als auch bei b), hängt die Masse m an der Feder

Daraus ergibt sich die Differentialgleichung zweiter Ordnung: [math] \ddot y=-D/my[/math] mit der Lsg: [math] \sin(\sqrt{D/m}t)[/math] woraus man auf die vollständige Zustandsvorschrift [math]y[/math] schliessen kann: [math] y=\hat y\sin(wt) \rightarrow y=\hat y\sin(\sqrt{D/m}t)[/math]