Die Energie des elektrischen Feldes: Unterschied zwischen den Versionen
(→Die Energiedichte des elektrischen Feldes) |
(→Energiedichte des elektrischen Feldes eines Kondensators) |
||
| Zeile 20: | Zeile 20: | ||
Die räumliche Änderung des Potentials ist daher auch konstant. Bei größerem Abstand steigt deswegen die Potentialdifferenz, also die Spannung: | Die räumliche Änderung des Potentials ist daher auch konstant. Bei größerem Abstand steigt deswegen die Potentialdifferenz, also die Spannung: | ||
| − | :<math>E = \varphi ' = \frac{U}{d} \quad \Rightarrow \quad U = E\, d </math> | + | :<math>E = \varphi ' = \frac{\Delta \varphi}{\Delta s} = \frac{U}{d} \quad \Rightarrow \quad U = E\, d </math> |
| − | Je kleiner der Plattenabstand ist, desto geringer ist die Spannung bei gleicher Ladungsmenge. Die Kapazität des Kondensators | + | Je kleiner der Plattenabstand ist, desto geringer ist die Spannung bei gleicher Ladungsmenge. Die Kapazität des Kondensators nimmt mit kleinerem Abstand zu, was man auch durch [[Der_Kondensator#Der_ideale_Kondensator|theoretische Überlegungen]] findet. |
Für das Auseinanderziehen der Platten ist Energie nötig, denn die Platten werden vom Feld zusammengezogen. Diese Energie steckt in dem immer größer werdenden Feld und kommt aus dem Menschen, der die Platten auseinanderzieht. Die Energiedichte beschreibt wieviel Energie pro Volumen im Feld gespeichert ist: | Für das Auseinanderziehen der Platten ist Energie nötig, denn die Platten werden vom Feld zusammengezogen. Diese Energie steckt in dem immer größer werdenden Feld und kommt aus dem Menschen, der die Platten auseinanderzieht. Die Energiedichte beschreibt wieviel Energie pro Volumen im Feld gespeichert ist: | ||
:<math> | :<math> | ||
\begin{array}{rcl} | \begin{array}{rcl} | ||
| − | \ | + | \rho_{el}&=& \frac{W}{V} \\ |
| − | + | &=& \frac{\frac{1}{2}C\,U^2}{A\,d}\\ | |
| − | + | &=& \frac{\frac{1}{2} \epsilon_0 \, \frac{A}{d}\, (E\,d)^2}{A\,d}\\ | |
| − | + | &=& \frac{\frac{1}{2} \epsilon_0 \, A\, E^2 d^2}{A\,d^2}\\ | |
| − | + | &=& \frac{1}{2} \epsilon_0 \, E^2 | |
\end{array} | \end{array} | ||
</math> | </math> | ||
| + | |||
| + | Das Endergebnis hängt nicht von Eigenschaften des Kondensators, wie Fläche oder Abstand, ab! Nur die Feldstärke spielt eine Rolle. Dies unterstützt nochmal die Behauptung, dass die Energie im Feld gespeichert wird. | ||
| + | |||
| + | In der Energiedichte spielt außerdem die Ausdehnung des Feldes keine Rolle, jedem beliebig kleinen Feldausschnitt kann man eine Energiedichte zuordnen. Deshalb ist der Zusammenhang von Feldstärke und Energiedichte auf jedes elektrische Feld, auch auf inhomogene Felder übertragbar. | ||
{|class="wikitable" style="border-style: solid; border-width: 4px " | {|class="wikitable" style="border-style: solid; border-width: 4px " | ||
| | | | ||
| − | Die Energiedichte | + | Die Energiedichte eines elektrischen Feldes<ref>Auch das Magnetfeld und das Gravitationsfeld haben eine Energiedichte: <br/><math>\rho_{mag} = \frac{1}{2} \mu_0 \, H^2 \text{ }</math> und <math>\text{ }\rho_{grav} = \frac{1}{2} \frac{1}{4\, \pi\, G} \, g^2</math> </ref> |
ist proportional zum Quadrat der Feldstärke: | ist proportional zum Quadrat der Feldstärke: | ||
:<math>\rho_{el} = \frac{W}{V} = \frac{1}{2} \epsilon_0 \, E^2</math> | :<math>\rho_{el} = \frac{W}{V} = \frac{1}{2} \epsilon_0 \, E^2</math> | ||
Version vom 3. Mai 2017, 11:46 Uhr
(Kursstufe > Das elektrische Feld)
Die Betrachtungen zur Energie des elektrischen Feldes führt man am Beispiel eines idealen Plattenkondensators durch. Dadurch sind die Ergebnisse auch auf alle homogenen Felder übertragbar. Bei inhomogenen Feldern muss man einen hinreichend kleinen Raumausschnitt wählen, in dem das Feld annähernd homogen ist.
Energiedichte des elektrischen Feldes eines Kondensators
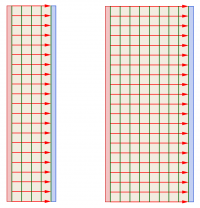
Versuch: Plattenabstand vergrößern bei konstanter Ladung
Ein Plattenkondensator wird z.B. mit einer geriebenen Schallplatte oder mit einem Hochspannungsnetzgerät auf 10kV aufgeladen und dann von der Spannungsquelle getrennt. Danach vergrößert und verkleinert man den Abstand der Platten.
- Beobachtung
Beim Auseinanderziehen der Platten steigt die Spannung an. Schiebt man die Platten wieder auf den ursprünglichen Abstand zusammen, so stellt sich auch die ursprüngliche Spannung wieder ein.
Video des Versuchs. (Uni Würzburg)
- Folgerung
Die Ladung pro Fläche und damit die Feldstärke ist konstant:
- [math]E = \frac{1}{\epsilon_0}\frac{Q}{A}[/math]
Die räumliche Änderung des Potentials ist daher auch konstant. Bei größerem Abstand steigt deswegen die Potentialdifferenz, also die Spannung:
- [math]E = \varphi ' = \frac{\Delta \varphi}{\Delta s} = \frac{U}{d} \quad \Rightarrow \quad U = E\, d [/math]
Je kleiner der Plattenabstand ist, desto geringer ist die Spannung bei gleicher Ladungsmenge. Die Kapazität des Kondensators nimmt mit kleinerem Abstand zu, was man auch durch theoretische Überlegungen findet.
Für das Auseinanderziehen der Platten ist Energie nötig, denn die Platten werden vom Feld zusammengezogen. Diese Energie steckt in dem immer größer werdenden Feld und kommt aus dem Menschen, der die Platten auseinanderzieht. Die Energiedichte beschreibt wieviel Energie pro Volumen im Feld gespeichert ist:
- [math] \begin{array}{rcl} \rho_{el}&=& \frac{W}{V} \\ &=& \frac{\frac{1}{2}C\,U^2}{A\,d}\\ &=& \frac{\frac{1}{2} \epsilon_0 \, \frac{A}{d}\, (E\,d)^2}{A\,d}\\ &=& \frac{\frac{1}{2} \epsilon_0 \, A\, E^2 d^2}{A\,d^2}\\ &=& \frac{1}{2} \epsilon_0 \, E^2 \end{array} [/math]
Das Endergebnis hängt nicht von Eigenschaften des Kondensators, wie Fläche oder Abstand, ab! Nur die Feldstärke spielt eine Rolle. Dies unterstützt nochmal die Behauptung, dass die Energie im Feld gespeichert wird.
In der Energiedichte spielt außerdem die Ausdehnung des Feldes keine Rolle, jedem beliebig kleinen Feldausschnitt kann man eine Energiedichte zuordnen. Deshalb ist der Zusammenhang von Feldstärke und Energiedichte auf jedes elektrische Feld, auch auf inhomogene Felder übertragbar.
|
Die Energiedichte eines elektrischen Feldes[1] ist proportional zum Quadrat der Feldstärke:
|
Fußnoten
- ↑ Auch das Magnetfeld und das Gravitationsfeld haben eine Energiedichte:
[math]\rho_{mag} = \frac{1}{2} \mu_0 \, H^2 \text{ }[/math] und [math]\text{ }\rho_{grav} = \frac{1}{2} \frac{1}{4\, \pi\, G} \, g^2[/math]