Messunsicherheit und Fehlerrechnung

Messfehler

• Jede Messung ist nur eine Annäherung an den wahren Wert einer Größe.
• Dabei entstandene Messfahler teilt man in systematische und zufällige Fehler ein. Bei zufälligen Fehlern geht man davon aus, dass die Messwerte um den korrekten Wert schwanken. Bei einem systematischen, z.B. durch einen falschen Versuchsaufbau verschieben sich die gemessenen Werte um einen Betrag. Sie sind schwer zu korrigiren. Zufällige Fehler werden durch Schwankungen der Messgröße, der Messgeräte, der Umwelt, durch den Beobachter etc. verursacht. Sie sind unvermeidbar, können aber abgeschätzt und durch Wiederholung verringert werden. Dazu verwendet man die Statistik. Graphische Veranschaulich der Fehlertypen.

Angabe von Messfehlern

• Als absolute Angabe mit Einheiten: [math]l=2m (\pm 0,01m)[/math]
• Als relative Angabe ohne Einheiten: [math]l=2m (\pm 0,05)(\pm 0,5%)[/math]
• Mit Hilfe von geltenden Ziffern, wobei nur die letzte Ziffer fehlerbehaftet ist: [math]l=2,000m[/math]

Statistische Beurteilung von zufälligen Fehlern

• Dazu müssen eine möglichst große Anzahl von Messungen der gleichen Größe [math]x[/math] durchgeführt werden.

Gaußsche Glockenkurve

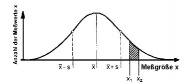
• Häufig kann man annehmen, dass die Messwerte normalverteilt sind, die Häufigkeiten also der Gaußschen Glockenkurve entsprechen.
• Der Verlauf der Kurve und damit die Messwerte werden durch die Angabe des Mittelwerts ([math]\bar x[/math]) und der Standardabweichung ([math]s[/math] oder [math]\sigma[/math]) vollständig festgelegt. Der Mittelwert gibt den Ort des Maximums an, die Standardabweichung gibt die Stellen der Wendepunkte an.

[math]\bar x = \frac{\sum_{i=1}^N x_i}{N} \qquad \sigma = s = \sqrt{\frac{\sum_{i=1}^N (\bar x - x_i)^2}{N-1}}[/math]

Gausskurve mit Vertrauengrenzen

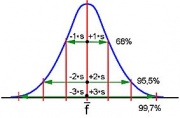
• Die Standardabweichung gibt an, wie genau die Messung ist. Kleine Abweichung = Genaue Messung. Man kann damit auch die Wahrscheinlichkeit angeben, dass der wahre Wert innerhalb dieses Bereichs liegt.

Maximale absolute Abweichung | Wahrscheinlichkeit
            s                |    68% (ca. 2/3)
          2 s                |    95%
        2,5 s                |    99%

Fehlerfortpflanzung

• Häufig werden eine oder mehrere fehlerbehaftete Ergebnisse verwendet, um ein Gesamterbegnis zu berechnen, das natürlich auch fehlerbehaftfet ist. Man spricht von Fehlerfortpflanzung.

Summen und Differenzen

• Die absoluten Fehler addieren sich.

Beispiel: Es wird die Dicke eines Blatt Papiers zu [math]0,2 mm (\pm 0,01mm)[/math] bestimmt. Für die Dicke von 50 Blättern ergibt sich: [math]10mm (\pm 0,5 mm)[/math]

Produkte und Quotienten

• Die relativen Fehler addieren sich.

Beispiel: Zur Bestimmung der Geschwindigkeit wurde die Strecke und die Zeit gemessen: [math]s = 5 m (\pm 0,01 m) (\pm 0,002) (\pm 0,2%)[/math]

[math]t = 2 s (\pm 0,1 s) (\pm 0,05) (\pm 5%)[/math]

[math]v=\frac{s}{t}= 2,5 m/s (\pm 0,052)(\pm 5,2%)[/math]

Aus dem relativen Fehler ist es nun auch möglich wieder den absoltuten Fehler zu berechnen.

Potenzen und Wurzeln

• Die relativen Fehler werden mit der Potenz gewichtet und addiert.

Beispiel: Bestimmung der Periodendauer eines Pendels.

[math]T = 2\Pi \frac{\sqrt{l}}{\sqrt{g}} = 2\Pi \frac{l^{1/2}}{g^{1/2}}[/math]

[math]l = 0,6m (\pm 0,1%)[/math]

[math]g = 9,81 m/s^2 (\pm 0,01%)[/math]

Die relativen Messfehler werden nun mit 1/2 gewichtet (multipliziert) und addiert:

[math]T = 1,5539 s (\pm 0,055%)[/math]

In diesem Fall ist also der Gesamtfehler kleiner als der größte Einzelfehler!