Der Hall-Effekt
(Kursstufe > Elektro-Magnetismus)
Die Drehzahl des Motors kann mit Hall-Sensoren berührungslos gemessen werden. (Video: Raddrehsensoren)
Wie schnell sind die Ladungsträger im Kabel? Und wieviele sind es? (Animation: Elektronenleitung und Löcherleitung
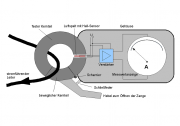
[1] Diese "Strommesszange" gestattet es berührungsfrei die Stärke von Gleichströmen zu messen. (Video: Anwendungsbeispiel)
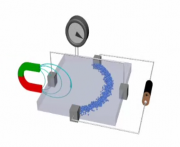
Animation zweier verschiedener Hallsonden
Inhaltsverzeichnis
Erklärung des Hall-Effekts mit der Lorentzkraft
Die gemessene Spannung läßt sich mit der Lorentzkraft auf die bewegten Ladungsträger erklären. Diese verschieben sich aufgrund der wirkenden Lorentzkraft quer zum Leiter. In den meisten Leitern, insbesondere in Metallen, sind die Ladungsträger die Elektronen.
Die Verschiebung der Elektronen verursacht andererseits ein elektrisches Feld, dass der Lorentzkraft entgegenwirkt. Deshalb stellt sich ein Gleichgewicht ein, bei dem die Lorentzkraft auf ein Elektron gleich der elektrischen Kraft ist.
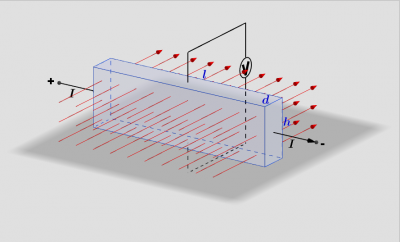
Diese Zeichnung zeigt das Plättchen im Magnetfeld. Durch die angelegte Spannung fließt ein Strom vom positiven Pol zum negativen Pol. Im Falle von Metallen sind die Ladungsträger negative Elektronen und bewegen sich vom Minus- zum Pluspol. Verwendet man p-dotierte Halbleiter, so wandern positive "Löcher" vom Plus- zum Minuspol.
Die Zeichnung kann mit der rechten Maustaste gedreht werden.
Berechnung der Hallspannung
Um den Zusammenhang zwischen Hallspannung, Magnetfeldstärke, Stromstärke und den Materialeigenschaften des Leiters zu untersuchen, macht man zwei Ansätze:
- Die Lorentzkraft auf die Ladungen ist gleich der elektrischen Kraft.
- Das elektrische Feld ähnelt dem eines Plattenkondensators.
- [math]F_E=F_L[/math]
Die Lorentzkraft auf ein Elektron[2] beträgt: [math]F_L =\mu_0\, e \, v \, H[/math] mit der Elementarladung [math]e[/math] eines Elektrons.
Die elektrische Kraft auf ein Elektron beträgt: [math]F_E = e \, E[/math].
[math] \begin{alignat}{2} e \, E &= \mu_0\, e \, v \, H & \quad |\,\mathopen: \, e \\ \Rightarrow \quad E &= \mu_0 \, v \, H \end{alignat} [/math]
Für die Feldstärke nimmt man einen Plattenkondensator mit dem Plattenabstand h an, also: [math]E=\frac{U_H}{h}[/math]
- [math]\frac{U_H}{h}= \mu_0 \, v \, H[/math]
(*) [math]U_H = \mu_0\, v \, H \, h[/math]
Die Hallspannung ist proportional zur Magnetfeldstärke (Flussdichte)
und zur Geschwindigkeit der Ladungsträger.
Die Hallspannung hängt nicht von der Ladungsmenge auf den Ladungsträgern ab.
Bis jetzt bleiben Materialeigenschaften unberücksichtigt. Das ändert sich, wenn man die Ladungsträgerdichte im leitenden Material betrachtet:
Die Kraft auf alle Elektronen im Leiter ist [math]F_{Lges}=\mu_0 \, H \, I \, l[/math]. Wenn man annimmt, dass sich die Anzahl von [math]N_q[/math][3] Elektronen im Leiter befindet, ergibt sich die Kraft auf ein Elektron als der [math]N_q[/math]-te Teil der gesamten Kraft:
- [math]F_E=F_L[/math]
(**) [math]e \frac{U_H}{h}=\mu_0 \ H \, I \, l \, \frac{1}{N_q}[/math]
Nach der Hallspannung auflösen:
- [math]U_H=\frac{\mu_0 \, H \, I \, l \, h}{N_q \, e}[/math]
Das Volumen beträgt [math]V=l\,h\,d,[/math] also ist [math]l\,h=\frac{V}{d}[/math].
- [math]U_H=\frac{\mu_0 \, H \, I}{d} \frac{V}{N_q} \frac{1}{e}[/math]
Die Anzahl der Ladungsträger pro Volumen [math]\rho_N=\frac{N_q}{V}[/math][4] heißt "Ladungsträgerdichte". Damit kann man das Ergebnis etwas kürzer schreiben:
(***) [math]U_H=\frac{\mu_0 \, H \, I}{d} \frac{1}{\rho_N\, e}[/math]
Der Bruch [math]\frac{1}{\rho_N\, e} = \frac{V}{N_q\,e}[/math] heißt Hallkonstante [math]R_H[/math] und ist eine Materialeigenschaft, die von der Ladungsträgerdichte abhängt. Sie ist gerade der Kehrwert der Ladungsdichte des Leiters. Je kleiner die Ladungsdichte, desto größer die Hallkonstante.
Ergebnisse
Hallsonde zur Messung der Feldstärke
Da die Hallspannung proportional zur Magnetfeldstärke ist, kann man die Feldstärke messen! Als Sonde dient ein stromdurchflossenes Leiterstück. Mit Hilfe des Magnetfeldes einer Spule kann man die Sonde eichen.
Abhängigkeit der Hallspannung
[math]U_H=R_H \, \frac{\mu_0 \, H \, I}{d} \quad \text{mit der Hallkonstante}\quad R_H = \frac{1}{\rho_N\, e} \quad \text{und der Ladungsträgerdichte}\quad \rho_N = \frac{N_q}{V}[/math]
Die Hallspannung ist proportional zur Magnetfeldstärke (Flussdichte) und zur Stromstärke,
antiproportional zur Dicke des Leitermaterials und zur Ladungsträgerdichte.
Um eine möglichst große Hallspannung in einem Magnetfeld zu erreichen, gibt es drei Möglichkeiten:
- Man verwendet eine hohe Stromstärke I. Das ist unpraktisch, weil sich der Leiter erwärmt und man viel Energie benötigt.
- Man verwendet einen Leiter mit geringer Dicke d.
- Man verwendet ein Material mit einer großen Hallkonstante. Dazu muss die Ladungsträgerdichte klein sein. Das ist einleuchtend, denn bei kleiner Ladungsträgerdichte müssen sich für den gleichen Strom die Ladungsträger schneller bewegen und so entsteht eine große Lorentzkraft auf die einzelnen Ladungsträger. In der Praxis verwendet man deshalb dotierte Halbleiter.
Vorzeichen der Ladungsträger
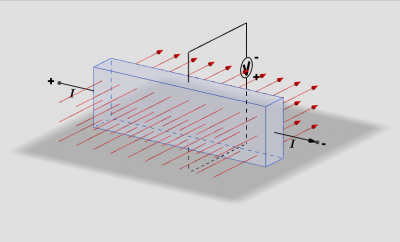
Vom Vorzeichen der Hallspannung kann man auf das Vorzeichen der Ladungsträger schließen. Hiermit kann man zeigen, dass in Metallen die Ladungsträger negativ sind und in p-dotierten Halbleitern positiv.
Geschwindigkeit der Ladungsträger
Ist die Feldstärke bekannt, so kann man die Geschwindigkeit der Ladungsträger, z.B. der Elektronen bestimmen. Dazu schreibt man die Gleichung (*) um:
- [math]v=\frac{U_H}{\mu_0 \, H \, h}[/math]
Anzahl der Ladungsträger pro Volumen
Auch die Anzahl der freien Ladungsträger kann mit diesem Versuch bestimmt werden! Dazu muss man nur (***) nach der Ladungsträgerdichte auflösen:
- [math]\rho_N=\frac{\mu_0 \, H \, I}{U_H \, d \, e}[/math]
Die einfache Messung von diesen makroskopischen Größen läßt es also zu auf atomare Eigenschaften des Leiters zu schließen! Kennt man noch das Molgewicht des Leiters, so kann man z.B. auf die Anzahl der freien Elektronen eines Metalls schließen!
Zwei beispielhafte Werte für ein Metall und einen Halbleiter:
Material Hall-Konstante
[math]\frac{V}{N_q\,e}[/math]Ladungsdichte
[math]\frac{N_q\,e}{V}[/math]Ladungsträgerdichte
[math]\frac{N_q}{V}[/math]molare Ladungsträgerdichte
[math]\frac{N_q}{n}[/math]Kupfer [math]-50\cdot 10^{-6}\,\rm\frac{{cm}^3}{C}[/math] [math]-20000\,\rm\frac{C}{{cm}^3}[/math] [math]1{,}25\cdot10^{23}\,\rm\frac{1}{{cm}^3}[/math] [math]8{,}9\cdot10^{23}\,\rm\frac{1}{mol}[/math] Germanium
p-dotiert[math]5000\,\rm\frac{{cm}^3}{C}[/math] [math]0{,}2\cdot10^{-3}\,\rm\frac{C}{{cm}^3}[/math] [math]1{,}25\cdot10^{15}\,\rm\frac{1}{{cm}^3}[/math] [math]1{,}7\cdot10^{16}\,\rm\frac{1}{mol}[/math]
Das Kupfer hat also pro Volumen viel bewegliche Ladung zur Verfügung, das dotierte Germanium um den Faktor [math]10^8[/math] weniger!
Ein mol eines Stoffes enthält ca. [math]6\cdot 10^{23}[/math] Atome. Das heißt, bei Kupfer stellt jedes Atom ungefähr ein Elektron zum Ladungstransport zur Verfügung. Beim Germanium ist nur eines von 35 Millionen Atomen dotiert und stellt ein "Loch" zum Ladungstransport.
Versuch: Messen der Hall-Spannung
Aufbau und Durchführung
Ein dünnes Silberband befindet sich in einem Magnetfeld. Senkrecht zu den magnetischen Feldlinien läßt man einen Strom durch das Band fließen. Senkrecht zu Strom- und Magnetfeldlinienrichtung misst man die Spannung zwischen oberem und unterem Rand des Silberbandes.
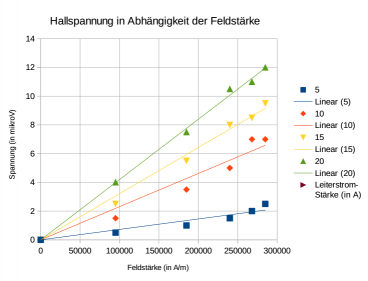
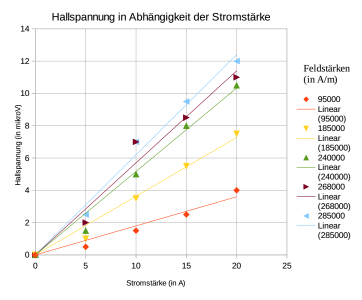
Die Spannung misst man in Abhängigkeit von der magnetischen Feldstärke und der Stromstärke.
Da die zu messenden Spannungen sehr klein sind, muss man vor das eigentliche Voltmeter einen Messverstärker schalten.
Zur Variierung des Magnetfeldes kann man einen Elektromagneten verwenden oder verschiedene Festmagnete mit unterschiedlichen Feldstärken.
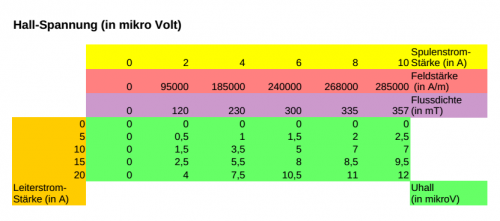
- Messung der Hall-Spannung
Verwendet man einen Elektromagneten, kann man durch die Spulenstromstärke die magnetische Feldstärke variieren. Der Elektromagnet sollte kalibiert sein, das heißt, man muss den Zusammenhang zwischen Spulenstromstärke und Feldstärke kennen.
- Zu Beginn der Messung wird der Eisenkern des Elektromagneten entmagnetisiert und der Spulenstrom ausgeschaltet.
- Dann stellt man den Strom durch das Silberband auf den gewünschten Wert ein und nimmt mit den Reglern am Hall-Effekt-Gerät und am Messverstärker einen Nullabgleich der Spannung vor. (Stellt die Anzeige auf Null.)
- Jetzt wird der Spulenstrom und damit die magnetische Feldstärke schrittweise auf die gewünschten Werte erhöht.
Will man die Messung für eine weitere Stromstärke machen, so wiederholt man diese Prozedur.
Beobachtung und Messung
- Vorzeichen der Hall-Spannung
Fließt durch das Silberband ein Strom, so kann man zwischen oberem und unteren Rand eine kleine Spannung messen. Die Polung der Spannung kann man der Zeichnung entnehmen. Ändert man die Richtung des Stromes oder der Feldstärke, so kehrt sich auch das Vorzeichen der Spannung um.
Fußnoten
- ↑ Mit freundlicher Genehmigung der CHAUVIN ARNOUX GmbH
- ↑ Hierbei nimmt man an, dass die Ladungsträger im Leiter jeweils eine Elementarladung tragen. Man kann aber auch annehmen, dass die Ladungsträger mehr oder weniger Ladung tragen, die nachfolgende Rechnung ändert sich dadurch nicht, denn die Ladung eines Ladungsträgers kürzt sich aus der Rechnung raus.
- ↑ Es ist üblich Teilchenzahlen mit einem großen N abzukürzen und die Stoffmenge mit einem kleinen n.
- ↑ Die Ladungsträgerdichte wird oft mit einem kleinen n abgekürtzt. Allerdings ist dies auch die Abkürzung der Stoffmenge. Die Abkürzung [math]\rho[/math] wird allgemein für verschiedene Dichten, wie die Masendichte oder die Ladungsdichte verwendet, der Index N weist hier auf die Teilchenanzahl hin. (Vgl. engl. Wikipedia: Number density)
Links
- Applet zur Elektronenbewegung in Metallen (F. Eschen vom Gymnasium Ybbenbüren)
- Wikipedia: dotierte Halbleiter
- Video: Messen der Driftgeschwindigkeit in Halbleitern, youtube: "Minority Carriers" (Haynes & Shockley)
- Animation des Halleffekts (Matthias Hornof)
- Video: Überprüfung von aktiven und passiven Raddrehzahlsensoren (von "OSZLausitzKfz")
- Video: Anwendungsbeispiel Stromzange ("32223L - Digital- Zangen-Multimeter" von "swstahlvideos")
- Animation: Elektronenleitung (LEIFI)
- Animation: Löcherleitung (LEIFI)
- Experimente mit dem Magnetfeldsensor eines Handys und anderen externen Sensoren (Patrick Bronner, Friedrich-Gymnasium Freiburg / mascil project)
- Smartphone im Physikunterricht Hier werden unter anderem die Funktionsweise der Sensoren und auch eines Magnetfledsensors erklärt. (Prof. Dr. Franz Eisele, Physikalisches Institut der Universität Heidelberg)