Die magnetische Feldstärke

(Kursstufe > Elektro-Magnetismus)

Bei der Festlegung der Feldstärke verfolgt man einen deduktiven Ansatz. Die theoretische Definition läuft ganz parallel zu den anderen Feldstärken, als Kraft pro magnetische Probeladung.

$$\vec H = \frac{\vec F}{Q_m} \qquad [ H]=\rm \frac{1\, N}{1\,Wb}$$

Da man die magnetische Ladung nicht direkt messen kann, muss man diese Formel als Definition der magnetischen Ladung interpretieren:

$$Q_m = \frac{\vec F}{\vec H}$$

Die magnetische Feldstärke wird mit Hilfe eines Spulenfeldes definiert:

Eine Spule mit 1000 Windungen, durch die ein Strom von 1 mA fließt, ein Meter lang ist und möglichst dünn ist, hat im Inneren ein Feld der Stärke 1 A/m.

Magnetfeld einer schlanken Spule

Grundlage dieser Definition ist das Magnetfeld einer "schlanken" Spule. Als solche bezeichnet man eine Spule, die im Vergleich zum Spulendurchmesser relativ lang ist. Exakt stimmen die folgenden Überlegungen nur für eine unendlich lange, bzw unendlich dünne Spule.

Bei einer "schlanken" Spule befindet sich das homogene Feld ausschließlich im Innern der Spule. (Vgl. Feld einer Spule.)

• Der Spulendurchmesser spielt keine Rolle für die Feldstärke, da die Spule "unendlich" lang ist.

Die Spulen A und B werden ineinander (1) und hintereinander (2) geschoben.

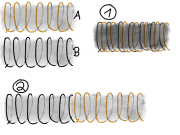
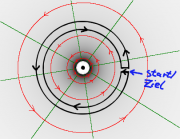
Setzt man zwei gleiche Spulen mit der gleichen Stromstärke zu einer Spule zusammen, so kann man daraus weitere Zusammenhänge herleiten. (Siehe Bild) Schiebt man die Spulen A und B ineinander (1), so addieren sich die Feldstärken vektoriell, die Feldstärke verdoppelt sich also. Das kann nur an der doppelten Windungszahl n liegen. Fasst man je zwei Windungen zu einer zusammen, so kann man das auch als eine Verdoppelung der Stromstärke interpretieren:

• Die Feldstärke ist proportional zur Stärke des fließenden Stromes: $$H \sim I$$ und zur Anzahl der Windungen: $$H \sim n$$ .

Setzt man die Spulen A und B stattdessen hintereinander (2), so ändert sich die Feldstärke nicht! Aber die Anzahl der Windungen ist verdoppelt worden. Dies wird offensichtlich durch die Verdopplung der Länge ausgeglichen.

• Die Feldstärke ist antiproportional zur Länge der Spule: $$H \sim \frac{1}{l}$$ .

Deshalb kann man die magnetische Feldstärke festlegen, als:

$$H=\frac{n \, I}{l} \qquad [H]= \mathrm{\frac{1\,A}{1\,m}}$$ Magnetische Feldstärke einer "schlanken" Spule der Länge $$l$$ .

Man kann

$$n \, I$$ als Gesamtstromstärke durch den Schnitt der Spule sehen und den Quotienten mit der Länge als Stromstärkedichte. Kurz gesagt ist die Feldstärke der Spule gerade deren Stromstärkedichte.

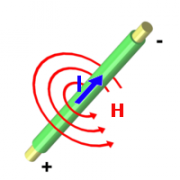
Feldstärke um ein Kabel

Mit Hilfe der Definition ist es auch möglich Messgeräte zur Feldstärkemessung zu bauen. Allerdings wird dies nicht gemacht, denn es ist umständlich. Meistens wird das Feld mit einer Hall-Sonde vermessen, deren Wirkung auf dem Hall-Effekt beruht.

Misst man mit einer solchen Hall-Sonde die Stärke des Magnetfeldes eines stromdurchflossenen Kabels, so stellt man fest:

Die Feldstärke nimmt antiproportinal zum Abstand r vom Kabel ab und ist proportional zur Stromstärke:

$$H=\frac{I}{2 \, \pi \, r}$$

Maxwellsche Formulierung

Die Gesetze für die Feldstärke von Spule und Kabel sind ähnlich aufgebaut. Das liegt an der gemeinsamen Grundlage der beiden Formeln.

Im Falle des Kabels ist

$$\mathrm{2 \, \pi \, r}$$ gerade die Länge einer Feldlinie um das Kabel herum. Man kann also schreiben:

$$H=\frac{I}{l}$$ bzw. $$H \, l = I$$

Das Produkt von Feldstärke und Feldlinienlänge ist gerade die Stromstärke!

Diese Erkenntnis ist verallgemeinerbar und ein Teil der vierten Maxwellschen Gleichung:

Ampèrsches Gesetz: Geht man irgendeinen geschlossenen Weg der Länge $$l$$ in einem Magnetfeld ab, so gilt $$\bar H \, l = I$$ . Dabei ist $$\bar H$$ die mittlere Feldstärke parallel zum Weg und $$I$$ die Stärke des Stroms senkrecht durch die vom Weg aufgespannte Fläche.

Kennt man die Feldstärke, so kann man also durch "Herumlaufen" in einem Magnetfeld herausbekommen wieviel Strom durch diesen geschlossenen Weg fließt! Wenn man die Stromstärke kennt, so ist die mittlere Feldstärke berechenbar! Diese Methode ist sehr ähnlich wie bei der Betrachtung der Ladung als Quelle von Feldern. Wobei bei der Quellenstärke geschlossene Flächen und keine geschlossenen Wege betrachtet werden.

Beispiele

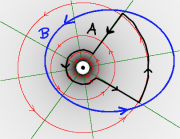
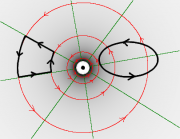
Bei Weg A geht man bei den Kreisbögen parallel zur Feldlinienrichtung, der Beitrag ist daher positiv. Bei den orthogonalen Teilwegen ist der Beitrag Null. Bei Weg B erhält man das gleiche Ergebnis wie bei Weg A, nämlichen den (positiven) Strom I.
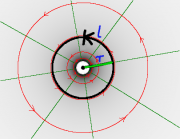
Bei diesem Weg ist die mittlere Feldstärke Null, denn man geht einmal parallel zur Feldlinienrichtung und einmal antiparallel. Daher erhält man korrekt, dass durch den Weg kein Strom fließt!
Auch hier fließt durch die beiden Wege kein Strom, die mittlere Feldstärke ist Null.

Herleitung der Spulenfeldstärke

Durch den geschlossenen Weg verlaufen vier Kabel, durch die der Strom in die Zeichenebene hineinfließt.

Eine Spule soll n Windungen haben, die von einem Strom der Stärke I durchflossen werden.

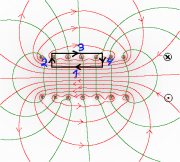
Um die Feldstärke des Magnetfeldes im Innern einer Spule abzuleiten, muss man sich geschickt einen geschlossenen Weg durch das Feld wählen. Man wählt einen rechteckigen Weg, der aus vier Teilwegen besteht. Für jeden der vier Teilwege bestimmt man das Produkt aus Feldstärke und Weglänge:

Bei Teilweg 1 herrscht die gesuchte Feldstärke H:

$$H \cdot l_1$$

Die Feldstärke von Teilweg 2 und 4 ist orthogonal zum Weg, der zum Weg parallele Anteil verschwindet:

$$0 \cdot l_2 + 0 \cdot l_4$$

Auf dem Teilweg 3 kann man die Feldstärke näherungsweise vernachlässigen, weil sich das Feld vor allem in der Spule befindet:

$$0 \cdot l_3$$

Somit ergibt sich insgesamt:

$$H \cdot l_1 + 0 \cdot l_2 + 0 \cdot l_4 + 0 \cdot l_3 = H \cdot l_1$$

Gehen durch die vom geschlossenen Weg aufgespannte Fläche

$$n_1$$ Windungen, durch die ein Strom der Stärke $$I$$ fließt, so ergibt sich:

$$H=\frac{n_1 \, I}{l_1}$$

Eine Spule ist normalerweise gleichmäßig gewickelt und deshalb ist das Verhältnis von Windungsanzahl zur Länge immer gleich:

$$H=\frac{n \, I}{l}$$