Der elektrische Schwingkreis
(Kursstufe > Elektromagnetische Schwingungen und Wellen)
Der analoge Synthesizer "Mini Moog" (Video)
Eine Induktionsschleife registriert die vorbeifahrenden Fahrzeuge.
Inhaltsverzeichnis
Versuch: Entladen eines Kondensators über eine Spule
Aufbau:

a) Der Anlasskondensator[2] ([math]C = 40\,\rm \mu F[/math]) eines Autos wird mit 15V bis 30V geladen und über verschiedene Widerstände oder ein Lämpchen (3,8V/0,07A) entladen. Dabei wird die Spannung am Kondensator und die Stärke des Entladungsstroms gemessen.
b) Der Kondensator wird über eine Spule ([math]L \approx 500\,\rm H[/math]) entladen.
c) Es werden vier Kondensatoren parallel geschaltet und der Versuch mit der Spule wiederholt.
d) Es wird eine Spule mit geringerer Induktivität verwendet.
Beobachtung:
a) Die Spannung nimmt ab, bis der Kondensator vollständig entladen ist. Der Abfall der Spannung hängt direkt mit der Stromstärke zusammen.
Die Spannung fällt zunächst schnell ab, dann immer langsamer. Je größer der Widerstand, desto langsamer entlädt sich der Kondensator.
b) Die Spannung nimmt periodisch negative und positive Werte an. Die Maximalwerte gehen schließlich auf Null zurück.
Die Stromstärke ist dann besonders groß, wenn die Spannung gerade Null ist.
Die Stromstärke ist positiv, wenn die Spannung sinkt.
c) Die Schwingung der Spannung hat eine kleinere Frequenz.
d) Die Schwingung hat eine größere Frequenz.
Erklärung
a) Je größer die antreibende Spannung und je kleiner der Widerstand, desto größer ist auch der Strom. Nach dem Ohmschen Gesetz gilt: [math]I=\frac{1}{R}\, U[/math].
Die Energie des geladenen Kondensators wird benötigt, um den Widerstand zu erwärmen. Dabei ensteht Entropie.
b) Die Spannung des Kondensators treibt einen Strom an, der in der Spule ein Magnetfeld aufbaut, bzw. den Eisenkern magnetisiert. Die Spule "bremst" dabei den Vorgang durch Selbstinduktion, sodass der Kondensator nicht schlagartig entleert wird.
Ist der Kondensator entladen, so sinkt die Stromstärke und das Magnetfeld (die Magnetisierung) nimmt ab. Durch die Selbstinduktionsspannung treibt nun die Spule den Strom weiterhin an und lädt den Kondensator mit der entgegengesetzten Polung wieder auf.
Die Energie des elektrischen Feldes im Kondensator fließt also ständig in das Magnetfeld (die Magnetisierung) und wieder zurück in das elektrische Feld.
In diesem Applet von Walter Fendt kann man den Vorgang sehr schön verfolgen.
c) Durch die Parallelschaltung vergrößert sich die Kapazität auf das Vierfache. Bei der gleichen Spannung wird also die vierfache Ladung gespeichert. Offenbar dauert der Lade- und Entladevorgang nun länger.
d) Durch die geringere Induktivität sinkt die Wirkung der Selbstinduktion und somit die "Bremswirkung" der Spule. Durch die größere Stromstärke geht der Lade- und Entladevorgang nun schneller.
Vergleich mit mechanischen Schwingungen
Elektromagnetische und mechanische Schwingungen weisen sehr große Parallelen auf. Sämtliche Erkenntnisse der mechanischen Schwingungen sind bis ins Detail übertragbar!
- Energiezufuhr bei Schwingungen
- Untersuchung einer harmonischen Federschwingung
- Beschreibung einer harmonischen Schwingung mit der Zeigerdarstellung
- Die Bewegungsgesetze einer harmonischen Schwingung
- Beschreibung einer harmonischen Schwingung mit einer Differentialgleichung
- Untersuchung von Schwingungen mit der Differentialgleichung
- Überlagerung von harmonischen Schwingungen
- Gedämpfte Schwingungen
- Energiezufuhr bei Schwingungen
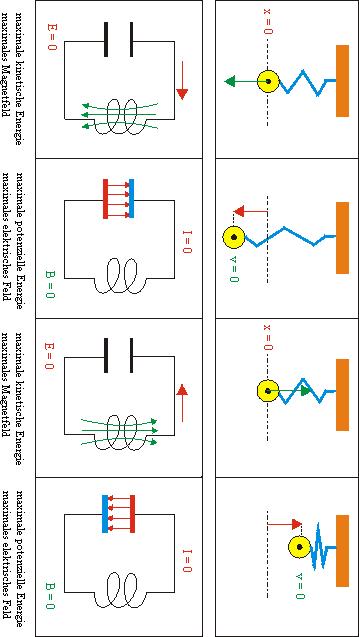
Hier kann man den Schwingungsvorgang vergleichen, dabei ist zu beachten, dass man sich das Federpendel am besten horizontal vorstellt, denn sonst kommt die Lageenergie im Schwerefeld noch hinzu, was die Situation verfälscht. Die Beschriftung ist deswegen schlecht zu lesen. (von LEIFI Physik)
Diese Tabelle stellt die sich entsprechenden Größen eines Federpendels und des elektromagnetischen Schwingkreises gegenüber. Es gibt verschiedene Möglichkeiten sich entsprechende Größen zu finden. Hier entspricht die Auslenkung des Pendels der Ladung des Kondensators und die Trägheit des Pendelkörpers der Induktivität der Spule. Die DGL des Schwingkreises wird durch einen Vergleich der Spannung an Spule und Kondensator gewonnen.
[3]
| Federschwingung | elektromagnetische Schwingung | |||||||
| Auslenkung | [math]y[/math] | [math]Q[/math] | verschobene Ladung im Kondensator | |||||
| [math]v=[/math] | [math]\dot y[/math] | Geschwindigkeit | [math] v[/math] | [math]I[/math] | Stromstärke | [math] I=[/math] | [math]\dot Q[/math] | |
| [math]a=[/math] | [math]\ddot y[/math] | Beschleunigung | [math]a[/math] | [math]\dot I[/math] | Änderung der Stromstärke | [math]\dot I=[/math] | [math]\ddot Q[/math] | |
| Rückstellkraft | [math]F[/math] | [math]U[/math] | Spannung am Kondensator | |||||
| [math]F=[/math] | [math]-D\,y[/math] | Federstärke | [math]D[/math] | [math]\frac{1}{C}[/math] | Kehrwert der Kapazität | [math]U=[/math] | [math]-\frac{1}{C}\,Q[/math] | |
| [math]F=[/math] | [math]m\, a[/math] | träge Masse | [math] m[/math] | [math] L[/math] | Induktivität der Spule | [math]U=[/math] | [math]L\, \dot I[/math] | |
| [math]p =[/math] | [math]m\, v[/math] | Impuls | [math] p[/math] | [math] n\, \Phi[/math] | n-facher magnetischer Fluss der Spule | [math]n\, \Phi =[/math] | [math] L\, I[/math] | |
| [math]F=m\, \ddot y =[/math] | [math] - D\, y[/math] | DGL | [math]y[/math] | [math]Q[/math] | DGL | [math]- L\, \ddot Q =[/math] | [math] \frac{1}{C} Q = U[/math] | |
| [math]\omega^2 =[/math] | [math] \frac{D}{m}[/math] | Frequenz | [math]\omega=2\, \pi\, f[/math] | Frequenz | [math]\omega^2 =[/math] | [math] \frac{1/C}{L} [/math] | [math] \left[= \frac{1}{L\, C}\right][/math] | |
| [math]E=[/math] | [math]\frac{1}{2} \, D y^2[/math] | Spannenergie | [math]E_{sp}[/math] | [math]E_{el}[/math] | elektrische Energie | [math]E=[/math] | [math]\frac{1}{2} \, \frac{1}{C}\,Q^2 [/math] | [math] \left[=\frac{1}{2} \, C U^2\right][/math] |
| [math]E=[/math] | [math]\frac{1}{2} \, m v^2[/math] | Bewegungsenergie | [math] E_{kin}[/math] | [math]E_{mag}[/math] | magnetische Energie | [math]E=[/math] | [math]\frac{1}{2} \, L I^2[/math] |
Unterteilung von Schwingungen nach Energieaspekten
Wie bei den mechanischen Schwingungen auch, kann man je nach Art der Energieabfuhr und Zufuhr verschiedene Fälle unterscheiden. (Vgl. Energiezufuhr bei Schwingungen)
- Gedämpfte oder Ungedämpfte Schwingung
- Durch den Widerstand der Kabel strömt bei einer gedämpften Schwingung Energie aus dem Schwingkreis, die Kabel werden erwärmt. Alle realen Schwingkreise sind gedämpft.
- Angeregte Schwingung
- Durch die Zufuhr von Energie in der Eigenfrequenz des Systems gleicht man die Dämpfung aus und simuliert eine ungedämpfte Schwingung. Es gibt verschiedene Schaltungen, mit denen man die Energiezufuhr steuern kann.
- Erzwungene oder freie Schwingung
- Bei einer erzwungenen Schwingung gibt man die Frequenz der Schwingung von Außen z.B. durch Anlegen einer Wechselspannung vor.
- Selbsterregte Schwingung
- Die Steuerung der Energiezufuhr geschieht durch das elektromagnetische System selbst. Rechnet man, ähnlich wie bei einer Pendeluhr, die Steuerung eines Schwingkreises noch zu dem System dazu, so genügt in diesem Fall das Anlegen einer konstanten Spannung und das System schwingt.
Links
- Applet von Walter Fendt
- Elektrischer Schwingkreis kompletter Versuch (youtube-Kanal physiksaal, Sven H. Pfleger, Neunkirchen)
- LEIFI: DGL von Schwingungen und Vergleich mit mechanischen Schwingungen
- LEIFI: Versuche zu elektromagnetischen Schwingungen
- Video: Jimmy Smith - Midnight Special (Jimmy Smith plays The Organ Grinder's Swing on the Hollywood Palace show aired October 2, 1965. Hosted by Fred Astaire.)
Fußnoten
- ↑

- ↑ Der Kondensator muss ungepolt sein, dass heißt er muss in verschiedene Richtungen aufladbar sein. Ein Elektrolytkondensator ist ungeeignet.
- ↑
Eine weitere Möglichkeit ergibt sich aus den Erhaltungsgrößen der Schwingung. Außer der Energie sind dies bei der mechanischen Schwingung der Impuls und beim elektro-magnetischen Schwingkreis die elektrische Ladung. Dieser Vergleich paßt auch in den Rahmen eines erweiterten Energiekonzeptes von Energieträgern und Potentialen. Der Geschwindigkeit entspricht, als Potential des Impulses, dem Potential der Ladung, also der Spannung. Der trägen Masse als "Impulskapazität" entspricht dann der "Ladungskapazität" des Kondensators. Die DGL des Schwingkreises wird mit einem Vergleich der Stromstärke durch Spule und Kondensator gewonnen.
Federschwingung elektromagnetische Schwingung Auslenkung [math]y[/math] [math] n\, \Phi[/math] n-facher magnetischer Fluss der Spule [math]n\, \Phi =[/math] [math] L\, I[/math] [math]v=[/math] [math]\dot y[/math] Geschwindigkeit [math] v[/math] [math]U[/math] Spannung an der Spule [math]U=[/math] [math]n\, \dot \Phi[/math] [math]a=[/math] [math]\ddot y[/math] Beschleunigung [math]a[/math] [math]\dot I[/math] Änderung der Spannung [math]\dot U=[/math] [math]n\, \ddot \Phi[/math] Rückstellkraft [math]F[/math] [math]I[/math] Stromstärke [math]F=[/math] [math]-D\,y[/math] Federstärke [math]D[/math] [math]\frac{1}{L}[/math] Kehrwert der Induktivität [math]I=[/math] [math]-\frac{1}{L}\,n\,\Phi[/math] [math]F=[/math] [math]m\, a[/math] träge Masse [math] m[/math] [math] C[/math] Kapazität des Kondensators [math]I=[/math] [math]C\, \dot U[/math] [math]p =[/math] [math]m\, v[/math] Impuls [math] p[/math] [math]Q[/math] verschobene Ladung im Kondensator [math]Q=[/math] [math]C\, U[/math] [math]F=m\, \ddot y =[/math] [math] - D\, y[/math] DGL [math]y[/math] [math]n\,\Phi[/math] DGL [math]C\,n\,\ddot \Phi =[/math] [math] - \frac{1}{L} n\,\Phi = I[/math] [math]\omega^2 =[/math] [math] \frac{D}{m}[/math] Frequenz [math]\omega=2\, \pi\, f[/math] Frequenz [math]\omega^2 =[/math] [math] \frac{1/C}{L} [/math] [math] \left[= \frac{1}{L\, C}\right][/math] [math]E=[/math] [math]\frac{1}{2} \, D y^2[/math] Spannenergie [math]E_{sp}[/math] [math]E_{mag}[/math] magnetische Energie [math]E=[/math] [math]\frac{1}{2} \, \frac{1}{L}(n \Phi)^2[/math] [math]\left[=\frac{1}{2} L\, I^2\right][/math] [math]E=[/math] [math]\frac{p^2}{2\,m}[/math] Bewegungsenergie [math] E_{kin}[/math] [math]E_{el}[/math] elektrische Energie [math]E=[/math] [math]\frac{Q^2}{2 C}[/math] [math]\left[=\frac{1}{2} \, C U^2\right][/math]