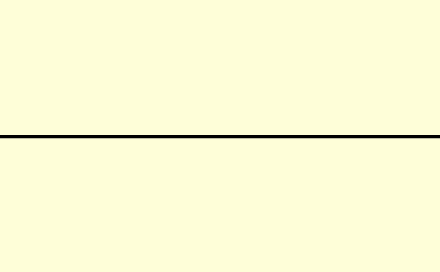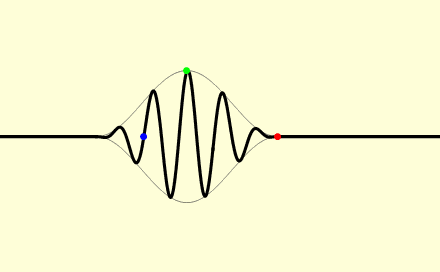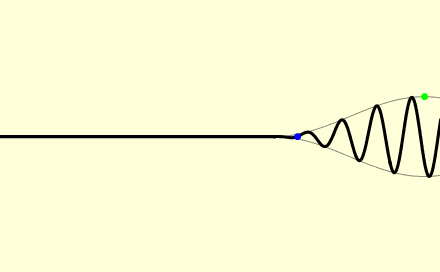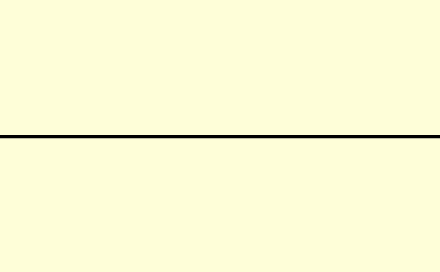Die Ausbreitungsgeschwindigkeit einer Welle

(Kursstufe > Mechanische Wellen)

Am Beispiel der La Ola-Welle wird klar, wovon die Ausbreitungsgeschwindigkeit abhängt. Sie ist dann schnell, wenn die NachbarIn schnell reagiert.

Die Reaktionszeit hängt zunächst nicht von der Amplitude ab, also wie hoch die Arme bewegt werden und auch nicht von der Frequenz, also wie schnell die Arme bewegt werden.

Für eine harmonische Welle hängt die Ausbreitungsgeschwindigkeit nur von der Kopplungsstärke der Schwingungen ab, nicht von Amplitude und Frequenz.

Für den Schall bedeutet das: Laute Töne (große Amplitude) sind so schnell wie leise und hohe Töne (große Frequenz) so schnell wie tiefe.

Dies stimmt aber nicht exakt. Beim genauen Hinhören stellt man fest, dass hohe Töne schneller sind als tiefe. Dies ist bei einem Donner gut zu hören oder beim Anschlagen einer Metallfeder. ("Star Wars-Effekt") Diesen Effekt nennt man Dispersion. Er tritt auch bei Lichtwellen auf.

Daraus kann man folgern, dass die Schwingungen der Wellen nicht harmonisch sind!

Versuch: Ausbreitungsgeschwindigkeit einer Wasserwelle (Wellenwanne)

Aufbau

Beobachtung

Messung der Geschwindigkeit mit Handstoppuhr

Weglänge s=20cm
10Hz
Zeit (in s) 1,09 1,09 1,13 1,00
20Hz
Zeit (in s) 1,00 1,09 0,97 1,00
30Hz
Zeit (in s) 1,06 1,07 1,12 1,06

Zusammenhang von Wellenlänge, Frequenz und Phasengeschwindigkeit

So sieht die La Ola-Welle nach 10 Sekunden aus. Person A hört gerade auf die Arme zu bewegen, Person J fängt gerade an.

An einem Beispiel: Bei der La Ola-Welle benötigt eine Person (A) zwei Sekunden um die Hände einmal nach oben dann nach unten und wieder in die Mitte zu bewegen. Das entspricht einer Schwingung mit der Periodendauer [math]T=2\,\rm s[/math]. In dieser Zeit hat sich die Welle um zehn Meter ausgebreitet, was genau der Wellenlänge [math]\lambda=10\,\rm m[/math] entspricht. Dementsprechend beträgt die Phasengeschwindigkeit

[math]c=\frac{10\, \rm m}{2\, \rm s}=5 \frac{\rm m}{\rm s}[/math]

Die Frequenz, mit der die Arme bewegt werden beträgt [math]f=\frac{1}{T}=0{,}5\,\rm Hz[/math], also eine halbe Schwingung pro Sekunde. Deshalb breitet sich die Welle pro Sekunde um eine halbe Wellenlänge aus:

[math]c=10\, \rm m\cdot 0{,}5\,\rm Hz = 5 \frac{\rm m}{\rm s}[/math]

[math]c= \frac{\lambda}{T} = \lambda \ f[/math] Phasengeschwindigkeit c einer Welle der Frequenz f und Wellenlänge [math]\lambda[/math].

Beispielrechnung

• Die Schallwellenlänge bei einem hohen und tiefen Ton. (1000 Hz und 100 Hz)

Die Schallgeschwindigkeit beträgt ca. 340 m/sec. Also folgt für die Wellenlänge:

[math]\lambda = \frac{c}{f} = \frac{340 \, \rm \frac{m}{s} }{1000 \, \rm \frac{1}{s}} = 0{,}34 \,\rm m[/math]

bzw: [math]\frac{340 \, \rm \frac{m}{s}}{100 \, \rm \frac{1}{s}} = 3{,}4 \,\rm m[/math]

Die kleinere Wellenlänge des höheren Tons ist der Grund warum kleine Flöten oder Pfeifen auch einen hohen Ton produzieren.

Gruppengeschwindigkeit

• In dem Bild dieses Wellenzugs ist deutlich zu sehen, dass die Gruppengeschwindigkeit (roter und grüner Punkt) hier größer ist als die Phasengeschwindigkeit (blauer Punkt).

• In diesem Applet kann man ein Wellenpaket simulieren, dass beliebig einstellbare Phasen- und Gruppengeschwindigkeiten hat.

Links

• Wikipedia: Gruppengeschwindigkeit
• Applet zur Phasen und Gruppengeschwindigkeit (Technische Universität Berlin; Numerische Fluiddynamik, Applets und Animationen)

• Video: WDR Planet Schule: Schallparade

• Bestimmung der Ausbreitungsgeschwindigkeit von Wasserwellen Andreas Schwabe, Carolin Rödel, Christiane Wagner, Friedrich Heberlein, Sebastian Bauerschmidt, Tobias Bierlein, Holger Rupp, 23. Januar 2006