Masse & Impuls von Photonen - Der Compton-Effekt

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche

(Kursstufe > Licht als Teilchen)

Wenn Licht, wie man beim Photoeffekt gesehen hat, als Teilchen zu beschreiben ist, dann müßte es eigentlich noch mehr Teilcheneigenschaften haben. Welche typischen Teilcheneigenschaften hat denn z.B. ein Elektron oder eine Billiardkugel?

Insbesondere haben alle Materieteilchen eine Masse, dass heißt, sie sind haben eine Schwere und eine Trägheit. Materie erzeugt ein Gravitationsfeld und reagiert darauf. Durch ihre Trägheit können sie bei Kollisionen Impuls aufnehmen und abgeben.

Kometen

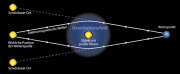
Kometen sind am Himmel an ihrem hellen Schweif zu erkennen, der immer von der Sonne weg zeigt. Sie sind aus der Nähe betrachtet ein einige Kilometer große "schmutzige Schneebälle" aus Gestein, Staub und Eis. Kometen haben eine stark elliptische Umlaufbahn um die Sonne oder sogar eine aperiodische Bahn, dann kommen sie der Sonne nur einmal nahe. Durch die Nähe zur Sonne steigt die Temperatur auf dem Kometen und es bilden sich Gase. Das Licht von der Sonne und der Teilchenstrom der Sonne drücken die ausgestoßenen Gase und Staub des Kometen von der Sonne weg.

Einsteinringe durch Lichtablenkung

Große Massen wie Sterne oder schwarze Löcher können das Licht durch ihr Gravitationsfeld merklich ablenken[2]. Bei Sonnenfinsternissen kann man deswegen am Rand der Sonne Sterne sehen, die eigentlich von der Sonne verdeckt wären. Bei der Beobachtung von Sternen und Galaxien hinter einer großen Masse kommt es zum Gravitationslinsen-Effekt[3].


Versuch: Compton-Streuung

Versuchsaufbau

Bei einem Streuversuch spielt man, vereinfacht gesagt, Billiard. Man läßt zum Beispiel Licht oder andere Teilchen auf einen Streukörper fallen und schaut sich an, wie die Photonen aus dem "target" wieder herauskommen. Daraus kann man Rückschlüsse sowohl über das Licht, als auch über das Target ziehen.

In diesem Fall wird Gamma-Strahlung einer Röntgenröhre auf einen Aluminiumkörper geschickt. Dann misst man unter verschiedenen Winkeln die getreute Strahlung. Und zwar mit Hilfe eines Szintillationszählers, der die Energie und die Anzahl der Photonen messen kann.

Beobachtung

Je größer der Winkel ist, unter dem man die gestreute Strahlung untersucht, desto geringer ist die Energie der Photonen.

Erklärung

Nach dem Wellenmodell ist es überraschend und nicht erklärbar, dass die Wellenlänge der gestreuten Strahlung sich verändert. Denn die elektromagnetischen Wellen regen den Streukörper zu Schwingungen in der eigenen Frequenz an und der Streukörper wiederum sendet Wellen dieser Frequenz aus.

Zur Erklärung verwendet man das Teilchenmodell des Lichts. Die Lichtteilchen treffen auf den Streukörper und stoßen mit ihm zusammen. Ähnlich wie Billiardkugeln geben sie durch den Stoß ein Teil ihrer Energie ab und ändern ihren Impuls in Stärke und Richtung. Die größere Wellenlänge der gestreuten Photonen liegt also an der geringeren Energie der Photonen, denn Photonen mit geringerer Energie haben eine geringere Frequenz, bzw. eine größere Wellenlänge.

Neu ist, dass man einem Photon außer einer Energiemenge auch eine Masse und einen Impuls zuweist, die mit der Wellenlänge zusammenhängen.

Dadurch ist man in der seltsamen Lage elektromagnetischen Wellen, die aus E- und H-Feldern bestehen, eine Masse zuzuordnen. Grundlage dazu ist die berühmte Energie-Masse-Äquivalenz von Albert Einsteins spezieller Relativitätstheorie:

[math]E=m\,c^2=h\,f[/math]

Photonen haben also ausschließlich wegen ihres Energiegehalts eine Masse:

[math]m=\frac{h\,f}{c^2}=\frac{h\,f}{c\,\lambda\,f}=\frac{h}{c\,\lambda}[/math]

Weil sich Photonen mit Lichtgeschwindigkeit ausbreiten (zumindest im Vakuum) haben sie den Impuls:

[math]p=m\,c=\frac{h\,f}{c}=\frac{h}{\lambda}[/math]

Diese Formel ist mathematisch schön einfach. Inhaltlich ist sie allerdings völlig unverständlich. Einerseits enthält sie mit dem Impuls den Gedanken der Teilchentheorie, andererseits mit der Wellenlänge die Wellentheorie!

Für Röntgenlicht der Wellenlänge [math]10^{-10}\rm m[/math] ergibt sich z.B. daraus: [math]m=2{,}2\cdot10^{-32}\rm{kg}[/math] und [math]p=6{,}6\cdot10^{-24}\rm\, kg\,\frac{m}{s}[/math]

Zum Vergleich: Ein Elektron hat eine Masse von [math]m=91\cdot10^{-32}\rm{kg}[/math], also etwa fünfmal so viel. Um den gleichen Impuls wie das Röntgenphoton zu bekommen, müsste man das Elektron mit einer Spannung von ca. 150 Volt beschleunigen.

Die Photonen einer elektromagnetische Welle besitzen eine (schwere und träge) Masse.
Sie enthalten Energie und Impuls:

[math]E = m\,c^2 = h\,f \qquad p=m\, c = \frac{h}{\lambda}[/math]

Die Röntgenphotonen treffen also auf das Target und werden wie Billiardkugeln getreut. Fragt sich womit sie zusammenstoßen. Compton hatte die Idee, dass die Photonen mit den schwach gebundenen Elektronen zusammenstoßen, die Graphit oder Aluminium auch elektrisch leitfähig macht. Um diese Elektronen von den Atomkernen zu trennen ist wenig Energie nötig, weshalb der Streuvorgang davon nur wenig beeinflusst wird.

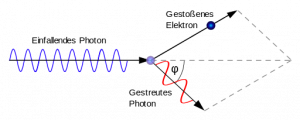
Den Zusammenstoß von Photon und Graphitelektron kann man sich vereinfacht als den Zusammenstoß zweier Kugeln vorstellen. Bei dem elastischen Stoß bleibt die kinetische Energie erhalten, es gibt keine "Reibung". Außerdem nimmt man an, daß das Elektron vor dem Zusammenstoß ruht. Durch die Erhaltung von Energie und Impuls ist der Stoßvorgang vollständig beschrieben.

Durch den Stoß verändert sich der Impuls des Photons in Richtung und Betrag. Je größer der Ablenkungswinkel ist, desto mehr nimmt der Impulsbetrag des gestreuten Photons ab. Das kann man gut durch die Vektoraddition der Impulse sehen. Diese Animation gestattet es, für unterschiedliche Massen den Stoß zweier Scheiben zu simulieren.

Bei dieser Animation (draufklicken!) wird das einfache Bohrsche Atommodell zugrunde gelegt. Seltsamerweise werden die Elektronen als kleine rote Kugeln dargestellt, das Photon aber nur als Pfeil.
Diese Zeichnung zeigt, wie die Bahn des Photons sich durch den Stoß um den Winkel [math]\varphi[/math] verändert. Seltsamerweise ist das Photon mit einer Sinuskurve eher wie eine Welle dargestellt, das Elektron aber als kleine Kugel.
Animation der Impulserhaltung beim Compton-Effekt

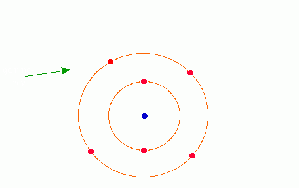
Bei dieser Animation wird die Impulsänderung beim Stoß veranschaulicht. Das Elektron ruht vor dem Zusammenstoß.

Man kann die Masse des Photons als Anteil der Elektronenmasse einstellen. Zu Beginn beträgt sie 5% der Elektronenmasse. Dabei ändert sich natürlich auch der Impuls des Photons. Aus Darstellungsgründen bleibt der Impuls des einfallenden Photons aber immer gleich!

Mit dem grünen Schieberegler kann man den Auftreffpunkt des Photons auf das Elektron verschieben.

(Zur Datei und zum Programm)

Links

Fußnoten

  1. ↑ Paranoid on the English Wikipedia (CC3.0)
  2. ↑ Siehe: Lichtablenkung durch Gravitation (Max Planck-Institut für Gravitationsphysik)
  3. ↑ Siehe: Wikipedia: Gravitationslinseneffekt
Von „http://schulphysikwiki.de/index.php?title=Masse_%26_Impuls_von_Photonen_-_Der_Compton-Effekt&oldid=16928“