Aufgaben zum Elektro-Magnetismus (Lösungen): Unterschied zwischen den Versionen
(→Ein fallender Magnet) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Elektro-Magnetismus|'''Elektro-Magnetismus''']]) | |
| + | *[[Aufgaben zum Elektro-Magnetismus|'''Zurück zu den Aufgaben''']] | ||
| + | |||
| + | ==Grundlagen== | ||
===Verschiedene Wege zur Induktionsspannung=== | ===Verschiedene Wege zur Induktionsspannung=== | ||
Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese. | Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese. | ||
Version vom 14. Mai 2017, 15:37 Uhr
(Kursstufe > Elektro-Magnetismus)
Inhaltsverzeichnis
Grundlagen
Verschiedene Wege zur Induktionsspannung
Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese.
- Eine Leiterschleife in ein Magnetfeld eintauchen (herausziehen).
- Durch das Eintauchen vergrößert (verringert) sich die "Anzahl der Feldlinien" durch die Schleife, genauer nimmt der magnetische Fluss durch die Schleife zu (ab). Es wird eine Spannung an der Schleife erzeugt (andere Polung).
- Eine Leiterschleife in einem Magnetfeld vergrößern (verkleinern). Auch hier darf die Schleife dabei nicht parallel zu den Feldlinien sein.
- Wiederum nimmt der magnetische Fluss durch die Schleife zu (ab).
- Der Nordpol eines Festmagneten wird der Schleife genähert.
- Die Feldstärke ist in der Nähe des Pols größer, deshalb nimmt der magnetische Fluß durch die Schleife zu.
- Die Schleife befindet sich im Magnetfeld einer Spule. Der Strom durch die Spule steigt an (nimmt ab).
- Durch die Zunahme des Stromes steigt auch die Feldstärke innerhalb der Spule an und somit der magnetische Fluß durch die Schleife. (Bei abnehmender Stromstärke sinkt der Fluß und die Polung der Spannung ist umgekehrt.)
- Die Schleife befindet sich um einen Eisenkern. Der Pol eines Festmagneten wird dem Eisenkern genähert.
- Durch die Annäherung des Magneten vergrößert sich die Magnetisierung des Eisens und der magnetische Fluss durch die Schleife nimmt zu.
- Die Schleife und eine Spule befinden sich um einen Eisenkern, sie sind "induktiv gekoppelt". Durch die Spule fließt ein Strom mit zunehmender Stromstärke.
- Der Spulenstrom führt zu einer Magnetisierung des Eisenkerns. Da die Stromstärke zunimmt, steigt auch die Magnetisierung mit der Zeit an. Dadurch steigt der magnetische Fluss durch die Schleife an und eine Spannung wird erzeugt.
- Eine Schleife wird in einem Magnetfeld gedreht. Die Drehachse ist nicht parallel zu den Feldlinien.
- Je nach Lage der Schleife "gehen viele oder wenige Feldlinien durch die Schleife", der magnetische Fluß ist groß oder klein. Ist die Schleife parallel zu den Feldlinien, so verschwindet der Fluß durch die Schleife. Die Drehung führt daher zu einer Änderung des magnetischen Flußes durch die Schleife und somit zu einer Induktionsspannung.
Magnetischer Fluss
Erläutern Sie anhand von verschiedenen Beispielen, was der magnetische Fluss durch eine Fläche ist.
- Hält man den Pol eines Festmagneten nahe vor eine Leiterschleife, so ist der magnetische Fluß durch die von der Schleife umrandete Fläche groß, weil "viele Magnetfeldlinien" durch die Fläche gehen. Genauer ist das Produkt von mittlerer Feldstärke und Fläche groß.
- Hält man den Festmagneten so an die Schleife, dass die Feldlinien parallel zur Schleife sind, so verlaufen gar keine Feldlinien durch die Fläche und der magnetische Fluß verschwindet. In diesem Fall ist das Produkt von Feldstärke und Fläche Null, weil die effektive Fläche senkrecht zu den Feldlinien Null ist.
- Befindet sich ein magnetisierter Eisenkern in einer Leiterschleife, so gibt es einen magnetischen Fluß durch die Fläche der Schleife, weil "viele Magnetisierungslinien" durch die Fläche gehen. Genauer ist der magnetische Fluß das Produkt aus mittlerer Magnetisierung und Fläche.
Induktionsgesetz
- Wie lautet das Induktionsgesetz in Worten?
- Die Induktionsspannung an einer Leiterschleife ist die zeitliche Änderung des magnetischen Flusses.
- Wie lautet das Induktionsgesetz als Formel in den folgenden Situationen:
- Die Formeln gelten für eine Induktionsspule mit n Windungen.
- Der magnetische Fluss ist:
- [math]\Phi = \mu_0 \, H \, A + \mu_0 \, M \, A = \mu_0 \mu_r \, H \, A [/math]
- Allgemeingültig
- [math]U_i = n \, \dot \Phi[/math]
- Ohne Magnetisierung, nur die Feldstärke ändert sich, die Schleifenfläche ist konstant.
- [math]U_i = n \, \mu_0 \, \dot H \, A \approx n \, \frac{\Delta H}{\Delta t}\, A[/math]
- Ohne Magnetisierung, nur die Schleifenfläche ändert sich, die Feldstärke ist konstant.
- [math]U_i = n \, \mu_0 \, H \, \dot A \approx n \,\mu_0 \, H \, \frac{\Delta A}{\Delta t}[/math]
- Ohne Feld, nur die Magnetisierung ändert sich, die Schleifenfläche ist konstant.
- [math]U_i = n \, \mu_0 \, \dot M \, A \approx n \, \frac{\Delta M}{\Delta t} \, A[/math]
Anwendung des Induktionsgesetzes
Primär und Sekundärspule
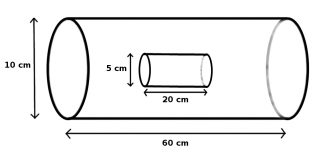
Innerhalb einer "großen" Primärspule mit 500 Windungen liegt eine "kleine" Sekundärspule mit 2000 Windungen. (Siehe Zeichnung) Durch die Primärspule fließt ein Strom von zwei Ampère.
Die Spule wird dann von der Spannungsquelle getrennt, wodurch die Stromstärke innerhalb von einer tausendstel Sekunde auf Null Ampère zurückgeht.
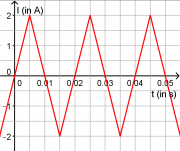
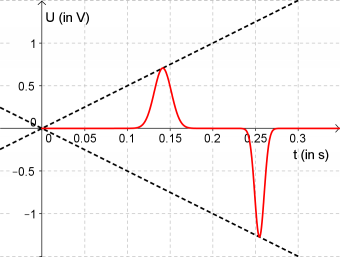
Danach legt man an die Primärspule eine Dreiecksspannung mit einer Frequenz von 50Hz an, die zu einer maximalen Stromstärke von 2A führt. (Siehe Zeichnung) Zur Messung der Spannung an der Sekundärspule wird ein Oszilloskop angeschlossen.
a) Wie groß ist zu Beginn die magnetische Feldstärke? Berechnen Sie den magnetischen Fluss durch die Primär- und die Sekundärspule.
- Die Spule betrachtet man als "schlanke Spule" und berechnet dann nach der Definition der magnetischen Feldstärke:
- [math]H=\frac{n_1\, I}{l}= \rm \frac{500\cdot 2\,A}{0{,}6\,m}= \rm 1667\, \frac{A}{m}[/math]
- Die Luft ist nicht magnetisierbar, deswegen ist die Flussdichte einfach das Produkt der Feldstärke mit der Feldkonstante:
- [math]B=\mu_0\,H = 1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \cdot 1667\, \rm \frac{A}{m}= 0{,}002095\,\rm\frac{Vs}{m^2} \quad (= 2{,}095\cdot 10^{-3}\,\frac{Wb}{m^2}= 2{,}095 \,mT)[/math]
- Die Fläche der Spulen berechnen sich mit Hilfe des Radius:
- [math]A_1=\pi\, r_1^2 = \pi\cdot (0{,}05\,\rm m)^2 = 0{,}007854\,\rm m^2 \quad (= 78{,}54\,\rm cm^2)[/math]
- [math]A_2=\pi\, r_2^2 = \pi\cdot (0{,}025\,\rm m)^2 = 0{,}001969\,\rm m^2 \quad (= 19{,}69\,\rm cm^2)[/math]
- Aus der Flussdichte und der Fläche kann man nun den magnetischen Fluss berechnen:
- [math]\Phi_1 = B\, A_1 = 2{,}095\cdot 10^{-3}\,\rm\frac{Wb}{m^2} \cdot 0{,}007854\,\rm m^2 = 1{,}645\cdot 10^{-5}\,\rm Wb \quad (V s\,\text{oder}\,T m^2)[/math]
- [math]\Phi_2 = B\, A_2 = 2{,}095\cdot 10^{-3}\,\rm\frac{Wb}{m^2} \cdot 0{,}001969\,\rm m^2 = 4{,}114\cdot 10^{-6}\,\rm Wb [/math]
b) Während des Trennens von der Spannungsquelle registriert die Sekundärspule eine Spannung. Begründen Sie dies und berechnen Sie die Spannung.
- Durch die fehlende Spannung sinkt die Stromstärke auf Null ab. Währenddessen ändert sich die Feldstärke und damit auch der magnetische Fluss in der Sekundärspule.
- Zur Berechnung der Induktionsspannung verwendet man das Induktionsgesetz:
- [math]U_i = n_2\,\dot \Phi = n_2\,\frac{\Delta \Phi}{\Delta t} =2000\cdot \frac{4{,}114\cdot 10^{-6}\,\rm Wb}{10^{-3}\,\rm s} = 8{,}23\,\rm V \qquad \left(\rm\frac{Wb}{s} = \rm\frac{V s}{s} \right)[/math]
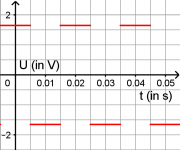
c) Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der mit dem Oszilloskop gemessenen Induktionsspannung ein.
- Wieder wird durch die Änderung der Stromstärke der magnetische Fluss geändert.Im Induktionsgesetz kann man sich nun aussuchen, welche Änderungsrate man ausrechnet. Man kann die Änderung der Flussdichte, der Feldstärke oder der Stromstärke verwenden:
- [math]U_i = n_2\,\dot \Phi = n_2 \,\dot B\, A = n_2 \,\mu_0 \dot H \, A = n_2 \,\mu_0 \frac{n_1}{l} \dot I \, A \qquad \left(= \mu_0 \, \frac{A\, n_1\, n_2}{l} \cdot \dot I \right)[/math][1]
- Weil hier die Stromstärke sich konstant ändert, kann man die Änderungsraten als Differenzenquotient berechnen:
- [math]U_i = n_2 \,\frac{\Delta \Phi}{\Delta t} = n_2 \,\frac{\Delta B}{\Delta t}\, A = n_2 \,\mu_0\frac{\Delta H}{\Delta t}\, A = n_2 \,\mu_0 \frac{n_1}{l}\frac{\Delta I}{\Delta t}\, A[/math]
- Die Stromstärke fällt oder oder steigt innerhalb von [math]0{,}01\,\rm s[/math] um [math]4\,\rm A[/math]:
- [math]\frac{\Delta I}{\Delta t} = \rm \frac{4\,A}{0{,}01\,\rm s} = 400\,\rm\frac{A}{s}[/math]
- Bei ansteigender Stromstärke beträgt die Induktionsspannung daher:
- [math]U_i = n_2\,\mu_0 \frac{n_1}{l}\frac{\Delta I}{\Delta t}\, A = 2000\cdot 1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \cdot \frac{500}{0{,}6\,\rm m}\cdot \frac{4\,\rm A}{0{,}01\,\rm s}\, 0{,}001969\,\rm m^2 = 0{,}165\,\rm V \quad (= 165\,\rm mV)[/math]
- Jetzt kann man den Verlauf der Induktionsspannung zeichnen.
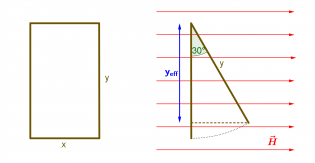
- Wie ändert sich der Verlauf der Induktionsspannung, wenn die Sekundärspule in einem Winkel von 30° in der Primärspule liegt?
- Nun ist die von der Flussdichte durchsetzte effektive Schleifenfläche kleiner, also sinkt auch die Induktionsspannung, die proportional zur Fläche ist.
- Die Abnahme läßt sich auch berechnen. Der Einfachheit halber nimmt man zunächst eine Schleife mit rechteckiger Fläche. Durch die 30°-Drehung verkürzt sich die effektive Breite x der Rechteckschleife:
- [math]\cos(30^\circ)=\frac{x_{eff}}{x}\quad \Rightarrow \quad x_{eff}= \cos(30^\circ) \, x = \frac{\sqrt 3}{2} \, x \approx \, 0{,}87 \cdot x[/math]
- Die Länge y des Rechtecks bleibt unverändert, daher verkleinert sich die Fläche auf 87%:
- [math] A_{eff} \approx \, 0{,}87 \cdot A[/math]
- Dementsprechend geht auch die Induktionsspannung auf 87% zurück und beträgt nur noch:
- [math]U_i=0{,}87 \cdot 165\,\rm mV = 144\,\rm mV[/math]
Die Überlegung stimmt auch noch für eine beliebige krummlinig begrenzte Fläche. In diesem Fall kann man die Fläche durch kleine Rechtecke ausfüllen, was bis auf kleinere Lücken geht. Für die Rechtecke gilt die obere Betrachtung schon. Verwendet man nun immer kleinere Rechtecke, so werden die Lücken und somit der Fehler immer kleiner. Das Vorgehen ist nichts anderes als die Berechnung der Fläche mit einem Integral.
Eine Spule taucht ein
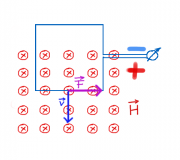
Eine Spule wird innerhalb von 2 Sekunden in ein homogenes Magnetfeld mit einer Feldstärke von 1000A/m senkrecht zu den Feldlinien eingetaucht. Die Spule hat einen quadratischen Querschnitt von 5cm Kantenlänge und 300 Windungen. Sie ist an ein Spannungsmessgerät angeschlossen.
a) Berechnen Sie die gemessene Induktionsspannung.
- Die Induktionsspannung berechnet sich aus der Änderung des magnetischen Flusses. Vor dem Eintauchen in das Feld ist die wirksame Fläche der Schleife noch Null und es gibt keinen Fluss durch die Schleife. Während des Eintauchens gehen wir davon aus, dass die Fläche gleichmäßig bis auf die gesamte Schleifenfläche ansteigt.
- [math]U_i = n\,\dot \Phi = n\, \frac{\Delta \Phi}{\Delta t}[/math]
- Den magnetischen Fluss berechnet man aus Feldstärke und Fläche:
- [math] \begin{array}{rcl} U_i &=& n\,\frac{\mu_0\, H\, \Delta A}{\Delta t} \\ &=& 300\cdot \frac{1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \, 1000 {\rm \frac{A}{m}} \, (0{,}05\,\rm m)^2}{2\,\rm s}\\ &=& 300\cdot \frac{3{,}14\cdot 10^{-6} \,\rm Vs}{2\,\rm s}\\ &=& 300\cdot 1{,}57\cdot 10^{-6} \,\rm V\\ &=& 4{,}71\cdot 10^{-4} \,\rm V\\ &=& 0{,}471\,\rm mV\\ \end{array} [/math]
b) Was kann man messen, wenn die Spule innerhalb des Feldes bewegt wird?
- Befindet sich die Spule vollständig im Magnetfeld, so ändert sich der magnetische Fluss durch die Schleife nicht mehr. Deshalb wird auch keine Spannung induziert.
c) Kennzeichnen Sie die Polung der Induktionsspannung mit + und - in der Zeichnung.
- Mit Hilfe der UVW-Regel / Drei-Finger-Regel erhält man die Kraftwirkung auf die Ladungen im Kabel der Schleife. Die positive Ladung wird also nach rechts gedrückt und deshalb entsteht auf dieser Seite des Spannungsmessgerätes auch ein positiver Ladungsüberschuß. (Betrachtet man die Elektronen im Kabel, verwendet man die linke Hand. Die Elektronen werden nach links gedrückt und man erhält das gleiche Ergebnis.)
Magnet im freien Fall
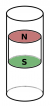
Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein Oszilloskop angeschlossen.
- Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung qualitativ in ein Koordinatensystem und erläutern Sie ihr Ergebnis.
|
Nach dem Induktionsgesetz wird eine Spannung induziert, wenn sich der magnetische Fluss [math]\Phi = B \cdot A[/math] durch die Spule ändert.
|
Der magnetische Fluss entspricht in der animierten Zeichnung der Anzahl der Flussdichtelinien durch die Spule. Am blauen Punkt läßt sich der Magnet verschieben.
|
Energieübertragung
Transformator
- a) Warum kann man einen Transformator nicht mit Gleichstrom, sondern nur mit Wechselstrom betreiben?
- Der Transformator arbeitet mit Induktionsspannung. Eine Induktionsspannung gibt es aber nur, wenn sich innerhalb einer Spule der magnetische Fluß verändert. Bei Gleichstrom hätte man aber keine Veränderung, sondern, wie der Name schon sagt, ein zeitlich konstanten magnetischen Fluß.
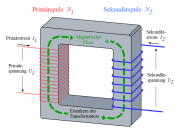
- b) Erläutern Sie anhand der Zeichnung die Funktionsweise eines Trafos.
-
- Der Trafo besteht aus zwei Spulen, die um einen gemeinsamen Eisenkern gewickelt sind. An eine davon, der sogenannten "Primärspule", legt man eine Wechselspannung an.
- Der durch die Primärspule fließende Strom verursacht ein Magnetfeld im Inneren der Spule, wodurch die Elementarmagnete des Eisen ausgerichtet werden: Der Eisenkern wird magnetisiert.
- Weil Stärke und Richtung des Stroms sich ständig ändern, ändern sich auch die Stärke und Richtung der Magnetisierung ständig. Das heißt, der magnetische Fluß durch den Eisenkern ändert sich ständig! Das wiederum ruft eine Induktionsspannung bei der zweiten Spule, der sogenannten "Sekundärspule" hervor, die auch eine Wechselspannung ist.
- Die Größe der Induktionsspannung ist abhängig von der Windungszahl der Sekundärspule. Haben Primär- und Sekundärspule die gleiche Anzahl von Windungen, so erhält man als Sekundärspannung, bis auf auftetende Verluste, die Primärspannung. Will man eine größere Spannung haben, verwendet man mehr Windungen, will man eine kleinere Spannung haben, verwendet man weniger Windungen.
- In der Zeichnung hat die Primärspule ca. 15 Windungen und die Sekundärspule ca. 6 Windungen. Die Sekundärspannung beträgt daher ungefähr die Hälfte der Pimärspannung, genauer: [math]U_2=\frac{6}{15}\, U_1 = 0{,}4 \, U_2[/math].
- c) Wie könnte der Trafo eines Netzgerätes gebaut sein, der ein Handy mit 5,7V Spannung versorgt?
- An der Steckdose liegt eine Wechselspannung mit der effektiven Spannung von 230V an. Der Trafo muß also weniger Sekundärwindungen als Primärwindungen haben, damit die Sekundärspannung kleiner ist als 230V. Das Verhältnis der Spannungen beträgt: [math] \frac{230\,\rm V}{5{,}7\,\rm V}\approx 40 [/math].
- Also muss die Primärspule 40 mal mehr Windungen haben, als die Sekundärspule, zum Beispiel 4000 Windungen, und die Sekundärspule nur 100 Windungen.
- Wer lieber mit Formeln rechnet, kann auch mit der Verhältnisgleichung arbeiten:
- [math] \begin{array}{rrcll} & \frac{U_1}{U_2} &= & \frac{n_1}{n_2} \\ & \frac{230\,\rm V}{5{,}7\,\rm V} &= & \frac{n_1}{n_2} \\ \Rightarrow & 40 &\approx& \frac{n_1}{n_2} & | \cdot n_2 \\ \Rightarrow & 40 \, n_2 &\approx& n_1 & \\ \end{array} [/math]
Ein schwingender Magnet
Der Nordpol eines Stabmagneten schwingt innerhalb einer Spule auf und ab. Sobald man die Spule mit einem Kabel kurzschließt, wird der Magnet gebremst und bleibt schließlich stehen.
- a) Erklären Sie diese Beobachtung.
- Am einfachsten ist es, den Weg der Energie zu verfolgen:
- Zu Beginn steckt man durch Hochheben oder Anschubsen Energie in die Schwingung. Danach wechselt die nur ihre Form (ihren Träger), bleibt aber in der Summe in etwa konstant, was man an der konstanten Amplitude der Schwingung sehen kann.
- Durch die Bewegung des Magneten wird zwar in der Spule eine Spannung induziert, aber kaum Energie übertragen.
- Erst mit dem Kurzschließen der Spule fließt die Energie aus der Schwingung heraus, die Schwingung wird abgebremst. Denn nun kann in der Spule Strom fließen, dass heißt, die Schwingung treibt mit ihrer Energie den Stromfluß an. Weil die Kupferdrähte der Spule dem Strom einen Widerstand entgegensetzen, werden die Drähte warm. Die Energie der Schwingung steckt am Ende des Vorgangs also in der Wärmeenergie des Kupferdrahtes, bzw. wird auf die im Draht erzeugte Entropie umgeladen.
- b) Was würde passieren, wenn man den Versuch mit einer supraleitenden Spule durchführen würde?
- Eine supraleitende Spule hat keinen ohmschen Widerstand, der elektrische Strom fließt ohne dass die Spule sich erwärmt. Das System aus schwingendem Magneten und Spule ist fast abgeschlossen, es verliert nur ein bischen Energie durch die Luftreibung und die innere Reibung der Feder.
- Fließt Strom durch die Spule, so baut sich ein Magnetfeld auf, in dem Energie gespeichert wird. Diese Energie wird der Schwingung entzogen, wenn der Magnet sich auf die Spule zu bewegt. Dann vergrößert sich der magnetische Fluß, eine Spannung wird induziert und der Strom angetrieben. Entfernt sich der Magnet von der Spule, so wird das Magnetfeld abgebaut und die Feldenergie fließt wieder in die Bewegung zurück. Der Magnet wird also bei der Bewegung auf die Spule zu abgebremst und bei der Bewegung von der Spule weg beschleunigt.
- Dadurch schwingt der Magnet mit einer höheren Frequenz als ohne die Spule.
- Dieser Effekt tritt auch bei der "normalen" Spule nicht auf, denn die beschleunigende Wirkung entfällt hier.
- Will man das Geschehen quantitativ fassen, so kann man die Energie der Spule mit dem magnetischen Fluß durch die Spule berechnen:
- [math]W = \frac{1}{2}\,L\,I^2 = \frac{1}{2}\,n\Phi\,I = \frac{(n\,\Phi)^2}{2\,L} [/math]
- Zu jeder Position des Magneten gehört ein bestimmter magnetischer Fluß, aus dem man die Energiemenge der Spule berechnen kann. Die räumliche Änderung der magnetischen Energie gibt die Kraftwirkung auf den Magneten an.
Ein fallender Magnet
Ein Magnet fällt durch ein Kupferrohr
- a) Was kann man beobachten?
- Der Magnet fällt langsam, mit einer konstanten Geschwindigkeit durch das Rohr.
- b) Wieso kann man für den Versuch kein Plastikrohr und auch kein Eisenrohr verwenden?
- In einem Plastikrohr können keine Ströme induziert werden, der Effekt bleibt aus. Das wird hier ausführlich erläutert.
- Das Eisenrohr dagegen kann magnetisiert werden und der Magnet fällt gar nicht, sondern bleibt am Rohr hängen.
- c) Wie verändert sich das Versuchsergebnis, wenn man ein Kupferrohr mit dickeren Wänden benutzt?
- Bei einer bestimmten Geschwindigkeit wird immer die gleiche Spannung induziert, unabhängig von der Dicke des Rohres. Aber je dicker die Wand, desto geringer ist der elektrische Widerstand. Deshalb fließt bei der gleichen Geschwindigkeit mehr Energie pro Zeit aus der Bewegung, der Magnet wird stärker gebremst:
- [math]P = U\, I = \frac{U^2}{R}[/math]
- [math]P = F_{mag}\,v[/math]
- Das Gleichgewicht aus Gewichtskraft und magnetischer Kraft stellt sich daher bei einer geringeren Geschwindigkeit ein.
- d) Wie könnte man es erreichen, dass der Magnet schwebt?
- Dazu muß der elektrische Widerstand vollständig verschwinden, was man bei einem Supraleiter tatsächlich auch erreichen kann! (Siehe diese Demonstration der Harvard-University)
Induktionskochplatte
- Erklären Sie in Text und Bild, wie eine Induktionskochplatte funktioniert.
- Was man bei einem Transformator vermeiden möchte ist hier das Wirkungsprinzip.
- Zur Erklärung nehmen wir vereinfachend an, dass sich nur eine große Spule unter dem Topf befindet. Die Spule ist an eine hochfrequente Wechselspannung angeschlossen, wodurch der Topfboden von einem sich ständig ändernden Magnetfeld durchsetzt wird. Deshalb fließt im Boden um das Magnetfeld ein Kreisstrom, der, wegen des ohmschen Widerstandes des Bodens, den Boden erhitzt.
- Ein zweiter Erwärmungseffekt stellt sich dadurch ein, dass der Topfboden ständig ummagnetisiert wird. Dies geschieht nicht verlustfrei, sondern führt auch zu einer Erwärmung des Bodens.
- Induktionsherde haben in der Regel eine hitzebeständige Glasplatte als Topfauflage. Warum erhitzt der Herd nur den Topf und nicht das darin befindliche Essen oder die Glasplatte? (Warum wird die Glasplatte beim Kochen trotzdem heiß?)
- Sowohl Glas als auch das Essen können den elektrischen Strom nicht leiten und sind nicht magnetisierbar. Sie werden aber, hauptsächlich durch Wärmeleitung, indirekt vom heißen Topfboden erwärmt.
Wirbelstrombremse
- Nennen Sie Beispiele, bei denen eine Wirbelstrombremse eingesetzt wird.
- Erläutern Sie das Funktionsprinzip mit einer Zeichnung.
- Erklären Sie dabei mit Hilfe des Induktionsgesetzes, wie die Ströme fließen.
- Wie kann man die Bremswirkung mit der Energieerhaltung begründen?
Selbstinduktion
- a) Erklären Sie den Begriff der Selbstinduktion indem Sie einen passenden Versuch beschreiben.
- b) Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist.
Induktivität
- a) Eine Spule hat eine Induktivität von 10 H (Henry).
- Was bedeutet das?
- b) Eine Spule hat 1000 Windungen und einen geschlossenen Eisenkern mit einer Permeabilitätszahl von [math]\mu_r = 2000[/math].
- Berechnen Sie ihre Induktivität.
Elektrische Wirbelfelder
Fußnoten
- ↑ Diese Formel zur Berechnung der Spannung an einer Spule in Abhängigkeit von der Stromstärkeänderung spielt bei der Induktivität einer Spule eine Rolle.