Aufgaben zu elektromagnetischen Schwingungen und Wellen (Lösungen): Unterschied zwischen den Versionen
Aus Schulphysikwiki
(→Qual der Wahl) |
(→Gummibärchen in der Mikrowelle) |
||
| (9 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
===Vergleich von elektrischer und mechanischer Schwingung=== | ===Vergleich von elektrischer und mechanischer Schwingung=== | ||
Vergleichen Sie einen elektrischen Schwingkreis mit einem horizontalen Federpendel mit Zeichnungen, einem erklärenden Text und einer Gegenüberstellung sich entsprechender Größen. | Vergleichen Sie einen elektrischen Schwingkreis mit einem horizontalen Federpendel mit Zeichnungen, einem erklärenden Text und einer Gegenüberstellung sich entsprechender Größen. | ||
| + | :Der Vergleich ist auf [[Der_elektrische_Schwingkreis#Vergleich_mit_mechanischen_Schwingungen|dieser Seite]] schön zu sehen. | ||
===Ein Schwingkreis=== | ===Ein Schwingkreis=== | ||
| Zeile 36: | Zeile 37: | ||
=====Feldlinienbild===== | =====Feldlinienbild===== | ||
*Zeichen Sie das Feldlinienbild einer ebenen elektro-magnetischen Welle. | *Zeichen Sie das Feldlinienbild einer ebenen elektro-magnetischen Welle. | ||
| + | :Das sieht man sich am besten in dieser [[Grundbegriffe_und_Beispiele_zu_elektromagnetischen_Wellen#Animation_einer_ebenen_elektro-magnetischen_Welle|Animation]] an. | ||
| + | :Die Feldlinien des Magnetfeldes und des elektrischen Feldes stehen immer aufeinander und zur Ausbreitungsrichtung senkrecht. | ||
=====Wellenlänge und Frequenz===== | =====Wellenlänge und Frequenz===== | ||
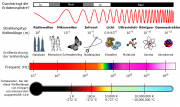
| + | [[Datei:Elektromagnetisches Spektrum - Eigenschaften.png|thumb|Dieses Bild sagt alles:)]] | ||
*Elektromagnetische Wellen haben, je nach Wellenlänge, unterschiedliche Namen bekommen. Nennen Sie verschiedene und sortieren Sie diese von langen zu kurzen Wellenlängen. | *Elektromagnetische Wellen haben, je nach Wellenlänge, unterschiedliche Namen bekommen. Nennen Sie verschiedene und sortieren Sie diese von langen zu kurzen Wellenlängen. | ||
*Berechnen Sie die Wellenlänge bei einem Radar, dass mit einer Frequenz von 5 GHz arbeitet. | *Berechnen Sie die Wellenlänge bei einem Radar, dass mit einer Frequenz von 5 GHz arbeitet. | ||
| + | :Wie bei allen Wellen gibt es einen festen Zusammenhang zwischen Ausbreitungsgeschwindigkeit, (hier der Lichtgeschwindigkeit c=300.000km/s), der Wellenlänge und der Frequenz: <math>c = \lambda \, f </math>. | ||
| + | :Also folgt für die Wellenlänge: | ||
| + | ::<math>\lambda = \frac{c}{f} = \frac{3\cdot 10^{8}\,\rm \frac{m}{s}}{5\cdot 10^{9}\,\rm Hz} = 0{,}06\,\rm m = 6\,\rm cm </math> | ||
*Berechnen Sie die Frequenz einer "roten Lichtwelle" mit einer Wellenlänge von 630 nm. | *Berechnen Sie die Frequenz einer "roten Lichtwelle" mit einer Wellenlänge von 630 nm. | ||
| + | :Diesmal löst man nach der Frequenz auf: | ||
| + | ::<math> f = \frac{c}{\lambda} = \frac{3\cdot 10^{8}\,\rm \frac{m}{s}}{630\cdot 10^{-9}\,\rm m} = 4{,}76\cdot 10^{14}\,\rm Hz = 476\,\rm T Hz</math> | ||
=====Mikrowellenherd===== | =====Mikrowellenherd===== | ||
*Warum kann man in der Mikrowelle schlecht ein Brot erwärmen, aber sehr gut eine Suppe erhitzen? | *Warum kann man in der Mikrowelle schlecht ein Brot erwärmen, aber sehr gut eine Suppe erhitzen? | ||
| + | :In Brot befindet sich, im Gegensatz zur Suppe, nur wenig Wasser. Eine Mikrowelle ist aber besonders darauf ausgelegt Wasser zu erhitzen. Die Wassermoleküle haben nämlich einen elektrischen Dipol und werden von dem elektrischen Wechselfeld ständig gedreht, wodurch sich die "innere Energie" der Speisen, also die Wärmeenergie erhöht. | ||
*Warum haben Mikrowellen in der Regel einen Drehteller? | *Warum haben Mikrowellen in der Regel einen Drehteller? | ||
| + | :Durch Reflektionen der Wellen an den Metallwänden und die Überlagerung mit den noch nicht reflektierten Wellen entsteht im Innenraum eine stehende, elektromagnetische Welle mit Knoten und Bäuchen. An den Bäuchen befindet sich ein besonders starkes Wechselfeld, bei den Knoten ein sehr schwaches. Ohne Drehteller würden die Speisen ungleichmäßig gewärmt. | ||
=====Gummibärchen in der Mikrowelle===== | =====Gummibärchen in der Mikrowelle===== | ||
[[Datei:Mikrowelle_Gummibärchen_1.jpg|thumb]] | [[Datei:Mikrowelle_Gummibärchen_1.jpg|thumb]] | ||
*Erklären Sie das Zustandekommen der Unregelmäßigkeiten bei den geschmolzenen Gummibärchen. | *Erklären Sie das Zustandekommen der Unregelmäßigkeiten bei den geschmolzenen Gummibärchen. | ||
| + | :Das wurde gerade in der Aufgabe zum Mikrowellenherd erklärt. | ||
*Bestimmen Sie aus dem nebenstehenden Bild die Wellenlänge und die Frequenz der Mikrowellen. | *Bestimmen Sie aus dem nebenstehenden Bild die Wellenlänge und die Frequenz der Mikrowellen. | ||
| + | :Die geschmolzenen Gummibärchen lagen bei den Bäuchen und die unversehrten Gummibärchen bei den Knoten der stehenden Welle. Der Abstand zwischen zwei Bäuchen oder zwischen zwei Knoten beträgt ungefähr 10cm. Das entspricht der halben Wellenlänge. (Vgl. mit [[Eigenschwingungen von ausgedehnten Gegenständen ("Stehende Wellen")|mechanischen stehenden Wellen]].) | ||
| + | :Die Wellenlänge beträgt also ca. 20cm. | ||
=====Brechung von Mikrowellen===== | =====Brechung von Mikrowellen===== | ||
| − | Ein Mikrowellensender sendet elektromagnetische Wellen im cm-Bereich aus. Die Welle | + | Ein Mikrowellensender sendet elektromagnetische Wellen im cm-Bereich aus, die auf eine mit Sand gefüllte Schale in Dreiecksform treffen. Die Welle kann man vereinfachend als ebene Welle betrachten. |
*Zeichnen Sie den weiteren Verlauf der Wellenstrahlen qualitativ richtig ein und begründen Sie dies. | *Zeichnen Sie den weiteren Verlauf der Wellenstrahlen qualitativ richtig ein und begründen Sie dies. | ||
| + | :Im Sand breitet sich die Mikrowelle langsamer aus als in der Luft. An der Grenze zwischen den Materialien kommt es daher zur [[Reflektion und Brechung einer Welle|Brechung]] der Welle. | ||
| + | :Beim Eintritt in den Sand beträgt der Einfallswinkel Null Grad, daher ändert sich die Ausbreitungsrichtung nicht. | ||
| + | :Beim Austritt aus dem Sand vergrößert sich die Geschwindigkeit, weshalb die Welle vom Lot weg gebrochen wird. | ||
*Welche Angaben bräuchten Sie, um den Verlauf exakt einzuzeichnen? | *Welche Angaben bräuchten Sie, um den Verlauf exakt einzuzeichnen? | ||
[[Datei:Aufgabe_Mikrowellen_Brechung_Sand.png|512px]] | [[Datei:Aufgabe_Mikrowellen_Brechung_Sand.png|512px]] | ||
| − | + | :Die Ausbreitungsgeschwindigkeit in Luft kennt man, sie beträgt fast exakt Lichtgeschwindigkeit. Zusätzlich müßte man die Ausbreitungsgeschwindigkeit der Mikrowelle in Sand kennen. | |
===Radio=== | ===Radio=== | ||
| Zeile 62: | Zeile 79: | ||
*Erläutern Sie kurz das Prinzip des Radios mit dem Sender-Empfänger-Modell | *Erläutern Sie kurz das Prinzip des Radios mit dem Sender-Empfänger-Modell | ||
=====Wellenlängen===== | =====Wellenlängen===== | ||
| − | *UKW wird mit einer Frequenz von | + | *UKW wird mit einer Frequenz von 87,5MHz bis 108MHz gesendet, Mittelwelle von 526,5kHz bis 1606,5kHz. Das LTE-Handynetz arbeitet unter anderem mit einer Frequenz von 2GHz. |
:Berechnen Sie die jeweiligen Wellenlängen. | :Berechnen Sie die jeweiligen Wellenlängen. | ||
| + | :Dazu formt man den Zusammenhang zwischen Ausbreitungsgeschwindigkeit, (hier der Lichtgeschwindigkeit c=300.000km/s), der Wellenlänge und der Frequenz um: <math>c = \lambda \, f </math>. | ||
| + | :Also folgt für die Wellenlänge von UKW: | ||
| + | ::<math>\lambda = \frac{c}{f} = </math> | ||
| + | |||
=====Antennen===== | =====Antennen===== | ||
*Entwerfen Sie für den Empfang von Handywellen, UKW und MW eine passende Stabantenne. Erklären Sie die Funktionsweise der Antenne | *Entwerfen Sie für den Empfang von Handywellen, UKW und MW eine passende Stabantenne. Erklären Sie die Funktionsweise der Antenne | ||
Aktuelle Version vom 5. Dezember 2022, 12:09 Uhr
(Kursstufe > Elektromagnetische Schwingungen und Wellen)
Inhaltsverzeichnis
BAUSTELLE!!!
Elektromagnetische Schwingungen
Vergleich von elektrischer und mechanischer Schwingung
Vergleichen Sie einen elektrischen Schwingkreis mit einem horizontalen Federpendel mit Zeichnungen, einem erklärenden Text und einer Gegenüberstellung sich entsprechender Größen.
- Der Vergleich ist auf dieser Seite schön zu sehen.
Ein Schwingkreis
Ein Kondensator mit einer Kapazität von [math]54\,\rm \mu F[/math] wird mit einer Spannungsquelle von 50V verbunden und über eine Spule mit der Induktivität von 300H entladen.
- a) Wieviel Ladung und wieviel Energie ist zu Beginn im Kondensator gespeichert?
- b) Was kann man beobachten, wenn man die Spannung am Kondensator mißt?
- c) Warum geht die Spannung nach einiger Zeit dauerhaft auf Null Volt zurück?
- d) Mit welcher Frequenz ändert sich die Spannung?
- e) Wieviel Energie steckt maximal in der Spule?
- f) Wieviel Strom fließt maximal durch die Spule?
- g) Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der Spannung und der Stromstärke während der ersten 1,6 Sekunden.
Elektrische Wirbelfelder
Qual der Wahl
- Welche der Aussagen ist richtig?
- Generell gilt: Nur ein sich veränderndes Feld erzeugt ein Feld. Ein statisches Feld erzeugt kein anderes Feld.
- Finden Sie passende Experimente, Gedankenexperimente oder Alltagssituationen, welche Ihre Antworten begründen.
- a) Um ein sich änderndes Magnetfeld befindet sich immer ein elektrisches Wirbelfeld.
- Das ist richtig, man kann das mit der sogenannten "elektrodenlosen Ringentladung" experimentell zeigen.
- Auch bei allen Induktionsvesuchen kann man argumentieren, dass längs der Leiterschleife ein elektrisches Feld entstanden ist, das die Spannung hervorruft.
- b) Um ein elektrisches Feld befindet sich immer ein Magnetfeld.
- Nein, das ist falsch.
- c) Um ein Magnetfeld befindet sich immer eine elektrisches Feld.
- Nein, das ist falsch.
- d) Um ein sich änderndes elektrisches Feld befindet sich immer ein Magnetfeld.
- Ja, das stimmt, ist aber experimentell schwer direkt nachzuweisen. Der Gedankenversuch "Aufladen eines Kondensators" macht es zumindest plausibel.
Elektromagnetische Wellen
Feldlinienbild
- Zeichen Sie das Feldlinienbild einer ebenen elektro-magnetischen Welle.
- Das sieht man sich am besten in dieser Animation an.
- Die Feldlinien des Magnetfeldes und des elektrischen Feldes stehen immer aufeinander und zur Ausbreitungsrichtung senkrecht.
Wellenlänge und Frequenz
- Elektromagnetische Wellen haben, je nach Wellenlänge, unterschiedliche Namen bekommen. Nennen Sie verschiedene und sortieren Sie diese von langen zu kurzen Wellenlängen.
- Berechnen Sie die Wellenlänge bei einem Radar, dass mit einer Frequenz von 5 GHz arbeitet.
- Wie bei allen Wellen gibt es einen festen Zusammenhang zwischen Ausbreitungsgeschwindigkeit, (hier der Lichtgeschwindigkeit c=300.000km/s), der Wellenlänge und der Frequenz: [math]c = \lambda \, f [/math].
- Also folgt für die Wellenlänge:
- [math]\lambda = \frac{c}{f} = \frac{3\cdot 10^{8}\,\rm \frac{m}{s}}{5\cdot 10^{9}\,\rm Hz} = 0{,}06\,\rm m = 6\,\rm cm [/math]
- Berechnen Sie die Frequenz einer "roten Lichtwelle" mit einer Wellenlänge von 630 nm.
- Diesmal löst man nach der Frequenz auf:
- [math] f = \frac{c}{\lambda} = \frac{3\cdot 10^{8}\,\rm \frac{m}{s}}{630\cdot 10^{-9}\,\rm m} = 4{,}76\cdot 10^{14}\,\rm Hz = 476\,\rm T Hz[/math]
Mikrowellenherd
- Warum kann man in der Mikrowelle schlecht ein Brot erwärmen, aber sehr gut eine Suppe erhitzen?
- In Brot befindet sich, im Gegensatz zur Suppe, nur wenig Wasser. Eine Mikrowelle ist aber besonders darauf ausgelegt Wasser zu erhitzen. Die Wassermoleküle haben nämlich einen elektrischen Dipol und werden von dem elektrischen Wechselfeld ständig gedreht, wodurch sich die "innere Energie" der Speisen, also die Wärmeenergie erhöht.
- Warum haben Mikrowellen in der Regel einen Drehteller?
- Durch Reflektionen der Wellen an den Metallwänden und die Überlagerung mit den noch nicht reflektierten Wellen entsteht im Innenraum eine stehende, elektromagnetische Welle mit Knoten und Bäuchen. An den Bäuchen befindet sich ein besonders starkes Wechselfeld, bei den Knoten ein sehr schwaches. Ohne Drehteller würden die Speisen ungleichmäßig gewärmt.
Gummibärchen in der Mikrowelle
- Erklären Sie das Zustandekommen der Unregelmäßigkeiten bei den geschmolzenen Gummibärchen.
- Das wurde gerade in der Aufgabe zum Mikrowellenherd erklärt.
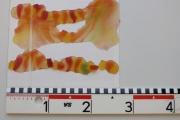
- Bestimmen Sie aus dem nebenstehenden Bild die Wellenlänge und die Frequenz der Mikrowellen.
- Die geschmolzenen Gummibärchen lagen bei den Bäuchen und die unversehrten Gummibärchen bei den Knoten der stehenden Welle. Der Abstand zwischen zwei Bäuchen oder zwischen zwei Knoten beträgt ungefähr 10cm. Das entspricht der halben Wellenlänge. (Vgl. mit mechanischen stehenden Wellen.)
- Die Wellenlänge beträgt also ca. 20cm.
Brechung von Mikrowellen
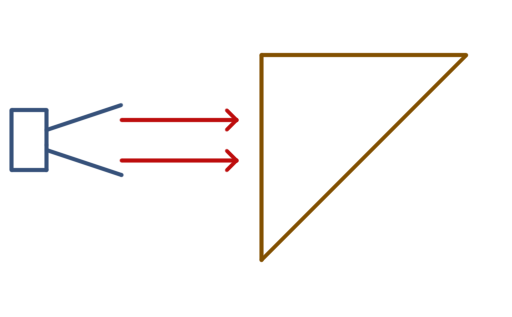
Ein Mikrowellensender sendet elektromagnetische Wellen im cm-Bereich aus, die auf eine mit Sand gefüllte Schale in Dreiecksform treffen. Die Welle kann man vereinfachend als ebene Welle betrachten.
- Zeichnen Sie den weiteren Verlauf der Wellenstrahlen qualitativ richtig ein und begründen Sie dies.
- Im Sand breitet sich die Mikrowelle langsamer aus als in der Luft. An der Grenze zwischen den Materialien kommt es daher zur Brechung der Welle.
- Beim Eintritt in den Sand beträgt der Einfallswinkel Null Grad, daher ändert sich die Ausbreitungsrichtung nicht.
- Beim Austritt aus dem Sand vergrößert sich die Geschwindigkeit, weshalb die Welle vom Lot weg gebrochen wird.
- Welche Angaben bräuchten Sie, um den Verlauf exakt einzuzeichnen?
- Die Ausbreitungsgeschwindigkeit in Luft kennt man, sie beträgt fast exakt Lichtgeschwindigkeit. Zusätzlich müßte man die Ausbreitungsgeschwindigkeit der Mikrowelle in Sand kennen.
Radio
Sender-Empfänger-Modell
- Erläutern Sie kurz das Prinzip des Radios mit dem Sender-Empfänger-Modell
Wellenlängen
- UKW wird mit einer Frequenz von 87,5MHz bis 108MHz gesendet, Mittelwelle von 526,5kHz bis 1606,5kHz. Das LTE-Handynetz arbeitet unter anderem mit einer Frequenz von 2GHz.
- Berechnen Sie die jeweiligen Wellenlängen.
- Dazu formt man den Zusammenhang zwischen Ausbreitungsgeschwindigkeit, (hier der Lichtgeschwindigkeit c=300.000km/s), der Wellenlänge und der Frequenz um: [math]c = \lambda \, f [/math].
- Also folgt für die Wellenlänge von UKW:
- [math]\lambda = \frac{c}{f} = [/math]
Antennen
- Entwerfen Sie für den Empfang von Handywellen, UKW und MW eine passende Stabantenne. Erklären Sie die Funktionsweise der Antenne
- Wieso besteht eine Mittelwellen-Empfangsantenne aus einer Spule mit einem Ferritkern und eine UKW-Antenne aus einem Metallstab?
Empfangsqualität
- Wieso ändert sich der Empfang eines Radios mit dem Ort und der Ausrichtung der Antenne?
Antennenausrichtung
Ein Mittelwellensender sendet mit einer senkrecht zum Boden ausgerichteten Stabantenne.
- Wie muss man die Ferrit-Antenne ausrichten, damit man guten Empfang hat?
- (Wie müßte man bei einem UKW-Sender mit senkrechter Antenne die Stabantenne ausrichten?)
AM & FM
- Was bedeutet "AM" und was bedeutet "FM"?
Senderwechsel
- Wie erreicht man es, dass man bei einem Radio den Sender wechseln kann?