Gleichmäßig beschleunigte Bewegung mit konstanter Impulsänderung: Unterschied zwischen den Versionen
(→Bewegungsgesetze der gleichförmigen und gleichmäßig beschleunigten Bewegung) |
(→Bewegungsgesetze der gleichförmigen und gleichmäßig beschleunigten Bewegung) |
||
| Zeile 106: | Zeile 106: | ||
*Zusammenfassung mit s0 v0 a=F/m | *Zusammenfassung mit s0 v0 a=F/m | ||
| + | ===Bewegungsgesetze der gleichförmigen Bewegung=== | ||
| + | ===Bewegungsgesetze der gleichmäßig beschleunigten Bewegung=== | ||
| + | {| | ||
| + | !Bewegungsgesetze | ||
| + | !Bewegungsdiagramme | ||
| + | |- | ||
| + | | | ||
{|class="wikitable" style="text-align: left; " | {|class="wikitable" style="text-align: left; " | ||
|style="border-style: solid; border-width: 5px "| | |style="border-style: solid; border-width: 5px "| | ||
| Zeile 132: | Zeile 139: | ||
Kraft | Kraft | ||
| − | <math>F=F_0</math> | + | <math>F(t) = F_0</math> |
| + | |||
| + | |} | ||
| + | |||
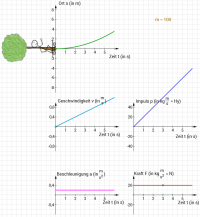
| + | |[[Datei:Bewegungsdiagramme_gleichmäßig_beschleunigte_Bewegung.png|200px]] | ||
|} | |} | ||
Version vom 8. Januar 2015, 10:23 Uhr
Wer war Schuld? (Verschiedene Unfallspuren)
War der Sicherheitsabstand ausreichend? (Bremsverzögerungswerte auf verschiedenem Untergrund)
Inhaltsverzeichnis
Gleichförmige Bewegung: konstante Impulsmenge
Kennzeichen ist die gleiche Impulsmenge. Entweder weil kein Kraft wirkt, also auch kein Impuls rein oder raus geht. Oder weil die Kraftsumme Null ist, also genausoviel Impuls dazukommt wie weggeht. (Vgl. Gleichförmige Bewegung mit konstantem Impuls (Kräftegleichgewicht; Fließgleichgewicht))
Gleichmäßig beschleunigte Bewegung: konstante Impulszu- oder abnahme
Versuch: Ein Wagen rollt berab
- Aufbau
Ein kleiner Wagen wird auf eine schräggestellte Schiene gesetzt und losgelassen. Am Ende der Schiene bremst etwas Knete den Wagen.
Mit Hilfe eines Ultraschallsensors kann dabei der Ort des Wagens bestimmt werden, wobei das Ortskoordinatensystem gerade die Schiene selbst ist. Den Nullpunkt kann man beliebig setzen, z.B. an den linken Rand der Schiene.
- Messung
- Ergebnis
- Im Wasserbehältermodell
Die gefundene gleichmäßige Zunahme von Impuls und Geschwindigkeit ist nicht überraschend. Eine konstante Kraft entspricht im Wasserbehältermodell einer gleichmäßigen Zunahme der Wassermenge (Impuls) und damit auch der Wasserhöhe (Geschwindigkeit).
Das Modell kann allerdings keine Aussagen über den Ort des Wagens machen!
- Zahlenwerte
Das Impulsdiagramm liefert folgendes:
- Der Impuls hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,04 Hy.
- Die Impulszunahme, also die Kraft, war in etwa konstant. Sie entspricht der Steigung im Diagramm und beträgt
- [math]F=\frac{\triangle p}{\triangle t}=\frac{0{,}04\rm Hy}{2{,5}\rm s} = 0{,}016\rm N[/math]
- Die Hangabtriebskraft war also um 0,016 Newton größer als die Reibungskraft. Das ist nicht viel und entspricht der Gewichtskraft von 1,6 Gramm.
- Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s sinkt die Impulsmenge um 0,04Hy. Ausserdem war die Kraft, also die Impulsänderung, beim Bremsen nicht konstant. Die mittlere Kraft entspricht der mittleren Steigung und betrug
- [math]\bar F=\frac{-0{,}04\rm Hy}{0{,}2\rm s} = -0,2\rm N[/math]
- Man hätte den Wagen also mit einer Kraft von 0,2 Newton, die 0,2 Sekunden lang wirkt abbremsen können.
Das Kraftdiagramm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.
- Die Fläche unter dem Diagramm entspricht der Impulsänderung.
- Während der Beschleunigung kommen ca. 0,04 Hy dazu, beim Abbremsen sinkt die Impulsmenge wieder auf Null.
Am Ortsdiagramm kann man folgendes ablesen:
- Der Wagen befindet sich zunächst am Anfang der Schiene. Nach ca. zwei Sekunden wurde er losgelassen und erreicht den Knetklumpen nach ca. 4,5 Sekunden. Während seiner Fahrt wurde er immer schneller. Der Knetklumpen lag 0,6m vom linken Rand entfernt.
Das Geschwindigkeitsdiagramm liefert folgendes:
- Die Geschwindigkeit hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,4 m/s.
- Die Beschleunigung beim Bergabrollen war also in etwa konstant. Sie beträgt
- [math]a=\frac{0{,}4\rm\frac{m}{sec}}{2{,5}\rm s} = 0{,}16\rm \frac{m}{s^2}[/math]
- Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s fiel die Geschwindigkeit um 0,4m/sec. Ausserdem war die Beschleunigung beim Bremsen nicht konstant. Die mittlere Beschleunigung betrug
- [math]\bar a=\frac{-0{,}4\rm\frac{m}{s}}{0{,}2\rm s} = -2\rm \frac{m}{s^2}[/math]
Das Beschleunigungsdiagamm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.
Bewegungsgesetze herleiten
Die folgenden Aufgaben kann man mit dieser Animation der Bewegungsdiagramme lösen!
Pauline und Paul fahren Skateboard. Pauline ist kleiner und bringt deshalb nur 50kg auf die Waage im Vergleich zu doppelt so schweren Paul.
konstanter Impuls und Geschwindigkeit
Pauline fährt mit konstanter Geschwindigkeit von 1 m/s. Als sie am Baum vorbeifährt, beginnt die Zeitmessung. Die Reibung soll zunächst vernachlässigt werden.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wo ist Pauline nach 6 Sekunden und wie schnell ist sie?
- c) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
- [math]s(t) = v\, t = 1 \, \rm{\frac{m}{s}} \cdot t[/math]
- [math]v(t) = v_0 = 1 \, \rm \frac{m}{s} [/math]
- [math]a(t) = 0 \, \rm \frac{m}{s^2}[/math]
- d) Löse b) mit Hilfe der Bewegungsgesetze.
konstante Impuls- und Geschwindigkeitszunahme
Pauline steht zu Beginn am Baum. Dann wird sie von Paul mit 20 Newton angeschoben.
- Vernachläßige zunächst die auftretende Reibung.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wieviel Impuls hat Pauline 1s, 2s,... nach dem Start?
- c) Wie schnell ist sie 1s, 2s,... nach dem Start?
- d) Wie weit fährt sie innerhalb von 1s, 2s,... nach dem Start?
- e) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
- [math]s(t) = \frac{1}{2} \, a\, t^2 = 0{,}2 \, \rm \frac{m}{s^2} \cdot t^2[/math]
- [math]v(t) = a\, t = 0{,}4 \, \rm \frac{m}{s^2} \cdot t[/math]
- [math]a(t) = \frac{F}{m} = 0{,}4 \, \rm \frac{m}{s^2}[/math]
- f) Löse c) und d) mit Hilfe der Bewegungsgesetze.
- g) Nun tauschen Paul und Pauline die Rollen: Er steht am Baum auf dem Board und sie zieht mit 20 Newton. Vergleiche seine Fahrt mit der von Pauline.
- h) Nimm nun an, dass bei Pauline eine Reibungskraft von 5N und bei Paul von 10N wirkt, solange sie fahren. Wie verändert sich die Fahrt der beiden?
Bremswege
Pauline kommt mit 1 m/s angerauscht. Als sie am Baum vorbeifährt, sieht sie 2 Meter vor sich "Momo", die Katze der Nachbarn, sitzen. Sie bremst ab sofort mit 15 Newton, dazu kommen noch 5 Newton Reibungskraft.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wie lange dauert es, bis sie steht? Schafft sie es noch vor der Katze anzuhalten? Wenn nicht, bei welcher Geschwindigkeit kollidieren die beiden?
- c) Begründe folgende Formeln für die Bremszeit und den Bremsweg:
- [math]t_{brems} = \frac{m}{F} \, v_0 [/math]
- [math]s_{brems} = \frac{1}{2}\, \frac{m}{F}\, v_0^2[/math]
- d) Wie verändert sich der Bremsweg und die Bremszeit, wenn sich die Ausgangsgeschwindigkeit verdoppelt oder halbiert?
Bewegungsgesetze der gleichförmigen und gleichmäßig beschleunigten Bewegung
- Zusammenfassung mit s0 v0 a=F/m