Aufgaben zu Schwingungen (Lösungen): Unterschied zwischen den Versionen
(→6 Energie(f)) |
(→13) Schwingmännchen III) |
||
| (104 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanische Schwingungen|''' Mechanische Schwingungen''']]) | |
| − | [[ | + | |
| − | [[ | + | |
| − | + | ||
| − | + | *[[Aufgaben_zu_Schwingungen|'''Zurück zu den Aufgaben''']] | |
| − | + | ||
| − | ==== | + | ====1) Energieformen==== |
| − | + | Beispiele sind im Abschnitt "[[Grundbegriffe_und_Beispiele_von_Schwingungen#Beispiele|Grundbegriffe von Schwingungen]]" zu finden. | |
| − | ==== | + | |
| − | * | + | ====2) Schaukeltier==== |
| − | * | + | Das kann man im Abschnitt "[[Grundbegriffe_und_Beispiele_von_Schwingungen#Begriffe_einer_mechanischen_Schwingung|Begriffe einer mechanischen Schwingung]]" nachlesen. |
| − | * | + | |
| − | ==== | + | ====3) Zeigermodell==== |
| − | + | Der Versuch ist im Wiki unter im Kapitel [[Beschreibung_einer_harmonischen_Schwingung_mit_der_Zeigerdarstellung#Versuch: Projektion der Kreisbewegung|Zeigerdarstellung]] beschrieben, oder im Heft. | |
| − | + | ||
| − | ====Schwingmännchen II==== | + | ====4) Uhrzeiger==== |
| − | * | + | *Die Winkelgeschwindigkeit gibt an welcher Winkel in welcher Zeit überstrichen wird. Beim Sekundenzeiger eben 360° oder <math>2 \,\pi</math> in einer Minute. |
| − | * | + | |
| − | *die | + | *Die Periodendauer beträgt 60s und die Frequenz 1/60 Hz. |
| + | |||
| + | *Die Winkelgeschwindigkeit entspricht der Geschwindigkeit der Zeigerspitze bei einem Radius von 1. | ||
| + | :Verzehnfacht man den Radius, so verzehnfacht sich auch die Geschwindigkeit: <math>v=\omega \, r = \frac{2\,\pi}{60\,s}\cdot 10\,\rm cm = 1{,}05 \frac{cm}{s}</math> | ||
| + | |||
| + | ====5) Schwingmännchen==== | ||
| + | *Der Zeiger hat eine Länge von 3cm. | ||
| + | <gallery widths=150px heights=130px perrow=4 > | ||
| + | Bild:Aufgabe_Schwingung_Zeiger_t0-25.png|<math>t= 0{,}25\, s</math> eine halbe Periode ist vorbei, <math>y=0\,\rm cm</math>.<math></math> | ||
| + | Bild:Aufgabe_Schwingung_Zeiger_t0-125.png|<math>t = 0{,}125\, s</math> eine viertel Periode ist vorbei, <math>y=3\,\rm cm</math>. | ||
| + | Bild:Aufgabe_Schwingung_Zeiger_t0-4375.png|<math>t = 0{,}4375\, s</math> 7/8 der Periode sind vorbei, <math>y=-2{,}1\,\rm cm</math>. | ||
| + | </gallery> | ||
| + | |||
| + | ====6) Stimmgabel==== | ||
| + | *<math>T=\frac{1}{f}=\frac{1}{440\, \rm 1/s} = 0{,}00227\, \rm s</math> | ||
| + | :<math>\omega = 2\,\pi\,f = 2760\, \rm Hz</math> | ||
| + | |||
| + | *<math>y(t)=2 \,\rm mm \cdot \sin (2760\,\rm Hz \cdot t)</math> | ||
| + | :<math>v(t)=5520 \,\rm mm/s \cdot \cos (2760\,\rm Hz \cdot t) = 5{,}52 \,\rm m/s \cdot \cos (2760\,\rm Hz \cdot t) </math> | ||
| + | :<math>a(t)=-15200 \,\rm m/s^2 \cdot \sin (2760\,\rm Hz \cdot t)</math> | ||
| + | |||
| + | *Maximale Geschwindigkeit: <math>\hat v = 5{,}52 \,\rm m/s \approx 20 \, \rm km/h</math> | ||
| + | :Maximale Beschleunigung: <math>\hat a = 15200 \,\rm m/s^2</math> (Das ist das 1500-fache der Erdbeschleunigung!) | ||
| + | |||
| + | ====7) Horizontales Federpendel==== | ||
| + | *Die maximale Auslenkung (und die maximale Geschwindigkeit) des Wagens bleibt konstant, daher geht keine Energie aus der Schwingung heraus. | ||
| + | |||
| + | *Zu Beginn (t=0s) befindet sich der Wagen in der Ruhelage (y=0m) und wird mit 1m/s nach rechts angeschubst. | ||
| + | |||
| + | *Der Wagen bleibt in den äußeren Umkehrpunkten stehen und ist beim Durchgang durch die Ruhelage besonders schnell. Bleibt der Wagen z.B. im linken Umkehrpunkt stehen, so wirkt auf ihn eine Kraft nach rechts, die Geschwindigkeit nach rechts nimmt zu. Bis zur Ruhelage wird der Wagen weiter beschleunigt, danach wird er wieder abgebremst, weil die Rückstellkraft nun nach links wirkt. | ||
| + | :Die Auslenkung des Wagens hinkt der Geschwindigkeit des Wagens dabei um eine Viertel Schwingung hinterher: | ||
| + | :{|class="wikitable" | ||
| + | ||t=0 || v maximal, positiv || y=0 | ||
| + | |- | ||
| + | ||t=1/4 T || v=0 || y maximal, positiv | ||
| + | |- | ||
| + | ||t=1/2 T || v maximal, negativ ||y=0 | ||
| + | |- | ||
| + | ||t=3/4 T || v=0 ||y maximal, negativ | ||
| + | |- | ||
| + | ||t=T || v maximal, negativ ||y=0 | ||
| + | |} | ||
| + | :Die Beschleunigung hat die gleiche Richtung wie die Kraft. Da für die Rückstellkraft <math>F = -D\, y</math> gilt, ist auch die Beschleunigung immer entgegengesetzt zur Auslenkung. | ||
| + | |||
| + | *Aus dem Graphen der Auslenkung y kann man die Periodendauer von drei Sekunden ablesen: <math>T = 3 \, \rm s</math>. Also folgt für die Winkelgeschwindigkeit: | ||
| + | :<math>\omega = 2\pi \, f = \frac{2\pi}{T}\approx 2\,\rm Hz</math> | ||
| + | Aus der Winkelgeschwindigkeit und der Amplitude kann man nun die maximale Geschwindigkeit und Beschleunigung berechnen: | ||
| + | :<math>\hat v = \hat y\, \omega = 0{,}5\,\rm m \cdot 2\, \rm Hz = 1\, \rm m/s</math> | ||
| + | :<math>\hat a = \hat y\, \omega^2 = 0{,}5\,\rm m \cdot (2\, \rm Hz)^2 = 2\, \rm m/s^2</math> | ||
| + | :Die so berechneten Werte stimmen mit den an den Graphen ablesbaren Werten gut überein. Die maximale Beschleunigung ist dort etwas größer als 2m/s<sup>2</sup>, wahrscheinlich ist die Periodendauer etwas kleiner als die abgelesenen drei Sekunden. | ||
| + | :Auch an den Steigungen der Graphen kann man das Ergebnis kontrollieren: Die maximale Steigung des Graphen der Auslenkung beträgt tatsächlich gerade 1m/s, die maximale Steigung des Graphen der Geschwindigkeit ist tatsächlich 2m/s<sup>2</sup>. | ||
| + | |||
| + | ====8) Schwingmännchen II==== | ||
| + | *Wie groß sind Amplitude, Frequenz und Periodendauer? | ||
| + | :<math>\hat y = 5\,\rm cm</math> | ||
| + | :<math>2 \, \Pi \ f = 3 \,\rm Hz \Rightarrow f \approx 0{,}48 \,\rm Hz</math> | ||
| + | :<math>T=\frac{1}{f}\approx 2{,}1 \,\rm s</math> | ||
| + | |||
| + | *Zeichnen Sie das Ortsdiagramm, das Geschwindigkeitsdiagramm und das Beschleunigungsdiagramm jeweils in ein Koordinatensystem. | ||
| + | |||
| + | Die Geschwindigkeit und die Beschleunigung ergeben sich als erste und zweite Ableitung der Auslenkung: | ||
| + | |||
| + | :<math>v(t)=\dot y(t)=5 \, \rm cm \ 3 \,\rm Hz \cos(3\, \rm Hz \ t) = 15 \,\rm cm/s \cos(3 \,\rm Hz \ t)</math> | ||
| + | :<math>a(t)=\dot v(t)= -15 \,\rm cm/s\cdot 3\,\rm Hz \sin(3 \,\rm Hz \ t) = \dot v(t)= -45 \,\rm cm/s^2 \sin(3 \,\rm Hz \ t)</math> | ||
| + | |||
| + | Das kann man nun zeichnen. | ||
| + | |||
| + | *Zeichen Sie zum Ortsdiagramm die Zeiger für die Zeitpunkte t=0s, t=0,25s und t=1s. | ||
| + | Der Zeiger hat am Anfang (<math>t = 0 \,\rm s</math>) den Drehwinkel <math>\alpha = 0</math>. | ||
| + | Danach gilt : <math>\alpha = \omega \, t</math> | ||
| + | |||
| + | Für <math>t = 0{,}25 \,\rm s\: \qquad \alpha = 3\,\rm Hz \cdot 0{,}25\,\rm s= 0{,}75 = 0{,}75 \cdot \frac{180^\circ}{\pi}= 43^\circ</math> | ||
| + | |||
| + | [[Datei:Schwingung_Aufgabe_SchwingmännchenIV_Zeiger_t0.png|419px]] | ||
| + | [[Datei:Schwingung_Aufgabe_SchwingmännchenIV_Zeiger_t025.png|419px]] | ||
| + | [[Datei:Schwingung_Aufgabe_SchwingmännchenIV_Zeiger_t1.png|419px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
*Wo ist das Männchen nach 1,6 Sekunden und wie schnell ist es? | *Wo ist das Männchen nach 1,6 Sekunden und wie schnell ist es? | ||
| − | :<math>y(1,6 | + | :<math>y(1{,}6 \,\rm s) = 5 \,\rm cm \sin(3 \,\rm Hz 1{,}6 \,\rm s) \approx 5 \,\rm cm \ (-1) = -5 \,\rm cm</math> |
:Das Männchen ist fast am unteren Umkehrpunkt! | :Das Männchen ist fast am unteren Umkehrpunkt! | ||
| − | :<math>v(t)=\dot y(t)=5 cm \ 3 Hz \cos(3 Hz \ t) = 15 \ | + | :<math>v(t)=\dot y(t)=5 \,\rm cm \ 3 \,\rm Hz \cos(3 \,\rm Hz \ t) = 15 \,\rm cm/s \cos(3 \,\rm Hz \ t)</math> |
| − | :<math>v(1,6 | + | :<math>v(1{,}6 \,\rm s)=15 \,\rm cm/s \cos(3 \,\rm Hz \ 1{,}6 \,\rm s) \approx 15 \,\rm cm/s \cdot 0{,}1 = 1{,}5 \,\rm cm/s </math> |
:Dort bleibt es annähernd stehen. | :Dort bleibt es annähernd stehen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
*Wie schnell ist das Männchen maximal? | *Wie schnell ist das Männchen maximal? | ||
| − | :<math>\hat v = 15 \ | + | :<math>\hat v = 15 \,\rm cm/s </math> |
| − | ====Energie==== | + | ====9) Messungen an einem Federpendel==== |
| + | An eine Feder wird ein Gewichtsstück gehängt und zum Schwingen gebracht. In einem Experiment soll untersucht werden wovon die Periodendauer dieses Federpendels abhängt. | ||
| + | |||
| + | :'''a)''' Nennen Sie mögliche Größen, von denen die Periodendauer abhängen könnte. | ||
| + | :Die Periodendauer könnte von allen möglichen Faktoren abhängen: Masse des Gewichtsstücks, Härte der Feder, maximale Auslenkung der Schwingung, Erdbeschleunigung, Breite des Gewichtsstücks, Luftdruck, Lufttemperatur, Masse der Feder, Material der Feder, Uhrzeit, Mondphase, Sonnenaktivität, ... | ||
| + | :'''b)''' Beschreiben Sie wie man die Messungen durchführen muss, damit man diese Abhängigkeiten untersuchen kann. | ||
| + | :Man muss eine der Größen variieren und alle anderen Einflussfaktoren dabei konstant halten. | ||
| + | :'''c)''' Die folgenden Tabellen zeigen die Messergebnisse von drei Versuchsreihen. Bestimmen Sie zunächst rechnerisch von welchen Größen die Periodendauer abhängt und von welchen nicht. Berechnen Sie dann eine Formel für die Periodendauer in Abhängigkeit von den entsprechenden Größen. | ||
| + | :'''d)''' Zeigen Sie durch eine Rechnung, dass für das Federpendel der Zusammenhang <math>\omega^2 = \frac{D}{m}</math> gilt. | ||
| + | :[[Datei:Aufgabe_Federschwingung_Messung_auswerten_Pseudodaten.png|300px]] | ||
| + | |||
| + | ====10) DGL ==== | ||
| + | [[Datei:Schwingungen Wagen an Feder.png|thumb|280px]] | ||
| + | Ein Wagen ist mit einer Feder an einem Tisch befestigt. (Siehe Abbildung) | ||
| + | <br>Für diese Situation hat man folgende Differentialgleichung aufgestellt: | ||
| + | :<math>0{,}1\,{\rm kg}\,\cdot \ddot y(t) = -0{,}4\,{\rm\tfrac{N}{m}} \cdot y(t)</math> | ||
| + | |||
| + | '''a)''' Erläutern Sie die Gleichung. | ||
| + | *Die Variable y(t) beschreibt den Ort des Wagens im Koordinatensystem in Abhängigkeit von der Zeit, also das Ort-Zeit-Gesetz der Bewegung des Wagens. | ||
| + | *Die rechte Seite der Gleichung gibt an welche Kraft auf den Wagen im Ort y wirkt. Die Feder ist am Ort y=0m entspannt, dort wirkt keine Kraft. Wird die Feder um die Strecke y zusammengedrückt oder verlängert, so wirkt eine zur Längenveränderung proportionale Kraft. Die Feder erfüllt offensichtlich das Hooksche Gesetz mit der Federhärte 0,4 Newton pro Meter. Das Minuszeichen gibt an, dass bei einem Ort rechts vom Ursprung die Kraft nach links wirkt und umgekehrt. | ||
| + | *Die linke Seite der Gleichung beschreibt welche Beschleunigung aus der wirkenden Kraft resultiert. Denn es gilt: <math>F=m\,a</math>, wobei die Beschleunigung a die zweite zeitliche Ableitung des Ortes y ist. | ||
| + | *Alle Lösungen <math>y(t)</math> der DGL beschreiben Bewegungen, die von diesem physikalischen System ausgeführt werden können. Ein Ortsgesetz <math>y(t)</math>, welches keine Lösung der DGL ist, beschreibt eine Bewegung, die der Wagen nicht ausführen kann. | ||
| + | |||
| + | '''b)''' Untersuchen Sie welche der nachfolgenden Funktionen eine Lösung der DGL ist: | ||
| + | |||
| + | *Zuerst berechnet man die zweite zeitliche Ableitung der Ortsfunktion. Die Änderung von Metern ist Meter pro Sekunde und deren Änderung ist Meter pro Sekunde im Quadrat: | ||
| + | :<math>y_1(t)=0\,{\rm m} \quad \Rightarrow \quad \ddot y_1(t) = 0\,{\rm\tfrac{m}{s^2}}</math> | ||
| + | :Die Ortsfunktion und ihre zweite Ableitung kann man nun in die DGL einsetzen und überprüfen, ob die Gleichung stimmt: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && 0{,}1\,{\rm kg}\,\cdot 0\,{\rm\tfrac{m}{s^2}} &= -0{,}4\,{\rm\tfrac{N}{m}} \cdot 0\,{\rm m}\\ | ||
| + | \Leftrightarrow | ||
| + | && 0\,{\rm kg\,\tfrac{m}{s^2}} &= 0\,{\rm N}\\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist wahr! Das Ortsgesetz <math>y_1(t)</math> ist also eine Lösung der DGL. | ||
| + | :Anschaulich bedeutet das, dass der Wagen in der Ruhelage stehen bleiben kann, was einleuchtet, denn dort wirkt keine Kraft auf ihn. | ||
| + | |||
| + | *<math>y_2(t)=0{,}01\,{\rm m} \quad \Rightarrow \quad \ddot y_1(t) = 0\,{\rm\tfrac{m}{s^2}}</math> | ||
| + | :In die DGL einsetzen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && 0{,}1\,{\rm kg\,\cdot 0\,\rm\tfrac{m}{s^2}} &= -0{,}4\,{\rm\tfrac{N}{m}} \cdot 0{,}01\,{\rm m}\\ | ||
| + | \Leftrightarrow | ||
| + | && 0\,{\rm kg\,\tfrac{m}{s^2}} &= -0{,}004\,{\rm N}\\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist nicht wahr! Das Ortsgesetz <math>y_2(t)</math> ist keine Lösung der DGL. | ||
| + | :Anschaulich bedeutet das, dass der Wagen einen Zentimeter rechts von der Ruhelage nicht stehen bleiben kann. Das leuchtet ein, denn dort wirkt eine Rückstellkraft von <math>0{,}004\,\rm N</math> nach links auf ihn. | ||
| + | |||
| + | *<math>y_3(t)=0{,}01\,{\rm m} \cdot \sin(1\,{\rm Hz}\cdot t) \quad \Rightarrow \quad \dot y_3(t) = 0{,}01\,{\rm m}\cdot 1\,{\rm Hz}\cdot \cos(1\,{\rm Hz}\cdot\,t) \quad \Rightarrow \quad \ddot y_3(t) = -0{,}01\,{\rm m\,Hz^2}\cdot \sin(1\,{\rm Hz}\cdot\,t) </math> | ||
| + | :In die DGL einsetzen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && -0{,}1\,{\rm kg}\cdot 0{,}01\,{\rm m\,Hz^2}\cdot \sin(1\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}01\,{\rm m} \cdot \sin(1\,{\rm Hz}\cdot t) \\ | ||
| + | \Leftrightarrow | ||
| + | && -0{,}001\,{\rm kg\,\tfrac{m}{s^2}}\cdot \sin(1\,{\rm Hz}\cdot\,t) &= -0{,}004\,{\rm N} \cdot \sin(1\,{\rm Hz}\cdot t) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist nicht wahr! Das Ortsgesetz <math>y_3(t)</math> ist keine Lösung der DGL. | ||
| + | :Der Wagen kann also nicht mit einer Amplitude von 1cm und einer Periodendauer von <math>T=2\pi\,{\rm s}\approx 6\,{\rm s}</math> schwingen. | ||
| + | |||
| + | *<math>y_4(t)=0{,}01\,{\rm m} \cdot \sin(2\,{\rm Hz}\cdot t) \quad \Rightarrow \quad \dot y_4(t) = 0{,}01\,{\rm m}\cdot 2\,{\rm Hz}\cdot \cos(2\,{\rm Hz}\cdot\,t) \quad \Rightarrow \quad \ddot y_4(t) = -0{,}04\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) </math> | ||
| + | :In die DGL einsetzen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && -0{,}1\,{\rm kg}\cdot 0{,}04\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}01\,{\rm m} \cdot \sin(2\,{\rm Hz}\cdot t) \\ | ||
| + | \Leftrightarrow | ||
| + | && -0{,}004\,{\rm kg\,\tfrac{m}{s^2}}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}004\,{\rm N} \cdot \sin(2\,{\rm Hz}\cdot t) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist wahr! Das Ortsgesetz <math>y_4(t)</math> ist eine Lösung der DGL. | ||
| + | :Der Wagen kann also mit einer Amplitude von 1cm und einer Periodendauer von <math>T=\pi\,{\rm s}\approx 3\,{\rm s}</math> harmonisch schwingen. | ||
| + | |||
| + | *<math>y_5(t)=0{,}01\,{\rm m} \cdot \cos(2\,{\rm Hz}\cdot t) \quad \Rightarrow \quad \ddot y_5(t) = -0{,}04\,{\rm m\,Hz^2}\cdot \cos(2\,{\rm Hz}\cdot\,t) </math> | ||
| + | :In die DGL einsetzen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && -0{,}1\,{\rm kg}\cdot 0{,}04\,{\rm m\,Hz^2}\cdot \cos(2\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}01\,{\rm m} \cdot \cos(2\,{\rm Hz}\cdot t) \\ | ||
| + | \Leftrightarrow | ||
| + | && -0{,}004\,{\rm kg\,\tfrac{m}{s^2}}\cdot \cos(2\,{\rm Hz}\cdot\,t) &= -0{,}004\,{\rm N} \cdot \cos(2\,{\rm Hz}\cdot t) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist wahr! Das Ortsgesetz <math>y_5(t)</math> ist eine Lösung der DGL. | ||
| + | :Im Unterschied zu <math>y_4(t)</math> beginnt die Bewegung mit einer maximalen Auslenkung. Der Wagen wird also 1cm nach rechts ausgelenkt und bei <math>t=0\,\mathrm s</math> losgelassen. | ||
| + | |||
| + | *<math>y_6(t)=0{,}05\,\mathrm{cm} \cdot \sin(2\,{\rm Hz}\cdot\,t) \quad \Rightarrow \quad \ddot y_6(t) = -0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) </math> | ||
| + | :In die DGL einsetzen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && -0{,}1\,{\rm kg}\cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}05\,{\rm m} \cdot \sin(2\,{\rm Hz}\cdot t) \\ | ||
| + | \Leftrightarrow | ||
| + | && -0{,}02\,{\rm kg\,\tfrac{m}{s^2}}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}02\,{\rm N} \cdot \sin(2\,{\rm Hz}\cdot t) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist wahr! Das Ortsgesetz <math>y_6(t)</math> ist eine Lösung der DGL. | ||
| + | :Der Wagen kann also mit einer Amplitude von 5cm und einer Periodendauer von <math>T=\pi\,{\rm s}\approx 3\,{\rm s}</math> harmonisch schwingen. | ||
| + | |||
| + | |||
| + | *<math>y_7(t)=5\,\rm cm \cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) \quad \Rightarrow \quad \ddot y_6(t) = -0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) </math> | ||
| + | :In die DGL einsetzen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | && -0{,}1\,{\rm kg}\cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}05\,{\rm m} \cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4})\\ | ||
| + | \Leftrightarrow | ||
| + | && -0{,}02\,{\rm kg\,\tfrac{m}{s^2}}\cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) &= -0{,}02\,{\rm N} \cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | :Diese Aussage ist wahr! Das Ortsgesetz <math>y_7(t)</math> ist eine Lösung der DGL. | ||
| + | :Der Wagen schwingt harmonisch mit einer Amplitude von 5cm und einer Periodendauer von <math>T=\pi\,{\rm s}\approx 3\,{\rm s}</math>. Durch die Addition von <math>\tfrac{2\pi}{4}</math> wird der [[Beschreibung_einer_harmonischen_Schwingung_mit_der_Zeigerdarstellung#Die_Zeigerdarstellung|Zeiger]] zusätzlich um 90° gedreht, wodurch die Bewegung mit maximaler Auslenkung nach rechts beginnt, genau so wie bei <math>y_5(t)</math>. Das ergibt sich auch aus dem mathematischen Zusammenhang: <math>\sin(t+\tfrac{2\pi}{4})=\cos(t)</math>. | ||
| + | |||
| + | |||
| + | '''c)''' Erläutern Sie die physikalische Bedeutung der rechnerischen Ergebnisse von b). | ||
| + | :Steht bereits oben bei b). | ||
| + | |||
| + | Die DGL für die speziellen Werte von Masse und Federhärte kann man verallgemeinern: | ||
| + | :<math>m \, \ddot y(t) = - D \, y(t)</math> | ||
| + | |||
| + | '''d)''' Leiten Sie daraus die Formel für die Periodendauer des schwingenden Wagens ab: | ||
| + | :<math>T = 2 \pi \sqrt{\frac{m}{D}}</math> | ||
| + | *Als mögliche Lösung nimmt man eine harmonische Schwingung mit einer beliebigen Amplitude <math>\hat y</math> und einer beliebigen Kreisfrequenz <math>\omega</math> und setzt sie in die DGL ein: | ||
| + | ::<math> y(t)=\hat y \, \sin(\omega \,t) \quad \Rightarrow \quad \ddot y(t) = -\hat y \,\omega^2 \,\sin(\omega t)</math> | ||
| + | ::<math>m \,\omega^2 \hat y \, \sin(\omega \,t) = - D \, \hat y \, \sin(\omega \,t)</math> | ||
| + | :Man sieht, dass die Gleichung nur dann stimmt, wenn <math>m \,\omega^2 = D </math> gilt. Das kann man noch umformen und nach <math>T</math> auflösen: | ||
| + | |||
| + | :<math> | ||
| + | \begin{align} | ||
| + | &&m \,\omega^2 = D &&|:m\\ | ||
| + | \Leftrightarrow | ||
| + | &&\omega^2 = \frac{D}{m} &&& \textrm{mit }\omega=\frac{2\pi}{T}\\ | ||
| + | \Leftrightarrow | ||
| + | &&\left(\frac{2\pi}{T}\right)^2 = \frac{4\pi^2}{T^2} = \frac{D}{m} \\ | ||
| + | \Leftrightarrow | ||
| + | && \frac{T^2}{4\pi^2} = \frac{m}{D} &&|\cdot 4\pi^2 \\ | ||
| + | \Leftrightarrow | ||
| + | && T^2 = 4\pi^2 \,\frac{m}{D} &&|\sqrt{\quad}\\ | ||
| + | \Leftrightarrow | ||
| + | && T = 2 \pi \sqrt{\frac{m}{D}}\\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | '''e)''' Begründen Sie, dass die Frequenz nicht von der Amplitude der Schwingung abhängt. | ||
| + | :In der gefundenen Lösung der DGL hängt die Kreisfrequenz zwar von der Federhärte und der Masse ab, aber nicht von der Amplitude. | ||
| + | |||
| + | ====11) Eine "Schwingungswaage"==== | ||
| + | [[Datei:Waage_weltraum.jpg|thumb]] | ||
| + | *Erläutern Sie, warum man mit dieser Waage die Masse der Astronautin bestimmen kann. Benutzen Sie hierfür die Begriffe Trägheit und beschleunigende Kraft/Rückstellkraft. | ||
| + | |||
| + | Mit dieser Waage kann die Trägheit, also die träge Masse der Astronautin gemessen werden. Die beschleunigende Kraft (und damit die Impulsänderung) ist durch die Feder vorgegeben, verändert sich also nicht bei unterschiedlichen Massen. Bei einer größeren Masse wird sich daher die Geschwindigkeit weniger schnell verändern, was sich in einer niedrigeren Frequenz der Schwingung äußert. | ||
| + | |||
| + | *Wie verändert sich die Frequenz, wenn man die Amplitude der Schwingung verändert? Warum ist das für die Weltraumwaage sehr praktisch? | ||
| + | |||
| + | Die Frequenz einer Federschwingung hängt nicht von der Amplitude ab. Das ist praktisch, weil es für die Messung irrelevant ist, wie stark die Astronautin "angeschubst" wird. | ||
| + | |||
| + | Der leere Stuhl hat eine Masse von <math>m_0=2\, \rm kg</math> und schwingt mit einer Periode von <math>T=0{,}33\, \rm s</math>. | ||
| + | *Bestimmen Sie hieraus die Härte <math>D</math> der Feder. | ||
| + | |||
| + | Den Zusammenhang zwischen Winkelgeschwindigkeit, Federhärte und Masse kann man nach der Federhärte auflösen: | ||
| + | :<math> | ||
| + | \begin{array}{rcll} | ||
| + | \omega^2 &=& \frac{D}{m} & | \cdot m \\ | ||
| + | D &=& \omega^2\, m & | \ \omega =\frac{2\pi}{T}\\ | ||
| + | &=& \frac{4 \pi^2}{T^2} \, m\\ | ||
| + | &=& \frac{4 \pi^2}{(0{,}33\, \rm s)^2} \cdot 2\, \rm kg \\ | ||
| + | &=& 725 \frac{\rm N}{\rm m} & \left[ \rm { \frac{kg}{s^2}=\frac{kg\,m}{m\, s^2}=\frac{kg\,\frac{m}{s^2}}{m} = \frac{N}{m} } \right] | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Nun steigt die Astronautin in den Stuhl und die Periodendauer verlängert sich auf <math>T=1{,}87\, \rm s</math>. | ||
| + | *Welche Masse hat die Astronautin? | ||
| + | |||
| + | Diesmal löst man nach der Masse auf: | ||
| + | :<math> | ||
| + | \begin{array}{rcll} | ||
| + | \omega^2 &=& \frac{D}{m} & | \cdot m \ |\colon \omega^2\\ | ||
| + | m &=& \frac{D}{\omega^2}& | \ \omega =\frac{2\pi}{T}\\ | ||
| + | &=& \frac{D\, T^2}{4 \pi^2} \\ | ||
| + | &=& \frac{725 \frac{\rm N}{\rm m} \, (1{,}87\, \rm s)^2}{4 \pi^2} \\ | ||
| + | &=& 64{,}22\,\rm kg & \left[ \rm { \frac{N\,s^2}{m}= \frac{kg\,\frac{m}{s^2}\,s^2}{m}=kg} \right]\\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | Das ist die Masse von Astronautin und Stuhl, von der man noch die Stuhlmasse abziehen muss. Die Astronautin hat also eine Masse von <math>62{,}22\,\rm kg</math>. | ||
| + | |||
| + | Man kann die Masse der Astronautin auch ohne den Zwischenschritt über die Federhärte berechnen. An der Gleichung <math>m = \frac{D\, T^2}{4 \pi^2} </math> erkennt man, dass die Masse proportional zum Quadrat der Schwingungsdauer ist: | ||
| + | :<math> m \sim T^2 </math> | ||
| + | Das Verhältnis der Masse zum Quadrat der Schwingungsdauer ist daher immer gleich groß: | ||
| + | :<math> | ||
| + | \begin{array}{rcll} | ||
| + | \frac{m_{ges}}{{T_{ges}}^2 } &=& \frac{m_{Stuhl}}{{T_{Stuhl}}^2} & | \cdot {T_{ges}}^2 \quad \text{nach}\, m_{ges} \, \text{auflösen}\\ | ||
| + | m_{ges} &=& \frac{{T_{ges}}^2}{{T_{Stuhl}}^2} \, m_{Stuhl} \\ | ||
| + | &=& \frac{(1{,}87\, \rm s)^2}{(0{,}33\, \rm s)^2} \cdot 2\,\rm kg \\ | ||
| + | &=& 32{,}11 \cdot 2\,\rm kg \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | In einem Modellversuch schwingt ein Wagen zwischen zwei Federn. Die Federkonstante einer Feder beträgt <math>3\,\rm \frac{N}{m}</math>. Zusammen wirken sie wie eine Feder mit der doppelten Federkonstante. Der Wagen hat eine Masse von <math>190{,}6\,\rm g</math>. | ||
| + | |||
| + | *Wie schwer ist eine am Wagen befestigte Batterie, wenn der Wagen mit ihr nun in 5,6 Sekunden viermal schwingt? | ||
| + | |||
| + | Löst man die Formel für die Frequenz einer harmonischen Schwingung nach der Masse auf, so erhält man: | ||
| + | :<math>f = \frac{1}{2 \pi} \sqrt{\frac{D}{m}} \quad \Rightarrow \quad m= \frac{D}{4 \pi^2 \, f^2}</math> | ||
| + | |||
| + | Mit <math>f = \frac{4}{5,6 \rm \, s} = 0,714 \,\rm Hz</math> folgt: | ||
| + | |||
| + | :<math>m= \frac{2\cdot 3 \,\rm N/m}{4 \pi^2 \, (0,714 \,\rm 1/s)^2} = 0,298\, \rm kg</math> | ||
| + | Das ist die Masse des Wagens und der Batterie zusammen. Die Batterie hat also eine Masse von <math>298\, \rm g - 190,6 \, \rm g \approx 107 g</math>! | ||
| + | |||
| + | ====12) Schaukeltier II==== | ||
| + | Große Kinder haben eine größere Masse, wodurch sie "langsamer", also mit einer geringeren Frequenz, schwingen! | ||
| + | |||
| + | ====13) Schwingmännchen III==== | ||
| + | Das Männchen bringt 200g auf die Waage und verlängert beim Dranhängen die vorher unbelastete Feder um 40cm. | ||
| + | |||
| + | *Wieso beträgt die Federkonstante (D) gerade 1/20 N/cm = 0,05 N/cm? | ||
| + | :Die Gewichtskraft von 200g beträgt ca. 2 Newton: | ||
| + | :<math>F_G = m \, g = 0{,}200\,\rm kg \cdot 9,81 \frac{\rm N}{\rm kg} \approx 2\,\rm N</math> | ||
| + | |||
| + | Die Federkonstante gibt die benötigte Kraft pro Verlängerung an: | ||
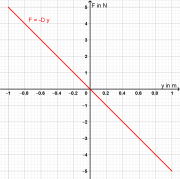
| + | :<math>D=\frac{\rm Kraft}{\rm Verl\ddot a ngerung}=\frac{2\, \rm N}{40 \,\rm cm}=0{,}05\frac{\rm N}{\rm cm} =5\frac{\rm N}{\rm m} </math> | ||
| + | :[[Datei:Aufgabe Schwingmännchen III Lösung F-y-Diagramm.png|thumb|none]] | ||
| + | |||
| + | *Mit welcher Frequenz wird das Männchen schwingen? | ||
| + | :Mit <math>\omega ^2 = \frac{D}{m}</math> folgt: | ||
| + | ::<math>f = \frac{1}{2 \, \pi}\sqrt{\frac{D}{m}}= \frac{1}{2 \, \pi} \sqrt{\frac{5\,\rm N/m}{0{,}2\,\rm kg}}\approx 0{,}80 \,\rm Hz </math> | ||
| + | |||
| + | :Es schwingt etwas weniger als einmal pro Sekunde. | ||
| + | |||
| + | *Muss man ergänzen oder bei Aufgaen entfernen, da es sich mit A14 überschneidet (An Inhaber der Website) | ||
| + | |||
| + | ====14) Schwingmännchen IV==== | ||
| + | Um die Frequenz zu verdoppeln, muss man die Federhärte vervierfachen, also ein Viertel der Feder benutzen, oder die Masse vierteln. | ||
| + | |||
| + | ====15) Schwingmännchen V==== | ||
| + | {| | ||
| + | |Es gilt: | ||
| + | |<math>\omega = 2\ \Pi \ f=\sqrt{\frac{D}{m}}</math> | ||
| + | |<math>E=\frac{1}{2}\, m \ (\omega \hat y)^2 = \frac{1}{2}D\ \hat y^2</math> | ||
| + | |- | ||
| + | |*die Federkonstante verdoppelt: | ||
| + | |Die Frequenz erhöht sich um den Faktor <math>\sqrt{2}</math>. | ||
| + | |Der Energiegehalt verdoppelt sich. | ||
| + | |- | ||
| + | |*die Masse verdoppelt: | ||
| + | |Die Frequenz verringert sich um den Faktor <math>\sqrt{2}</math>. | ||
| + | |Der Energiegehalt bleibt gleich! (Das Männchen ist zwar schwerer, schwingt aber dafür langsamer.) | ||
| + | |- | ||
| + | |*die Amplitude verdoppelt: | ||
| + | |Die Frequenz bleibt gleich! | ||
| + | |Der Energiegehalt vervierfacht sich. | ||
| + | |} | ||
| + | |||
| + | ====16) Schaukeltier III==== | ||
| + | Beim Anschubsen müssen die Kinder im richtigen Rythmus, nämlich in der Eigenfrequenz anregen, sonst nimmt die Schwingung die Energie nicht an und der Effekt ist gering! Zu schnelles Anschubsen bringt also nichts. | ||
| + | |||
| + | ====17) Schwingungskategorien==== | ||
| + | Da finden sich im Kapitel [[Energiezufuhr_bei_Schwingungen#Übersicht|Energiezufuhr bei Schwingungen]] Beispiele. | ||
| + | |||
| + | ====18) Wackelnder Rückspiegel==== | ||
| + | *Ich kann die Anregungsfrequenz verändern, also langsamer oder schneller fahren. | ||
| + | *Ich kann die Eigenfrequenz des Spiegels ändern, indem ich z.B. seine Masse vergrößere. (Das könnte man mit Knete oder einer Wäschklammer erreichen, dann verringert sich die Eigenfrequenz.) | ||
| + | *Ich kann den Spiegel dämpfen und ihm die Energie entziehen, z.B. indem ich mit dem Finger dranfasse. (Das ist die einzige Lösung, die dauerhaft bei allen Geschwindigkeiten funktioniert.) | ||
| + | |||
| + | ====19) harmonische Schwingung==== | ||
| + | Das kann man im Kapitel [[Woran man eine harmonische Schwingung erkennt (Vier gleichwertige Kriterien)|Woran man eine harmonische Schwingung erkennt]] lesen. | ||
| + | |||
| + | ====20) Energie==== | ||
Geg:<math>m = 1kg</math> | Geg:<math>m = 1kg</math> | ||
:<math>T = 1s</math> | :<math>T = 1s</math> | ||
| Zeile 48: | Zeile 376: | ||
Rechnung: | Rechnung: | ||
| + | Entweder man setzt in die fertige Formel ein: | ||
| + | :<math>E_{kin}=\frac{1}{2}\, m\,(\hat y\, \omega)^2 = E_{kin}=\frac{1}{2}\, m\,(\hat y\, 2\pi\, f)^2</math> | ||
| − | + | Oder man überlegt es sich noch einmal selbst: | |
| − | :<math>E_{kin}= | + | Die maximale Bewegungsenergie ist auch die Gesamtenergie der Schwingung: |
| + | :<math>E_{kin}=\frac{1}{2}\, m\,\hat v^2</math> | ||
| + | |||
| + | Die maximale Geschwindigkeit beträgt: | ||
| + | :<math>\hat v = \hat y \, \omega = \hat y \, 2\pi f = 0{,}01\, \rm m \cdot 2\pi \cdot 1\,\rm Hz = 0{,}0628\,\rm m/s</math> | ||
| + | |||
| + | Jetzt noch einsetzen: | ||
| + | :<math>E_{kin}=\frac{1}{2}\cdot 1\,\rm kg \cdot \hat (0{,}0628\,\rm m/s)^2 \approx 0{,}002\,\rm J </math> | ||
Das ist sehr wenig! | Das ist sehr wenig! | ||
| − | ====Energie II==== | + | ====22) Energie II==== |
Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat? | Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat? | ||
| Zeile 75: | Zeile 412: | ||
Für eine Amplitude von nur 1cm = 0,01 m benötigt man schon eine Frequenz von ca 23 Hz. | Für eine Amplitude von nur 1cm = 0,01 m benötigt man schon eine Frequenz von ca 23 Hz. | ||
| − | ====Energie III==== | + | ====23) Energie III==== |
Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen. | Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen. | ||
| Zeile 82: | Zeile 419: | ||
Die Energie ist also proportional zum Quadrat der Frequenz. Bei einer Verdoppelung wird sich der Energiegehalt vervierfachen! | Die Energie ist also proportional zum Quadrat der Frequenz. Bei einer Verdoppelung wird sich der Energiegehalt vervierfachen! | ||
| − | ====1 Schwebung==== | + | ====24) Zwei schwingende Wagen==== |
| + | [[Datei:Schwingende_Wagen.jpg|thumb|Die Wagen stehen auf einer Schiene und sind mit einer Feder verbunden.]] | ||
| + | Wenn die Wagen schwingen haben sie zu unterschiedlichen Phasen der Schwingung unterschiedlich viel Impuls. Der Impuls nach rechts soll als positiv gewertet werden. | ||
| + | |||
| + | Ebenso ändert sich die Energiemenge in der Feder und in den Wagen. | ||
| + | |||
| + | *Ergänze in der Tabelle qualitativ die Angaben von Impuls und Energie. | ||
| + | <br style="clear: both" /> | ||
| + | |||
| + | {|class="wikitable" | ||
| + | !Phase | ||
| + | !Bild | ||
| + | !colspan="2"|Impuls | ||
| + | !colspan="2"|Energie | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | |width="100px"|links | ||
| + | |width="100px"|rechts | ||
| + | |width="100px"|Feder | ||
| + | |width="100px"|Kugeln | ||
| + | |- | ||
| + | |<math>t=0\,\rm s</math> <br> Ruhelage | ||
| + | |[[Datei:Schwingung zwei Körper Ruhelage.png|497px]] | ||
| + | | maximaler Impuls (positiv) | ||
| + | | minimaler Impuls (negativ) | ||
| + | | keine Spannenergie | ||
| + | | maximale kinetische Energie | ||
| + | |- | ||
| + | |<math>t=\frac{1}{4} \, T </math> <br> innere Umkehrpunkte | ||
| + | |[[Datei:Schwingung zwei Körper Umkehrpunkt innen.png|497px]] | ||
| + | | kein Impuls | ||
| + | | kein Impuls | ||
| + | | maximale Spannenergie | ||
| + | | keine kinetische Energie | ||
| + | |- | ||
| + | |<math>t=\frac{1}{2}\, T \,\rm s</math> <br> Ruhelage | ||
| + | |[[Datei:Schwingung zwei Körper Ruhelage.png|497px]] | ||
| + | | minimaler Impuls (negativ) | ||
| + | | maximaler Impuls (positiv) | ||
| + | | keine Spannenergie | ||
| + | | maximale kinetische Energie | ||
| + | |- | ||
| + | |<math>t=\frac{3}{4}\, T </math> <br> äußere Umkehrpunkte | ||
| + | |[[Datei:Schwingung zwei Körper Umkehrpunkt aussen.png|497px]] | ||
| + | | kein Impuls | ||
| + | | kein Impuls | ||
| + | | maximale Spannenergie | ||
| + | | keine kinetische Energie | ||
| + | |- | ||
| + | |<math>t=T </math> <br> Ruhelage | ||
| + | |[[Datei:Schwingung zwei Körper Ruhelage.png|497px]] | ||
| + | | maximaler Impuls (positiv) | ||
| + | | minimaler Impuls (negativ) | ||
| + | | keine Spannenergie | ||
| + | | maximale kinetische Energie | ||
| + | |} | ||
| + | |||
| + | ====25) Wasserstoffmolekül==== | ||
| + | Ein H<sub>2</sub>-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. | ||
| + | Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 10<sup>11</sup> Hz. | ||
| + | |||
| + | *Bestimmen sie die "Federkonstante" der gedachten Feder zwischen den Molekülen. | ||
| + | |||
| + | Wie die Moleküle im Modell schwingen, kann man [[Energie und Impuls einer mechanischen Schwingung#Animation|hier]] sehen. Wichtig ist, dass beide Atome mit der gleichen Frequenz schwingen. | ||
| + | |||
| + | Die Situation ist symmetrisch und man betrachtet für die Rechnung die Hälfte des Versuchsaufbaus. Durch die Halbierung der Feder verdoppelt sich dann die berechnete Federkonstante. | ||
| + | |||
| + | Die Masse eines H-Atoms beträgt ca. <math>1{,}66 \cdot 10^{-27}\,\mathrm{kg}</math>. | ||
| + | |||
| + | Zwischen Kreisfrequenz, Federkonstante und Masse besteht der Zusammenhang: | ||
| + | <math>\omega^2 = \frac{D}{m} \quad \Rightarrow \quad D = \omega^2 \, m = 4 \pi^2 \, f^2 \, m </math> | ||
| + | :<math>D = 4 \pi^2 \, (9{,}2\cdot10^{11}\,\rm Hz)^2 \cdot 1{,}66 \cdot 10^{-27}\,\mathrm{kg}= 0,055 \frac{\rm N}{\rm m}</math> | ||
| + | Die gesamte Feder hätte somit eine Federkonstante von <math>0,028 \frac{\rm N}{\rm m}</math>. Makroskopisch wäre das eine sehr schwache Feder. Für das "kleine" Wasserstoffatom ist das aber eine sehr starke Kopplung. | ||
| + | |||
| + | *Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10<sup>-10</sup>m schwingen? | ||
| + | Die Energie einer Hälfte ergibt sich zu: | ||
| + | :<math>E = \frac{1}{2}\, m \, \hat y^2 \, \omega^2 = \frac{1}{2}\, 1{,}66 \cdot 10^{-27}\,\mathrm{kg} \, ( 10^{-10}\,\rm m)^2 \, (2 \pi \, 9{,}2\cdot10^{11}\,\rm Hz)^2 = 2{,}8\cdot 10^{-22}\,\rm J</math> | ||
| + | :<math>E_{ges}=5{,}6 \cdot 10^{-22}\,\rm J</math> | ||
| + | Makroskopisch nicht viel, aber bei einem Mol, also <math>6{,}022 \cdot 10^{23}</math> Molekülen, immerhin ca. <math>340 \, \rm J</math>! | ||
| + | |||
| + | ====26) Molekül-Spektroskopie==== | ||
| + | *Bei großen oder langen Molekülen findet man viele Frequenzen, bei denen die Energie nicht auf der anderen Seite ankommt. Bei einem Molekül wie Kohlenmonoxid (CO) nur eine. Wie kann man das erklären? | ||
| + | [[Datei:CO-Molekül.png|thumb|200px|Das CO-Molekül als einfaches Modell.]] | ||
| + | :Das CO-Molekül hat nur eine Eigenschwingung mit einer Eigenfrequenz. Dabei schwingen die Atome aufeinander zu und wieder weg. Größere Moleküle verhalten sich wie ausgedehnte Körper, etwa eine Stange oder eine Platte. Deswegen haben sie viele Eigenschwingungen und viele Eigenfrequenzen. | ||
| + | :Wird die Energie in der "passenden" Frequenz zugeführt, so nimmt das Molekül viel Energie auf und gibt sie dann wieder ab. Dabei wird die Energie aber nicht mehr in der ursprünglichen Richtung weitergeleitet und auch die Frequenz kann sich ändern. | ||
| + | |||
| + | *Bei Kohlenmonoxid misst man eine Absorption bei der Frequenz <math>f=6{,}5\cdot 10^{13}\,\rm Hz</math>. Als Modell für das Molekül kann man vereinfachend zwei punktförmige Massen annehmen, die mit einer masselosen Feder verbunden sind. (So wie [[Energie_und_Impuls_einer_mechanischen_Schwingung#Animation|hier]].) | ||
| + | :Bestimmen Sie die "Federkonstante" des Moleküls. | ||
| + | |||
| + | Die Massen der Atome betragen in etwa: <math>m_C = 12\,\rm u</math> und <math>m_O = 16\, \rm u</math>, mit <math>u=1{,}66\cdot 10^{-27}\,\rm kg</math>. | ||
| + | |||
| + | Beide Atome schwingen mit der gleichen Frequenz. Der Schwerpunkt liegt dabei näher am massereicheren O-Atom und bleibt erhalten. | ||
| + | Das Verhältnis der Abstände zwischen Atom und Schwerpunkt beträgt 16 zu 12 oder 4 zu 3. | ||
| + | Nun kann man entweder die Schwingung des C-Atoms betrachten und die Federkonstante diesen Teils der Feder berechnen oder eben den Teil des O-Atoms. Für das Sauerstoffatom gilt: | ||
| + | :<math>\omega^2=\frac{D_O}{m} \quad \Rightarrow \quad D = \omega^2 \, m = 4\pi^2\, (6{,}5\cdot 10^{13}\,\rm Hz)^2 \cdot 16\cdot 1{,}66\cdot 10^{-27}\,\rm kg = 4430 \frac{\rm N}{\rm m}</math> | ||
| + | :Dies ist die Federhärte von <math>3/7</math> der Feder. Die ganze Feder ist um den Faktor <math>7/3</math> länger und somit weniger hart, die Federhärte der gesamten Feder beträgt: | ||
| + | :<math>D= 4430 \frac{\rm N}{\rm m}: \frac{7}{3} = 1900 \frac{\rm N}{\rm m}</math> | ||
| + | |||
| + | Genauere Informationen findet man im Artikel "[http://de.wikipedia.org/wiki/Infrarotspektroskopie Infrarotspektroskopie]" bei Wikipedia oder Interessantes zum Verhalten von CO_2 beim Treibhauseffekt in diesem Artikel der Chemiedidaktik Bayreuth zu [http://daten.didaktikchemie.uni-bayreuth.de/umat/inhaltsv.htm Grundlagen der IR-Spektroskopie] (nicht mehr online??). | ||
| + | |||
| + | ====27) Schwebung von Stimmgabeln==== | ||
| + | Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz, die andere hat eine Frequenz von 438 Hz. | ||
| + | <br>Was kann man hören? | ||
| + | :Man hört eine Schwebung mit einer Frequenz von 2Hz. Also einen Ton, der zweimal pro Sekunde laut und zweimal pro Sekunde leise ist. | ||
| + | |||
| + | ====28) Schwebung==== | ||
Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz. Schätzen Sie die Frequenz der anderen Stimmgabel ab. | Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz. Schätzen Sie die Frequenz der anderen Stimmgabel ab. | ||
'''Lösung:''' | '''Lösung:''' | ||
| − | <br/> Das Schätzen der Frequenz der anderen Stimmgabel wäre | + | <br/> Das Schätzen der Frequenz der anderen Stimmgabel wäre äußerst schwierig, da die Frequenz wohl viel zu hoch wäre. Man kann aber die Frequenz der Schwebung abschätzen. In unserem Beispiel ergab dies etwa <math>1{,}2\,\rm Hz</math>. Da die Frequenz der zweiten Stimmgabel geringer sein wird, als die der anderen (der Reiter verlangsamt die Schwingung, indem er zusätzliche Masse einbringt) und die Frequenz der Schwebung gerade die Differenz der Frequenzen der beiden Stimmgabeln ist, ergibt sich: |
| − | <br/><math> | + | <br/><math>\rm 440\,\rm Hz - x\,\rm Hz=1{,}2\,\rm Hz \Rightarrow x=438{,}8</math> |
| − | + | ||
| − | ==== | + | Die zweite Stimmgabel hat also etwa die Frequenz <math>438{,}8\,\rm Hz</math>. |
| + | |||
| + | ====29) Überlagerung==== | ||
Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y<sub>1</sub> und y<sub>2</sub> entsteht mit Hilfe des Zeigerdiagramms: | Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y<sub>1</sub> und y<sub>2</sub> entsteht mit Hilfe des Zeigerdiagramms: | ||
| − | [[Bild:Schwingung_Überlagerung_Aufgabe_1.png| | + | [[Bild:Schwingung_Überlagerung_Aufgabe_1.png|thumb|470px|none|<math>y_1 = 2\,\rm cm \, \sin(2\,t)\qquad y_2 = 4\,\rm cm \, \sin(2\,t+\pi) \qquad y = 2\,\rm cm\, \sin(2\,t+\pi)</math>]] |
| + | |||
| + | Beide Schwingungen haben die selbe Winkelgeschwindigkeit (<math>\omega = 2\,\rm Hz</math>). | ||
| + | Die zweite Schwingung ist um <math>\pi</math> phasenverschoben, also genau gegenphasig. | ||
| + | |||
| + | Da die Schwingungen gegenphasig sind, eliminieren sie sich gegenseitig, da die zweite Schwingung aber die doppelte Amplitude der ersten Schwingung hat, wird ein Ton mit der halben Amplitude der zweiten Schwingung, aber ohne Phasenverschiebung zu dieser hörbar sein. | ||
| + | |||
| + | [[Bild:Schwingung_Überlagerung_Aufgabe_2.png|thumb|470px|none|<math>y_1 = 2\,\rm cm \, \sin(2\,t)\qquad y_2 = 4\,\rm cm \, \sin(2\,t+\pi/2) \qquad y=4{,}47\,\rm cm \cdot \sin(2\, t + 1{,}11)</math>]] | ||
| + | Die neue Amplitude, also die Zeigerlänge des Summenvektors, kann man mit dem Satz des Pythagoras berechnen: | ||
| + | :<math>\hat y = \sqrt{(2\,\rm cm)^2+(4\,\rm cm)^2} \approx 4{,}47\,\rm cm</math> | ||
| + | Die Phasenverschiebung <math>\alpha</math> zur Schwingung Nr.1 (roter Zeiger) ergibt sich aus dem Tangens im rechtwinkligen Dreieck: | ||
| + | :<math>\tan(\alpha)= 4\,\rm cm / 2\,\rm cm = 2 \quad \Rightarrow \quad \alpha = \arctan(2)\approx 1{,}11 \quad (\hat = 63{,}4^\circ)</math> | ||
| + | Also hat die Überlagerung der Schwingungen die Schwingungsgleichung: | ||
| + | :<math>y=4{,}47\,\rm cm \cdot \sin(2\, t + 1{,}11)</math> | ||
| − | + | [[Bild:Schwingung_Überlagerung_Aufgabe_3.png|thumb|470px|none|<math>y_1 = 2\,\rm cm \, \sin(2\,t)\qquad y_2 = 2\,\rm cm\, \sin(2\,t+\pi) \quad y=0\,\rm m</math>]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Bild: | + | |
| − | + | ||
| − | + | Da die Zeiger entgegengesetzt gleich sind, heben sich die beiden Schwingungen gerade auf. | |
| − | + | ||
| − | + | ||
| + | ==Schwieriges und Anderes== | ||
====7 Schwingung bei bekannter Energie==== | ====7 Schwingung bei bekannter Energie==== | ||
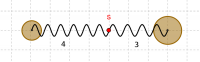
Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. | Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. | ||
Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird? | Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird? | ||
| − | + | Gegeben: | |
| + | <math>m =0{,}6\,\rm kg \qquad D=100\,\frac{\rm N}{\rm m} \qquad E=1\,\rm J </math> | ||
| − | Die Charakteristik einer | + | Die Charakteristik einer Schwingung definieren wir als Angabe von der Frequenz <math>f</math> und der Amplitude <math>\hat y</math>. |
| − | <br/>Es wird mit der doppelten Federstärke <math>D</math> gerechnet, da wir | + | <br/>Es wird mit der doppelten Federstärke <math>D</math> gerechnet, da wir den Fall auf nur einen Wagen idealisieren (Stille Annahme: Symmetrie der Bewegung). |
<br/>Zunächst widmen wir uns der Frequenz <math>f</math>: | <br/>Zunächst widmen wir uns der Frequenz <math>f</math>: | ||
| − | + | :<math>f=</math><math>{\omega}\over 2\pi</math><math>=</math><math>\sqrt {2D \over m}\over 2\pi</math><math>=</math><math>\sqrt {{200 {N\over m}} \over 0.6kg}\over 2\pi</math><math>=</math><math>2.91Hz</math> | |
Nun zur Amplitude <math>\hat y</math>: | Nun zur Amplitude <math>\hat y</math>: | ||
| − | + | :<math>E_{pot}=</math><math>2\left({2D\over 2}{\hat y}^2\right)</math> | |
| − | + | :<math>\hat y=</math><math>\sqrt {E\over 2D}</math><math>=</math><math>\sqrt {1Jm\over {200N}}</math><math>=</math><math>{0.1\over{\sqrt 2}}m</math><math>=</math><math>0.07m</math> | |
| − | + | (für einen einzelnen Wagen; das Gesamtsystem hat jedoch 2<math>\hat y</math>) | |
| − | + | ||
| − | + | ||
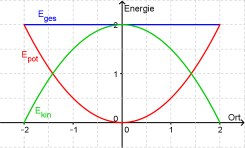
| − | + | ====9 E<sub>kin</sub> = E<sub>Spann</sub>==== | |
| − | + | [[Bild:Schwingung_E_vom_Ort_Federschwingung.png|thumb|right|245px|Die Energieformen eines (horizontalen) Federpendels in Abhängigkeit vom Ort.]] | |
| − | + | Es wird gefragt für welche Auslenkung die Energie gleichermaßen in dem Impuls als auch in der Feder ist. Also wann die kinetische Energie gerade gleich der kinetischen bzw. der Spannenergie ist. | |
| − | + | Bei der gleichmäßigen Verteilung der Energie auf die Bewegung und die Feder, enthält sowohl die Feder als auch die Bewegung gerade die Hälfte der Energie: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | :<math>E_{pot}= \frac{1}{2}\, E_{ges}</math> | |
| − | + | :<math>\frac{1}{2} \, D\, y^2 = \frac{1}{2}\,\frac{1}{2} D \, \hat y^2</math> | |
| − | :<math>E_{ | + | :nach y aufgelöst: |
| − | + | :<math>y=\frac{1}{\sqrt{2}} \, \hat y \approx 0,7 \, \hat y</math> | |
| − | :<math> | + | Bei ca. 70% der Amplitude ist die Energie gleichmäßig auf Bewegung und Feder verteilt. |
| − | :nach | + | |
| − | :<math> | + | |
====10 Zeitlicher Mittelwert von E<sub>kin</sub> und E<sub>Spann</sub>==== | ====10 Zeitlicher Mittelwert von E<sub>kin</sub> und E<sub>Spann</sub>==== | ||
Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel. | Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel. | ||
Aktuelle Version vom 12. November 2025, 21:36 Uhr
(Kursstufe > Mechanische Schwingungen)
Inhaltsverzeichnis
- 1 1) Energieformen
- 2 2) Schaukeltier
- 3 3) Zeigermodell
- 4 4) Uhrzeiger
- 5 5) Schwingmännchen
- 6 6) Stimmgabel
- 7 7) Horizontales Federpendel
- 8 8) Schwingmännchen II
- 9 9) Messungen an einem Federpendel
- 10 10) DGL
- 11 11) Eine "Schwingungswaage"
- 12 12) Schaukeltier II
- 13 13) Schwingmännchen III
- 14 14) Schwingmännchen IV
- 15 15) Schwingmännchen V
- 16 16) Schaukeltier III
- 17 17) Schwingungskategorien
- 18 18) Wackelnder Rückspiegel
- 19 19) harmonische Schwingung
- 20 20) Energie
- 21 22) Energie II
- 22 23) Energie III
- 23 24) Zwei schwingende Wagen
- 24 25) Wasserstoffmolekül
- 25 26) Molekül-Spektroskopie
- 26 27) Schwebung von Stimmgabeln
- 27 28) Schwebung
- 28 29) Überlagerung
- 29 Schwieriges und Anderes
1) Energieformen
Beispiele sind im Abschnitt "Grundbegriffe von Schwingungen" zu finden.
2) Schaukeltier
Das kann man im Abschnitt "Begriffe einer mechanischen Schwingung" nachlesen.
3) Zeigermodell
Der Versuch ist im Wiki unter im Kapitel Zeigerdarstellung beschrieben, oder im Heft.
4) Uhrzeiger
- Die Winkelgeschwindigkeit gibt an welcher Winkel in welcher Zeit überstrichen wird. Beim Sekundenzeiger eben 360° oder [math]2 \,\pi[/math] in einer Minute.
- Die Periodendauer beträgt 60s und die Frequenz 1/60 Hz.
- Die Winkelgeschwindigkeit entspricht der Geschwindigkeit der Zeigerspitze bei einem Radius von 1.
- Verzehnfacht man den Radius, so verzehnfacht sich auch die Geschwindigkeit: [math]v=\omega \, r = \frac{2\,\pi}{60\,s}\cdot 10\,\rm cm = 1{,}05 \frac{cm}{s}[/math]
5) Schwingmännchen
- Der Zeiger hat eine Länge von 3cm.
6) Stimmgabel
- [math]T=\frac{1}{f}=\frac{1}{440\, \rm 1/s} = 0{,}00227\, \rm s[/math]
- [math]\omega = 2\,\pi\,f = 2760\, \rm Hz[/math]
- [math]y(t)=2 \,\rm mm \cdot \sin (2760\,\rm Hz \cdot t)[/math]
- [math]v(t)=5520 \,\rm mm/s \cdot \cos (2760\,\rm Hz \cdot t) = 5{,}52 \,\rm m/s \cdot \cos (2760\,\rm Hz \cdot t) [/math]
- [math]a(t)=-15200 \,\rm m/s^2 \cdot \sin (2760\,\rm Hz \cdot t)[/math]
- Maximale Geschwindigkeit: [math]\hat v = 5{,}52 \,\rm m/s \approx 20 \, \rm km/h[/math]
- Maximale Beschleunigung: [math]\hat a = 15200 \,\rm m/s^2[/math] (Das ist das 1500-fache der Erdbeschleunigung!)
7) Horizontales Federpendel
- Die maximale Auslenkung (und die maximale Geschwindigkeit) des Wagens bleibt konstant, daher geht keine Energie aus der Schwingung heraus.
- Zu Beginn (t=0s) befindet sich der Wagen in der Ruhelage (y=0m) und wird mit 1m/s nach rechts angeschubst.
- Der Wagen bleibt in den äußeren Umkehrpunkten stehen und ist beim Durchgang durch die Ruhelage besonders schnell. Bleibt der Wagen z.B. im linken Umkehrpunkt stehen, so wirkt auf ihn eine Kraft nach rechts, die Geschwindigkeit nach rechts nimmt zu. Bis zur Ruhelage wird der Wagen weiter beschleunigt, danach wird er wieder abgebremst, weil die Rückstellkraft nun nach links wirkt.
- Die Auslenkung des Wagens hinkt der Geschwindigkeit des Wagens dabei um eine Viertel Schwingung hinterher:
t=0 v maximal, positiv y=0 t=1/4 T v=0 y maximal, positiv t=1/2 T v maximal, negativ y=0 t=3/4 T v=0 y maximal, negativ t=T v maximal, negativ y=0
- Die Beschleunigung hat die gleiche Richtung wie die Kraft. Da für die Rückstellkraft [math]F = -D\, y[/math] gilt, ist auch die Beschleunigung immer entgegengesetzt zur Auslenkung.
- Aus dem Graphen der Auslenkung y kann man die Periodendauer von drei Sekunden ablesen: [math]T = 3 \, \rm s[/math]. Also folgt für die Winkelgeschwindigkeit:
- [math]\omega = 2\pi \, f = \frac{2\pi}{T}\approx 2\,\rm Hz[/math]
Aus der Winkelgeschwindigkeit und der Amplitude kann man nun die maximale Geschwindigkeit und Beschleunigung berechnen:
- [math]\hat v = \hat y\, \omega = 0{,}5\,\rm m \cdot 2\, \rm Hz = 1\, \rm m/s[/math]
- [math]\hat a = \hat y\, \omega^2 = 0{,}5\,\rm m \cdot (2\, \rm Hz)^2 = 2\, \rm m/s^2[/math]
- Die so berechneten Werte stimmen mit den an den Graphen ablesbaren Werten gut überein. Die maximale Beschleunigung ist dort etwas größer als 2m/s2, wahrscheinlich ist die Periodendauer etwas kleiner als die abgelesenen drei Sekunden.
- Auch an den Steigungen der Graphen kann man das Ergebnis kontrollieren: Die maximale Steigung des Graphen der Auslenkung beträgt tatsächlich gerade 1m/s, die maximale Steigung des Graphen der Geschwindigkeit ist tatsächlich 2m/s2.
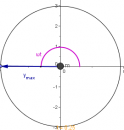
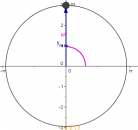
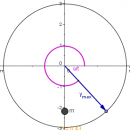
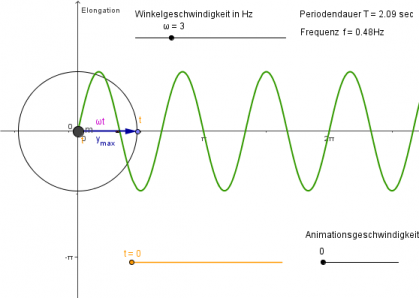
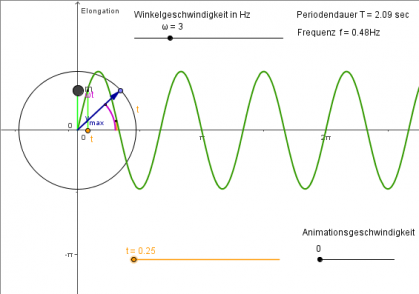
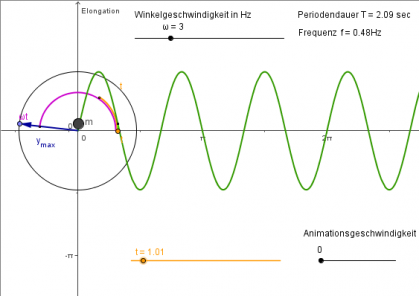
8) Schwingmännchen II
- Wie groß sind Amplitude, Frequenz und Periodendauer?
- [math]\hat y = 5\,\rm cm[/math]
- [math]2 \, \Pi \ f = 3 \,\rm Hz \Rightarrow f \approx 0{,}48 \,\rm Hz[/math]
- [math]T=\frac{1}{f}\approx 2{,}1 \,\rm s[/math]
- Zeichnen Sie das Ortsdiagramm, das Geschwindigkeitsdiagramm und das Beschleunigungsdiagramm jeweils in ein Koordinatensystem.
Die Geschwindigkeit und die Beschleunigung ergeben sich als erste und zweite Ableitung der Auslenkung:
- [math]v(t)=\dot y(t)=5 \, \rm cm \ 3 \,\rm Hz \cos(3\, \rm Hz \ t) = 15 \,\rm cm/s \cos(3 \,\rm Hz \ t)[/math]
- [math]a(t)=\dot v(t)= -15 \,\rm cm/s\cdot 3\,\rm Hz \sin(3 \,\rm Hz \ t) = \dot v(t)= -45 \,\rm cm/s^2 \sin(3 \,\rm Hz \ t)[/math]
Das kann man nun zeichnen.
- Zeichen Sie zum Ortsdiagramm die Zeiger für die Zeitpunkte t=0s, t=0,25s und t=1s.
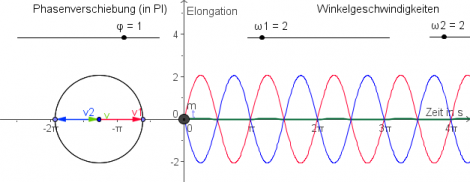
Der Zeiger hat am Anfang ([math]t = 0 \,\rm s[/math]) den Drehwinkel [math]\alpha = 0[/math]. Danach gilt : [math]\alpha = \omega \, t[/math]
Für [math]t = 0{,}25 \,\rm s\: \qquad \alpha = 3\,\rm Hz \cdot 0{,}25\,\rm s= 0{,}75 = 0{,}75 \cdot \frac{180^\circ}{\pi}= 43^\circ[/math]
- Wo ist das Männchen nach 1,6 Sekunden und wie schnell ist es?
- [math]y(1{,}6 \,\rm s) = 5 \,\rm cm \sin(3 \,\rm Hz 1{,}6 \,\rm s) \approx 5 \,\rm cm \ (-1) = -5 \,\rm cm[/math]
- Das Männchen ist fast am unteren Umkehrpunkt!
- [math]v(t)=\dot y(t)=5 \,\rm cm \ 3 \,\rm Hz \cos(3 \,\rm Hz \ t) = 15 \,\rm cm/s \cos(3 \,\rm Hz \ t)[/math]
- [math]v(1{,}6 \,\rm s)=15 \,\rm cm/s \cos(3 \,\rm Hz \ 1{,}6 \,\rm s) \approx 15 \,\rm cm/s \cdot 0{,}1 = 1{,}5 \,\rm cm/s [/math]
- Dort bleibt es annähernd stehen.
- Wie schnell ist das Männchen maximal?
- [math]\hat v = 15 \,\rm cm/s [/math]
9) Messungen an einem Federpendel
An eine Feder wird ein Gewichtsstück gehängt und zum Schwingen gebracht. In einem Experiment soll untersucht werden wovon die Periodendauer dieses Federpendels abhängt.
- a) Nennen Sie mögliche Größen, von denen die Periodendauer abhängen könnte.
- Die Periodendauer könnte von allen möglichen Faktoren abhängen: Masse des Gewichtsstücks, Härte der Feder, maximale Auslenkung der Schwingung, Erdbeschleunigung, Breite des Gewichtsstücks, Luftdruck, Lufttemperatur, Masse der Feder, Material der Feder, Uhrzeit, Mondphase, Sonnenaktivität, ...
- b) Beschreiben Sie wie man die Messungen durchführen muss, damit man diese Abhängigkeiten untersuchen kann.
- Man muss eine der Größen variieren und alle anderen Einflussfaktoren dabei konstant halten.
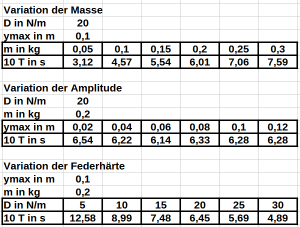
- c) Die folgenden Tabellen zeigen die Messergebnisse von drei Versuchsreihen. Bestimmen Sie zunächst rechnerisch von welchen Größen die Periodendauer abhängt und von welchen nicht. Berechnen Sie dann eine Formel für die Periodendauer in Abhängigkeit von den entsprechenden Größen.
- d) Zeigen Sie durch eine Rechnung, dass für das Federpendel der Zusammenhang [math]\omega^2 = \frac{D}{m}[/math] gilt.
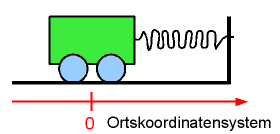
10) DGL
Ein Wagen ist mit einer Feder an einem Tisch befestigt. (Siehe Abbildung)
Für diese Situation hat man folgende Differentialgleichung aufgestellt:
- [math]0{,}1\,{\rm kg}\,\cdot \ddot y(t) = -0{,}4\,{\rm\tfrac{N}{m}} \cdot y(t)[/math]
a) Erläutern Sie die Gleichung.
- Die Variable y(t) beschreibt den Ort des Wagens im Koordinatensystem in Abhängigkeit von der Zeit, also das Ort-Zeit-Gesetz der Bewegung des Wagens.
- Die rechte Seite der Gleichung gibt an welche Kraft auf den Wagen im Ort y wirkt. Die Feder ist am Ort y=0m entspannt, dort wirkt keine Kraft. Wird die Feder um die Strecke y zusammengedrückt oder verlängert, so wirkt eine zur Längenveränderung proportionale Kraft. Die Feder erfüllt offensichtlich das Hooksche Gesetz mit der Federhärte 0,4 Newton pro Meter. Das Minuszeichen gibt an, dass bei einem Ort rechts vom Ursprung die Kraft nach links wirkt und umgekehrt.
- Die linke Seite der Gleichung beschreibt welche Beschleunigung aus der wirkenden Kraft resultiert. Denn es gilt: [math]F=m\,a[/math], wobei die Beschleunigung a die zweite zeitliche Ableitung des Ortes y ist.
- Alle Lösungen [math]y(t)[/math] der DGL beschreiben Bewegungen, die von diesem physikalischen System ausgeführt werden können. Ein Ortsgesetz [math]y(t)[/math], welches keine Lösung der DGL ist, beschreibt eine Bewegung, die der Wagen nicht ausführen kann.
b) Untersuchen Sie welche der nachfolgenden Funktionen eine Lösung der DGL ist:
- Zuerst berechnet man die zweite zeitliche Ableitung der Ortsfunktion. Die Änderung von Metern ist Meter pro Sekunde und deren Änderung ist Meter pro Sekunde im Quadrat:
- [math]y_1(t)=0\,{\rm m} \quad \Rightarrow \quad \ddot y_1(t) = 0\,{\rm\tfrac{m}{s^2}}[/math]
- Die Ortsfunktion und ihre zweite Ableitung kann man nun in die DGL einsetzen und überprüfen, ob die Gleichung stimmt:
- [math] \begin{align} && 0{,}1\,{\rm kg}\,\cdot 0\,{\rm\tfrac{m}{s^2}} &= -0{,}4\,{\rm\tfrac{N}{m}} \cdot 0\,{\rm m}\\ \Leftrightarrow && 0\,{\rm kg\,\tfrac{m}{s^2}} &= 0\,{\rm N}\\ \end{align} [/math]
- Diese Aussage ist wahr! Das Ortsgesetz [math]y_1(t)[/math] ist also eine Lösung der DGL.
- Anschaulich bedeutet das, dass der Wagen in der Ruhelage stehen bleiben kann, was einleuchtet, denn dort wirkt keine Kraft auf ihn.
- [math]y_2(t)=0{,}01\,{\rm m} \quad \Rightarrow \quad \ddot y_1(t) = 0\,{\rm\tfrac{m}{s^2}}[/math]
- In die DGL einsetzen:
- [math] \begin{align} && 0{,}1\,{\rm kg\,\cdot 0\,\rm\tfrac{m}{s^2}} &= -0{,}4\,{\rm\tfrac{N}{m}} \cdot 0{,}01\,{\rm m}\\ \Leftrightarrow && 0\,{\rm kg\,\tfrac{m}{s^2}} &= -0{,}004\,{\rm N}\\ \end{align} [/math]
- Diese Aussage ist nicht wahr! Das Ortsgesetz [math]y_2(t)[/math] ist keine Lösung der DGL.
- Anschaulich bedeutet das, dass der Wagen einen Zentimeter rechts von der Ruhelage nicht stehen bleiben kann. Das leuchtet ein, denn dort wirkt eine Rückstellkraft von [math]0{,}004\,\rm N[/math] nach links auf ihn.
- [math]y_3(t)=0{,}01\,{\rm m} \cdot \sin(1\,{\rm Hz}\cdot t) \quad \Rightarrow \quad \dot y_3(t) = 0{,}01\,{\rm m}\cdot 1\,{\rm Hz}\cdot \cos(1\,{\rm Hz}\cdot\,t) \quad \Rightarrow \quad \ddot y_3(t) = -0{,}01\,{\rm m\,Hz^2}\cdot \sin(1\,{\rm Hz}\cdot\,t) [/math]
- In die DGL einsetzen:
- [math] \begin{align} && -0{,}1\,{\rm kg}\cdot 0{,}01\,{\rm m\,Hz^2}\cdot \sin(1\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}01\,{\rm m} \cdot \sin(1\,{\rm Hz}\cdot t) \\ \Leftrightarrow && -0{,}001\,{\rm kg\,\tfrac{m}{s^2}}\cdot \sin(1\,{\rm Hz}\cdot\,t) &= -0{,}004\,{\rm N} \cdot \sin(1\,{\rm Hz}\cdot t) \end{align} [/math]
- Diese Aussage ist nicht wahr! Das Ortsgesetz [math]y_3(t)[/math] ist keine Lösung der DGL.
- Der Wagen kann also nicht mit einer Amplitude von 1cm und einer Periodendauer von [math]T=2\pi\,{\rm s}\approx 6\,{\rm s}[/math] schwingen.
- [math]y_4(t)=0{,}01\,{\rm m} \cdot \sin(2\,{\rm Hz}\cdot t) \quad \Rightarrow \quad \dot y_4(t) = 0{,}01\,{\rm m}\cdot 2\,{\rm Hz}\cdot \cos(2\,{\rm Hz}\cdot\,t) \quad \Rightarrow \quad \ddot y_4(t) = -0{,}04\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) [/math]
- In die DGL einsetzen:
- [math] \begin{align} && -0{,}1\,{\rm kg}\cdot 0{,}04\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}01\,{\rm m} \cdot \sin(2\,{\rm Hz}\cdot t) \\ \Leftrightarrow && -0{,}004\,{\rm kg\,\tfrac{m}{s^2}}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}004\,{\rm N} \cdot \sin(2\,{\rm Hz}\cdot t) \end{align} [/math]
- Diese Aussage ist wahr! Das Ortsgesetz [math]y_4(t)[/math] ist eine Lösung der DGL.
- Der Wagen kann also mit einer Amplitude von 1cm und einer Periodendauer von [math]T=\pi\,{\rm s}\approx 3\,{\rm s}[/math] harmonisch schwingen.
- [math]y_5(t)=0{,}01\,{\rm m} \cdot \cos(2\,{\rm Hz}\cdot t) \quad \Rightarrow \quad \ddot y_5(t) = -0{,}04\,{\rm m\,Hz^2}\cdot \cos(2\,{\rm Hz}\cdot\,t) [/math]
- In die DGL einsetzen:
- [math] \begin{align} && -0{,}1\,{\rm kg}\cdot 0{,}04\,{\rm m\,Hz^2}\cdot \cos(2\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}01\,{\rm m} \cdot \cos(2\,{\rm Hz}\cdot t) \\ \Leftrightarrow && -0{,}004\,{\rm kg\,\tfrac{m}{s^2}}\cdot \cos(2\,{\rm Hz}\cdot\,t) &= -0{,}004\,{\rm N} \cdot \cos(2\,{\rm Hz}\cdot t) \end{align} [/math]
- Diese Aussage ist wahr! Das Ortsgesetz [math]y_5(t)[/math] ist eine Lösung der DGL.
- Im Unterschied zu [math]y_4(t)[/math] beginnt die Bewegung mit einer maximalen Auslenkung. Der Wagen wird also 1cm nach rechts ausgelenkt und bei [math]t=0\,\mathrm s[/math] losgelassen.
- [math]y_6(t)=0{,}05\,\mathrm{cm} \cdot \sin(2\,{\rm Hz}\cdot\,t) \quad \Rightarrow \quad \ddot y_6(t) = -0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) [/math]
- In die DGL einsetzen:
- [math] \begin{align} && -0{,}1\,{\rm kg}\cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}05\,{\rm m} \cdot \sin(2\,{\rm Hz}\cdot t) \\ \Leftrightarrow && -0{,}02\,{\rm kg\,\tfrac{m}{s^2}}\cdot \sin(2\,{\rm Hz}\cdot\,t) &= -0{,}02\,{\rm N} \cdot \sin(2\,{\rm Hz}\cdot t) \end{align} [/math]
- Diese Aussage ist wahr! Das Ortsgesetz [math]y_6(t)[/math] ist eine Lösung der DGL.
- Der Wagen kann also mit einer Amplitude von 5cm und einer Periodendauer von [math]T=\pi\,{\rm s}\approx 3\,{\rm s}[/math] harmonisch schwingen.
- [math]y_7(t)=5\,\rm cm \cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) \quad \Rightarrow \quad \ddot y_6(t) = -0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) [/math]
- In die DGL einsetzen:
- [math] \begin{align} && -0{,}1\,{\rm kg}\cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) &= -0{,}4\,{\rm\tfrac{N}{m}}\cdot0{,}05\,{\rm m} \cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4})\\ \Leftrightarrow && -0{,}02\,{\rm kg\,\tfrac{m}{s^2}}\cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) &= -0{,}02\,{\rm N} \cdot 0{,}20\,{\rm m\,Hz^2}\cdot \sin(2\,\rm Hz\cdot\,t +\tfrac{2\pi}{4}) \end{align} [/math]
- Diese Aussage ist wahr! Das Ortsgesetz [math]y_7(t)[/math] ist eine Lösung der DGL.
- Der Wagen schwingt harmonisch mit einer Amplitude von 5cm und einer Periodendauer von [math]T=\pi\,{\rm s}\approx 3\,{\rm s}[/math]. Durch die Addition von [math]\tfrac{2\pi}{4}[/math] wird der Zeiger zusätzlich um 90° gedreht, wodurch die Bewegung mit maximaler Auslenkung nach rechts beginnt, genau so wie bei [math]y_5(t)[/math]. Das ergibt sich auch aus dem mathematischen Zusammenhang: [math]\sin(t+\tfrac{2\pi}{4})=\cos(t)[/math].
c) Erläutern Sie die physikalische Bedeutung der rechnerischen Ergebnisse von b).
- Steht bereits oben bei b).
Die DGL für die speziellen Werte von Masse und Federhärte kann man verallgemeinern:
- [math]m \, \ddot y(t) = - D \, y(t)[/math]
d) Leiten Sie daraus die Formel für die Periodendauer des schwingenden Wagens ab:
- [math]T = 2 \pi \sqrt{\frac{m}{D}}[/math]
- Als mögliche Lösung nimmt man eine harmonische Schwingung mit einer beliebigen Amplitude [math]\hat y[/math] und einer beliebigen Kreisfrequenz [math]\omega[/math] und setzt sie in die DGL ein:
- [math] y(t)=\hat y \, \sin(\omega \,t) \quad \Rightarrow \quad \ddot y(t) = -\hat y \,\omega^2 \,\sin(\omega t)[/math]
- [math]m \,\omega^2 \hat y \, \sin(\omega \,t) = - D \, \hat y \, \sin(\omega \,t)[/math]
- Man sieht, dass die Gleichung nur dann stimmt, wenn [math]m \,\omega^2 = D [/math] gilt. Das kann man noch umformen und nach [math]T[/math] auflösen:
- [math] \begin{align} &&m \,\omega^2 = D &&|:m\\ \Leftrightarrow &&\omega^2 = \frac{D}{m} &&& \textrm{mit }\omega=\frac{2\pi}{T}\\ \Leftrightarrow &&\left(\frac{2\pi}{T}\right)^2 = \frac{4\pi^2}{T^2} = \frac{D}{m} \\ \Leftrightarrow && \frac{T^2}{4\pi^2} = \frac{m}{D} &&|\cdot 4\pi^2 \\ \Leftrightarrow && T^2 = 4\pi^2 \,\frac{m}{D} &&|\sqrt{\quad}\\ \Leftrightarrow && T = 2 \pi \sqrt{\frac{m}{D}}\\ \end{align} [/math]
e) Begründen Sie, dass die Frequenz nicht von der Amplitude der Schwingung abhängt.
- In der gefundenen Lösung der DGL hängt die Kreisfrequenz zwar von der Federhärte und der Masse ab, aber nicht von der Amplitude.
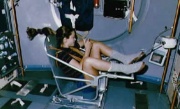
11) Eine "Schwingungswaage"
- Erläutern Sie, warum man mit dieser Waage die Masse der Astronautin bestimmen kann. Benutzen Sie hierfür die Begriffe Trägheit und beschleunigende Kraft/Rückstellkraft.
Mit dieser Waage kann die Trägheit, also die träge Masse der Astronautin gemessen werden. Die beschleunigende Kraft (und damit die Impulsänderung) ist durch die Feder vorgegeben, verändert sich also nicht bei unterschiedlichen Massen. Bei einer größeren Masse wird sich daher die Geschwindigkeit weniger schnell verändern, was sich in einer niedrigeren Frequenz der Schwingung äußert.
- Wie verändert sich die Frequenz, wenn man die Amplitude der Schwingung verändert? Warum ist das für die Weltraumwaage sehr praktisch?
Die Frequenz einer Federschwingung hängt nicht von der Amplitude ab. Das ist praktisch, weil es für die Messung irrelevant ist, wie stark die Astronautin "angeschubst" wird.
Der leere Stuhl hat eine Masse von [math]m_0=2\, \rm kg[/math] und schwingt mit einer Periode von [math]T=0{,}33\, \rm s[/math].
- Bestimmen Sie hieraus die Härte [math]D[/math] der Feder.
Den Zusammenhang zwischen Winkelgeschwindigkeit, Federhärte und Masse kann man nach der Federhärte auflösen:
- [math] \begin{array}{rcll} \omega^2 &=& \frac{D}{m} & | \cdot m \\ D &=& \omega^2\, m & | \ \omega =\frac{2\pi}{T}\\ &=& \frac{4 \pi^2}{T^2} \, m\\ &=& \frac{4 \pi^2}{(0{,}33\, \rm s)^2} \cdot 2\, \rm kg \\ &=& 725 \frac{\rm N}{\rm m} & \left[ \rm { \frac{kg}{s^2}=\frac{kg\,m}{m\, s^2}=\frac{kg\,\frac{m}{s^2}}{m} = \frac{N}{m} } \right] \end{array} [/math]
Nun steigt die Astronautin in den Stuhl und die Periodendauer verlängert sich auf [math]T=1{,}87\, \rm s[/math].
- Welche Masse hat die Astronautin?
Diesmal löst man nach der Masse auf:
- [math] \begin{array}{rcll} \omega^2 &=& \frac{D}{m} & | \cdot m \ |\colon \omega^2\\ m &=& \frac{D}{\omega^2}& | \ \omega =\frac{2\pi}{T}\\ &=& \frac{D\, T^2}{4 \pi^2} \\ &=& \frac{725 \frac{\rm N}{\rm m} \, (1{,}87\, \rm s)^2}{4 \pi^2} \\ &=& 64{,}22\,\rm kg & \left[ \rm { \frac{N\,s^2}{m}= \frac{kg\,\frac{m}{s^2}\,s^2}{m}=kg} \right]\\ \end{array} [/math]
Das ist die Masse von Astronautin und Stuhl, von der man noch die Stuhlmasse abziehen muss. Die Astronautin hat also eine Masse von [math]62{,}22\,\rm kg[/math].
Man kann die Masse der Astronautin auch ohne den Zwischenschritt über die Federhärte berechnen. An der Gleichung [math]m = \frac{D\, T^2}{4 \pi^2} [/math] erkennt man, dass die Masse proportional zum Quadrat der Schwingungsdauer ist:
- [math] m \sim T^2 [/math]
Das Verhältnis der Masse zum Quadrat der Schwingungsdauer ist daher immer gleich groß:
- [math] \begin{array}{rcll} \frac{m_{ges}}{{T_{ges}}^2 } &=& \frac{m_{Stuhl}}{{T_{Stuhl}}^2} & | \cdot {T_{ges}}^2 \quad \text{nach}\, m_{ges} \, \text{auflösen}\\ m_{ges} &=& \frac{{T_{ges}}^2}{{T_{Stuhl}}^2} \, m_{Stuhl} \\ &=& \frac{(1{,}87\, \rm s)^2}{(0{,}33\, \rm s)^2} \cdot 2\,\rm kg \\ &=& 32{,}11 \cdot 2\,\rm kg \\ \end{array} [/math]
In einem Modellversuch schwingt ein Wagen zwischen zwei Federn. Die Federkonstante einer Feder beträgt [math]3\,\rm \frac{N}{m}[/math]. Zusammen wirken sie wie eine Feder mit der doppelten Federkonstante. Der Wagen hat eine Masse von [math]190{,}6\,\rm g[/math].
- Wie schwer ist eine am Wagen befestigte Batterie, wenn der Wagen mit ihr nun in 5,6 Sekunden viermal schwingt?
Löst man die Formel für die Frequenz einer harmonischen Schwingung nach der Masse auf, so erhält man:
- [math]f = \frac{1}{2 \pi} \sqrt{\frac{D}{m}} \quad \Rightarrow \quad m= \frac{D}{4 \pi^2 \, f^2}[/math]
Mit [math]f = \frac{4}{5,6 \rm \, s} = 0,714 \,\rm Hz[/math] folgt:
- [math]m= \frac{2\cdot 3 \,\rm N/m}{4 \pi^2 \, (0,714 \,\rm 1/s)^2} = 0,298\, \rm kg[/math]
Das ist die Masse des Wagens und der Batterie zusammen. Die Batterie hat also eine Masse von [math]298\, \rm g - 190,6 \, \rm g \approx 107 g[/math]!
12) Schaukeltier II
Große Kinder haben eine größere Masse, wodurch sie "langsamer", also mit einer geringeren Frequenz, schwingen!
13) Schwingmännchen III
Das Männchen bringt 200g auf die Waage und verlängert beim Dranhängen die vorher unbelastete Feder um 40cm.
- Wieso beträgt die Federkonstante (D) gerade 1/20 N/cm = 0,05 N/cm?
- Die Gewichtskraft von 200g beträgt ca. 2 Newton:
- [math]F_G = m \, g = 0{,}200\,\rm kg \cdot 9,81 \frac{\rm N}{\rm kg} \approx 2\,\rm N[/math]
Die Federkonstante gibt die benötigte Kraft pro Verlängerung an:
- [math]D=\frac{\rm Kraft}{\rm Verl\ddot a ngerung}=\frac{2\, \rm N}{40 \,\rm cm}=0{,}05\frac{\rm N}{\rm cm} =5\frac{\rm N}{\rm m} [/math]
- Mit welcher Frequenz wird das Männchen schwingen?
- Mit [math]\omega ^2 = \frac{D}{m}[/math] folgt:
- [math]f = \frac{1}{2 \, \pi}\sqrt{\frac{D}{m}}= \frac{1}{2 \, \pi} \sqrt{\frac{5\,\rm N/m}{0{,}2\,\rm kg}}\approx 0{,}80 \,\rm Hz [/math]
- Es schwingt etwas weniger als einmal pro Sekunde.
- Muss man ergänzen oder bei Aufgaen entfernen, da es sich mit A14 überschneidet (An Inhaber der Website)
14) Schwingmännchen IV
Um die Frequenz zu verdoppeln, muss man die Federhärte vervierfachen, also ein Viertel der Feder benutzen, oder die Masse vierteln.
15) Schwingmännchen V
| Es gilt: | [math]\omega = 2\ \Pi \ f=\sqrt{\frac{D}{m}}[/math] | [math]E=\frac{1}{2}\, m \ (\omega \hat y)^2 = \frac{1}{2}D\ \hat y^2[/math] |
| *die Federkonstante verdoppelt: | Die Frequenz erhöht sich um den Faktor [math]\sqrt{2}[/math]. | Der Energiegehalt verdoppelt sich. |
| *die Masse verdoppelt: | Die Frequenz verringert sich um den Faktor [math]\sqrt{2}[/math]. | Der Energiegehalt bleibt gleich! (Das Männchen ist zwar schwerer, schwingt aber dafür langsamer.) |
| *die Amplitude verdoppelt: | Die Frequenz bleibt gleich! | Der Energiegehalt vervierfacht sich. |
16) Schaukeltier III
Beim Anschubsen müssen die Kinder im richtigen Rythmus, nämlich in der Eigenfrequenz anregen, sonst nimmt die Schwingung die Energie nicht an und der Effekt ist gering! Zu schnelles Anschubsen bringt also nichts.
17) Schwingungskategorien
Da finden sich im Kapitel Energiezufuhr bei Schwingungen Beispiele.
18) Wackelnder Rückspiegel
- Ich kann die Anregungsfrequenz verändern, also langsamer oder schneller fahren.
- Ich kann die Eigenfrequenz des Spiegels ändern, indem ich z.B. seine Masse vergrößere. (Das könnte man mit Knete oder einer Wäschklammer erreichen, dann verringert sich die Eigenfrequenz.)
- Ich kann den Spiegel dämpfen und ihm die Energie entziehen, z.B. indem ich mit dem Finger dranfasse. (Das ist die einzige Lösung, die dauerhaft bei allen Geschwindigkeiten funktioniert.)
19) harmonische Schwingung
Das kann man im Kapitel Woran man eine harmonische Schwingung erkennt lesen.
20) Energie
Geg:[math]m = 1kg[/math]
- [math]T = 1s[/math]
- [math]\hat y = 0,01m[/math]
Ges: [math]E[/math]
Rechnung: Entweder man setzt in die fertige Formel ein:
- [math]E_{kin}=\frac{1}{2}\, m\,(\hat y\, \omega)^2 = E_{kin}=\frac{1}{2}\, m\,(\hat y\, 2\pi\, f)^2[/math]
Oder man überlegt es sich noch einmal selbst:
Die maximale Bewegungsenergie ist auch die Gesamtenergie der Schwingung:
- [math]E_{kin}=\frac{1}{2}\, m\,\hat v^2[/math]
Die maximale Geschwindigkeit beträgt:
- [math]\hat v = \hat y \, \omega = \hat y \, 2\pi f = 0{,}01\, \rm m \cdot 2\pi \cdot 1\,\rm Hz = 0{,}0628\,\rm m/s[/math]
Jetzt noch einsetzen:
- [math]E_{kin}=\frac{1}{2}\cdot 1\,\rm kg \cdot \hat (0{,}0628\,\rm m/s)^2 \approx 0{,}002\,\rm J [/math]
Das ist sehr wenig!
22) Energie II
Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat?
Dazu muss man eine Frequenz und eine Amplitude finden. Je größer Frequenz und Amplitude, desto mehr Energie ist in der Schwingung.
Es soll also gelten:
- [math]E = \frac{1}{2} \ 1kg (2 \ \Pi \ f \ \hat y)^2 = 1 J[/math]
Multipliziert man die Gleichung mit 2 folgt für die Frequenz und die Amplitude:
- [math](2 \ \Pi \ f \ \hat y)^2 = 2 \frac{m^2}{sec^2}\qquad.[/math] Nun noch die Wurzel ziehen:
[math]\Rightarrow 2 \ \Pi \ f \ \hat y = \sqrt{2} \frac{m^2}{sec^2}[/math]
[math]\Rightarrow \ f \ \hat y =\frac{\sqrt{2}}{2 \ \Pi} \frac{m^2}{sec^2} \approx 0,225 \frac{m^2}{sec^2}[/math]
Für eine Frequenz von 1 Hz ergibt sich eine Amplitude von 0,23 m = 23 cm. Für eine Amplitude von nur 1cm = 0,01 m benötigt man schon eine Frequenz von ca 23 Hz.
23) Energie III
Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen.
Für die Energie gilt: [math]E=\frac{1}{2} \ m \ (\omega \ \hat y)^2 = \frac{1}{2} \ m \ (2 \ \Pi \ f \ \hat y)^2[/math]
Die Energie ist also proportional zum Quadrat der Frequenz. Bei einer Verdoppelung wird sich der Energiegehalt vervierfachen!
24) Zwei schwingende Wagen
Wenn die Wagen schwingen haben sie zu unterschiedlichen Phasen der Schwingung unterschiedlich viel Impuls. Der Impuls nach rechts soll als positiv gewertet werden.
Ebenso ändert sich die Energiemenge in der Feder und in den Wagen.
- Ergänze in der Tabelle qualitativ die Angaben von Impuls und Energie.
25) Wasserstoffmolekül
Ein H2-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 1011 Hz.
- Bestimmen sie die "Federkonstante" der gedachten Feder zwischen den Molekülen.
Wie die Moleküle im Modell schwingen, kann man hier sehen. Wichtig ist, dass beide Atome mit der gleichen Frequenz schwingen.
Die Situation ist symmetrisch und man betrachtet für die Rechnung die Hälfte des Versuchsaufbaus. Durch die Halbierung der Feder verdoppelt sich dann die berechnete Federkonstante.
Die Masse eines H-Atoms beträgt ca. [math]1{,}66 \cdot 10^{-27}\,\mathrm{kg}[/math].
Zwischen Kreisfrequenz, Federkonstante und Masse besteht der Zusammenhang: [math]\omega^2 = \frac{D}{m} \quad \Rightarrow \quad D = \omega^2 \, m = 4 \pi^2 \, f^2 \, m [/math]
- [math]D = 4 \pi^2 \, (9{,}2\cdot10^{11}\,\rm Hz)^2 \cdot 1{,}66 \cdot 10^{-27}\,\mathrm{kg}= 0,055 \frac{\rm N}{\rm m}[/math]
Die gesamte Feder hätte somit eine Federkonstante von [math]0,028 \frac{\rm N}{\rm m}[/math]. Makroskopisch wäre das eine sehr schwache Feder. Für das "kleine" Wasserstoffatom ist das aber eine sehr starke Kopplung.
- Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10-10m schwingen?
Die Energie einer Hälfte ergibt sich zu:
- [math]E = \frac{1}{2}\, m \, \hat y^2 \, \omega^2 = \frac{1}{2}\, 1{,}66 \cdot 10^{-27}\,\mathrm{kg} \, ( 10^{-10}\,\rm m)^2 \, (2 \pi \, 9{,}2\cdot10^{11}\,\rm Hz)^2 = 2{,}8\cdot 10^{-22}\,\rm J[/math]
- [math]E_{ges}=5{,}6 \cdot 10^{-22}\,\rm J[/math]
Makroskopisch nicht viel, aber bei einem Mol, also [math]6{,}022 \cdot 10^{23}[/math] Molekülen, immerhin ca. [math]340 \, \rm J[/math]!
26) Molekül-Spektroskopie
- Bei großen oder langen Molekülen findet man viele Frequenzen, bei denen die Energie nicht auf der anderen Seite ankommt. Bei einem Molekül wie Kohlenmonoxid (CO) nur eine. Wie kann man das erklären?
- Das CO-Molekül hat nur eine Eigenschwingung mit einer Eigenfrequenz. Dabei schwingen die Atome aufeinander zu und wieder weg. Größere Moleküle verhalten sich wie ausgedehnte Körper, etwa eine Stange oder eine Platte. Deswegen haben sie viele Eigenschwingungen und viele Eigenfrequenzen.
- Wird die Energie in der "passenden" Frequenz zugeführt, so nimmt das Molekül viel Energie auf und gibt sie dann wieder ab. Dabei wird die Energie aber nicht mehr in der ursprünglichen Richtung weitergeleitet und auch die Frequenz kann sich ändern.
- Bei Kohlenmonoxid misst man eine Absorption bei der Frequenz [math]f=6{,}5\cdot 10^{13}\,\rm Hz[/math]. Als Modell für das Molekül kann man vereinfachend zwei punktförmige Massen annehmen, die mit einer masselosen Feder verbunden sind. (So wie hier.)
- Bestimmen Sie die "Federkonstante" des Moleküls.
Die Massen der Atome betragen in etwa: [math]m_C = 12\,\rm u[/math] und [math]m_O = 16\, \rm u[/math], mit [math]u=1{,}66\cdot 10^{-27}\,\rm kg[/math].
Beide Atome schwingen mit der gleichen Frequenz. Der Schwerpunkt liegt dabei näher am massereicheren O-Atom und bleibt erhalten. Das Verhältnis der Abstände zwischen Atom und Schwerpunkt beträgt 16 zu 12 oder 4 zu 3. Nun kann man entweder die Schwingung des C-Atoms betrachten und die Federkonstante diesen Teils der Feder berechnen oder eben den Teil des O-Atoms. Für das Sauerstoffatom gilt:
- [math]\omega^2=\frac{D_O}{m} \quad \Rightarrow \quad D = \omega^2 \, m = 4\pi^2\, (6{,}5\cdot 10^{13}\,\rm Hz)^2 \cdot 16\cdot 1{,}66\cdot 10^{-27}\,\rm kg = 4430 \frac{\rm N}{\rm m}[/math]
- Dies ist die Federhärte von [math]3/7[/math] der Feder. Die ganze Feder ist um den Faktor [math]7/3[/math] länger und somit weniger hart, die Federhärte der gesamten Feder beträgt:
- [math]D= 4430 \frac{\rm N}{\rm m}: \frac{7}{3} = 1900 \frac{\rm N}{\rm m}[/math]
Genauere Informationen findet man im Artikel "Infrarotspektroskopie" bei Wikipedia oder Interessantes zum Verhalten von CO_2 beim Treibhauseffekt in diesem Artikel der Chemiedidaktik Bayreuth zu Grundlagen der IR-Spektroskopie (nicht mehr online??).
27) Schwebung von Stimmgabeln
Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz, die andere hat eine Frequenz von 438 Hz.
Was kann man hören?
- Man hört eine Schwebung mit einer Frequenz von 2Hz. Also einen Ton, der zweimal pro Sekunde laut und zweimal pro Sekunde leise ist.
28) Schwebung
Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz. Schätzen Sie die Frequenz der anderen Stimmgabel ab.
Lösung:
Das Schätzen der Frequenz der anderen Stimmgabel wäre äußerst schwierig, da die Frequenz wohl viel zu hoch wäre. Man kann aber die Frequenz der Schwebung abschätzen. In unserem Beispiel ergab dies etwa [math]1{,}2\,\rm Hz[/math]. Da die Frequenz der zweiten Stimmgabel geringer sein wird, als die der anderen (der Reiter verlangsamt die Schwingung, indem er zusätzliche Masse einbringt) und die Frequenz der Schwebung gerade die Differenz der Frequenzen der beiden Stimmgabeln ist, ergibt sich:
[math]\rm 440\,\rm Hz - x\,\rm Hz=1{,}2\,\rm Hz \Rightarrow x=438{,}8[/math]
Die zweite Stimmgabel hat also etwa die Frequenz [math]438{,}8\,\rm Hz[/math].
29) Überlagerung
Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y1 und y2 entsteht mit Hilfe des Zeigerdiagramms:
Beide Schwingungen haben die selbe Winkelgeschwindigkeit ([math]\omega = 2\,\rm Hz[/math]). Die zweite Schwingung ist um [math]\pi[/math] phasenverschoben, also genau gegenphasig.
Da die Schwingungen gegenphasig sind, eliminieren sie sich gegenseitig, da die zweite Schwingung aber die doppelte Amplitude der ersten Schwingung hat, wird ein Ton mit der halben Amplitude der zweiten Schwingung, aber ohne Phasenverschiebung zu dieser hörbar sein.
Die neue Amplitude, also die Zeigerlänge des Summenvektors, kann man mit dem Satz des Pythagoras berechnen:
- [math]\hat y = \sqrt{(2\,\rm cm)^2+(4\,\rm cm)^2} \approx 4{,}47\,\rm cm[/math]
Die Phasenverschiebung [math]\alpha[/math] zur Schwingung Nr.1 (roter Zeiger) ergibt sich aus dem Tangens im rechtwinkligen Dreieck:
- [math]\tan(\alpha)= 4\,\rm cm / 2\,\rm cm = 2 \quad \Rightarrow \quad \alpha = \arctan(2)\approx 1{,}11 \quad (\hat = 63{,}4^\circ)[/math]
Also hat die Überlagerung der Schwingungen die Schwingungsgleichung:
- [math]y=4{,}47\,\rm cm \cdot \sin(2\, t + 1{,}11)[/math]
Da die Zeiger entgegengesetzt gleich sind, heben sich die beiden Schwingungen gerade auf.
Schwieriges und Anderes
7 Schwingung bei bekannter Energie
Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird?
Gegeben: [math]m =0{,}6\,\rm kg \qquad D=100\,\frac{\rm N}{\rm m} \qquad E=1\,\rm J [/math]
Die Charakteristik einer Schwingung definieren wir als Angabe von der Frequenz [math]f[/math] und der Amplitude [math]\hat y[/math].
Es wird mit der doppelten Federstärke [math]D[/math] gerechnet, da wir den Fall auf nur einen Wagen idealisieren (Stille Annahme: Symmetrie der Bewegung).
Zunächst widmen wir uns der Frequenz [math]f[/math]:
- [math]f=[/math][math]{\omega}\over 2\pi[/math][math]=[/math][math]\sqrt {2D \over m}\over 2\pi[/math][math]=[/math][math]\sqrt {{200 {N\over m}} \over 0.6kg}\over 2\pi[/math][math]=[/math][math]2.91Hz[/math]
Nun zur Amplitude [math]\hat y[/math]:
- [math]E_{pot}=[/math][math]2\left({2D\over 2}{\hat y}^2\right)[/math]
- [math]\hat y=[/math][math]\sqrt {E\over 2D}[/math][math]=[/math][math]\sqrt {1Jm\over {200N}}[/math][math]=[/math][math]{0.1\over{\sqrt 2}}m[/math][math]=[/math][math]0.07m[/math]
(für einen einzelnen Wagen; das Gesamtsystem hat jedoch 2[math]\hat y[/math])
9 Ekin = ESpann
Es wird gefragt für welche Auslenkung die Energie gleichermaßen in dem Impuls als auch in der Feder ist. Also wann die kinetische Energie gerade gleich der kinetischen bzw. der Spannenergie ist.
Bei der gleichmäßigen Verteilung der Energie auf die Bewegung und die Feder, enthält sowohl die Feder als auch die Bewegung gerade die Hälfte der Energie:
- [math]E_{pot}= \frac{1}{2}\, E_{ges}[/math]
- [math]\frac{1}{2} \, D\, y^2 = \frac{1}{2}\,\frac{1}{2} D \, \hat y^2[/math]
- nach y aufgelöst:
- [math]y=\frac{1}{\sqrt{2}} \, \hat y \approx 0,7 \, \hat y[/math]
Bei ca. 70% der Amplitude ist die Energie gleichmäßig auf Bewegung und Feder verteilt.
10 Zeitlicher Mittelwert von Ekin und ESpann
Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel.