Gleichförmige Bewegung mit konstantem Impuls (Kräftegleichgewicht; Fließgleichgewicht): Unterschied zwischen den Versionen
(→Animation: Kräftegleichgewicht im Wasserbehältermodell) |
|||
| (4 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Kräfte_ändern_den_Impuls|'''Kräfte ändern den Impuls''']]) | |
| + | ==Beispiele== | ||
<gallery widths=200px heights=133px perrow=4 > | <gallery widths=200px heights=133px perrow=4 > | ||
Bild:Inliner fahren.jpg|Mit guten Inlinern und einem glatten Boden kann man auch ohne sich anzuschubsen gut rollen. | Bild:Inliner fahren.jpg|Mit guten Inlinern und einem glatten Boden kann man auch ohne sich anzuschubsen gut rollen. | ||
| Zeile 6: | Zeile 7: | ||
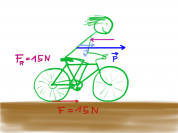
Bild:Bewegung Wassermodell Fahrad.png|Hört man beim Radfahren auf zu treten, so rollt man weiter, verliert aber langsam seinen Impuls. | Bild:Bewegung Wassermodell Fahrad.png|Hört man beim Radfahren auf zu treten, so rollt man weiter, verliert aber langsam seinen Impuls. | ||
Bild:Bewegung_Wassermodell_Fahrrad_Behälter.png|Man kann aber auch mit konstanter Geschwindigkeit fahren! | Bild:Bewegung_Wassermodell_Fahrrad_Behälter.png|Man kann aber auch mit konstanter Geschwindigkeit fahren! | ||
| − | Bild: | + | Bild:Supraleitung_Schwebebahn_Uni_Zürich_Standbild.jpg|Diese tiefgekühlten Supraleiter gleiten auf einem Magnetfeld. ([https://www.youtube.com/watch?v=c3TvJlJ2QTY Video der EZH Zürich]) |
Bild:| | Bild:| | ||
</gallery> | </gallery> | ||
| Zeile 22: | Zeile 23: | ||
Das Fixpunktdiagramm stellt die Zufluss- und Abflussrate in Abhängigkeit von der Höhe des Wasserspiegels dar. | Das Fixpunktdiagramm stellt die Zufluss- und Abflussrate in Abhängigkeit von der Höhe des Wasserspiegels dar. | ||
| − | |||
{{#widget:Iframe | {{#widget:Iframe | ||
| − | |url=https:// | + | |url=https://www.geogebra.org/material/iframe/id/KZezmyH2/width/1000/height/730/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false |
|width=750 | |width=750 | ||
|height=548 | |height=548 | ||
| Zeile 89: | Zeile 89: | ||
|} | |} | ||
| + | ==Links== | ||
| + | *Video: [https://www.youtube.com/watch?v=c3TvJlJ2QTY Schwebebahn mit Hochtemperatur-Supraleitung] (youtube: "Universität Zürich") | ||
==Fußnoten== | ==Fußnoten== | ||
<references /> | <references /> | ||
Aktuelle Version vom 9. August 2025, 10:53 Uhr
(Klassische Mechanik > Kräfte ändern den Impuls)
Inhaltsverzeichnis
Beispiele
[1] Noch schneller geht es mit Schlittschuhen.
Diese tiefgekühlten Supraleiter gleiten auf einem Magnetfeld. (Video der EZH Zürich)
Um bei einer Bewegung die Impulsmenge konstant zu halten, darf entweder gar keine Kraft wirken und somit kein Impuls verloren gehen. Das ist bei Bewegungen mit wenig Reibung annähernd der Fall.
Oder die Reibungskraft muss genau ausgeglichen werden, damit die Kraftsumme Null ist und somit genausoviel Impuls dazukommt wie weg geht.
Animation: Kräftegleichgewicht im Wasserbehältermodell
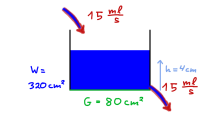
Eine Wasserpumpe pumpt Wasser in einen Behälter, der einen Abfluß hat.
Mit den Schiebereglern unter dem Behälter kann man die Bedingungen verändern. Der linke steuert die Zuflussrate, der rechte durch die Größe des Abflußrohres, die Abflussrate. In der Mitte kann man die Behältergröße einstellen.
Das Fixpunktdiagramm stellt die Zufluss- und Abflussrate in Abhängigkeit von der Höhe des Wasserspiegels dar.
Bewegungsgesetze herleiten
Die folgende Aufgabe kann man mit dieser Animation der Bewegungsdiagramme lösen!
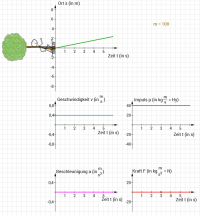
Pauline fährt mit konstanter Geschwindigkeit von 0,8 m/s und hat eine Masse von 50 kg. Als sie am Baum vorbeifährt, beginnt die Zeitmessung. Die Reibung soll zunächst vernachlässigt werden.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wo ist Pauline nach 6 Sekunden und wie schnell ist sie?
- c) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
[math]s(t) = v_0\, t = 0{,}8 \, \rm{\frac{m}{s}} \cdot t[/math] [math]v(t) = v_0 = 0{,}8 \, \rm \frac{m}{s} [/math] [math]p(t) = m\,v_0 = 40 \, \rm Hy [/math] [math]a(t) = 0 \, \rm \frac{m}{s^2}[/math] [math]F(t) = 0 \, \rm N[/math]
- d) Löse b) mit Hilfe der Bewegungsgesetze.
Bewegungsgesetze der gleichförmigen Bewegung
Links
- Video: Schwebebahn mit Hochtemperatur-Supraleitung (youtube: "Universität Zürich")
Fußnoten
- ↑ Ausschnitt aus einem Bild von Robert Scoble-CC BY 2.0