Das Oszilloskop: Unterschied zwischen den Versionen

Version vom 23. Mai 2012, 15:08 Uhr

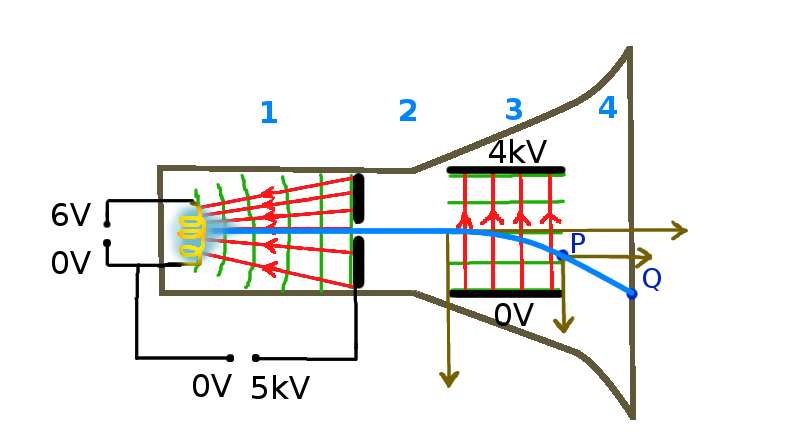
Schema

1. Die Elektronen werden beschleunigt.

2. Die Elektronen bewegen sich mit einer konstanten Geschwindigkeit.

3. Die senkrechte Geschwindigkeitskomponente nimmt konstant zu. Die horizontale bleibt konstant. Die Elektronen bewegen sich auf einer Parabel ähnlich dem waagrechten Wurf.

4. Bewegung mit konstanter Geschwindigkeit.

Rechnerische Behandlung

Hier werden zwei Fragen behandelt:

  1. Wie schnell sind die Elektronen?
  2. Wie hängt die Ablenkung der Elektronen mit der angelegten Spannung zusammen? 

Geschwindigkeit der Elektronen

[math]E_{el} = E_{kin} \qquad \Leftrightarrow \qquad e \, \triangle \varphi = \frac{1}{2} m v^2_0 \qquad \Leftrightarrow \qquad v_0 = \sqrt{\frac{2\, e\, U_x}{m}[/math]

Bei einer Beschleungungsspannung von 4000 Volt erreichen die Elektronen immerhin ca 10% der Lichtgeschwindigkeit!

Bewegung im Ablenk-Kondensator

[math]x(t)=v_0 t[/math]

[math]E = {U y \over d}[/math]

[math]\begin{matrix}F&=& e E &=& m a \end{matrix}[/math]

[math]\Longrightarrow a = {e E \over m}[/math]

[math]y(t)={1 \over 2} a t^2 \ = \ {1 \over 2 } {e E \over m} t^2 \ = \ {1 \over 2 } {e U y \over m d } t^2 [/math]

Nebenüberlegung:

[math]v_x (t) = v_0 \begin{matrix} v_y (t) &=& at \\ \ &=& {e U y \over m d} t\end{matrix}[/math]

C) Punkt P: [math]\ (x_p | y_p)[/math] bestimen

[math]t_p[/math] : Zeit im Ablenkkondensator bis P

[math]x_p = l = v_0 t_p \quad \Rightarrow \quad t_p \ = {l \over v_0}[/math]

[math]\ \ \begin{matrix} y_p (t_p) &=& {1 \over 2 } \ {e U_y \over m d } \ {l^2 \over v^2_0} \\ \ &=& \ {1 \over 2 } \ {e U_y l^2 m \over m d 2 e U_x} \\ \ &=& {1 \over 4} \ {U_y \over U_x} \ {l^2 \over d}\end{matrix}[/math]

Nebenüberlegung:

für [math]\ v^2_0 \ \[/math] wird [math]\frac{ 2 e U_x}{m} [/math] eingesetzt

Berechnung von Q im KS*

zuerst wird nach der Geschwindigkeit [math]v_y[/math] gesucht, die die vertikale Geschwindigkeit im Punkt P beschreibt

[math]v_y=a*t_p=\frac{eU_Y}{md}*\frac{l}{v_x}[/math]

[math]t_q=\frac{w}{v_x}\ltbr\gt Y_q=\frac{w}{v_x}*v_y[/math]

[math]Y_q=\frac{w}{v_x}*\frac{eU_Y}{md}*\frac{l}{v_x}=\frac{U_y lw}{dU_x}[/math] weil [math]\frac{1}{(V_x)^2}= \frac{m}{2eU_x}[/math] Für den gesamten Abschnitt [math]Y_q[/math] gilt:

[math](\frac{l^2+2lw}{4d})\frac{U_y}{U_x}[/math]

deswegen ist [math]Y_q\sim U_y[/math]

Die Ablenkung des Elektronenstrahls ist proportional zur anliegenden Spannung!

Links

• Simulation der Elektronenablenkröhre zum Runterladen. (Matthias Borchert)