Ladungen im magnetischen Feld (Lorentzkraft): Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Auswertung)
(→‎Auswertung)
Zeile 72: Zeile 72:
 
|
 
|
 
Lorentzkraft auf eine senkrecht zu einem Magnetfeld bewegte elektrische Ladung:
 
Lorentzkraft auf eine senkrecht zu einem Magnetfeld bewegte elektrische Ladung:
−
:<math>F_L = \mu_0 \, H \, q \, v</math>
+
:<math>F_L = \mu_0 \, H \, Q \, v</math>
 
|}
 
|}
 +
 +
Der Zusammenhang zwischen wirkender Kraft und den Abmessungen der Kreisbahn ergibt sich aus der Mechanik der Kreisbewegungen. Die [[Dynamik_(Zentripetalkraft_und_Bahnimpuls)_der_Kreisbewegung#Für_gegebene_Bahngeschwindigkeit|Zentripetalkraft]] beträgt:
 +
:<math>F_Z=\frac{m\,v^2}{r}</math>
 +
In diesem Fall ist die Lorentzkraft ja gerade die Zentripetalkraft, also kann man die wirkende Kraft auf zwei verschiedene Arten berechnen:
 +
 +
:{|
 +
|
 +
<math>\mu_0 \, H \, e \, v =F= \frac{m\,v^2}{r}</math>
 +
|
 +
::Um die Größe des Kreises zu bestimmen, kann man nach dem Radius auflösen:
 +
|}
 +
:<math>r=\frac{m\,v^2 }{e\,\mu_0\, H \,v} =\frac{m\,v }{e\,\mu_0\, H} \quad \Rightarrow \quad r \sim \frac{v}{H}</math>
 +
Der Radius ist also proportional zur Geschwindigkeit und antiproportional zur Feldstärke. Das erklärt die Zunahme des Radius mit der Beschleunigungsspannung und die Abnahme des Radius mit ansteigender Stromstärke.
  
 
==Versuch: Elektronenstrahlen schräg zum Magnetfeld==
 
==Versuch: Elektronenstrahlen schräg zum Magnetfeld==

Version vom 7. Juli 2017, 12:12 Uhr

(Kursstufe > Elektro-Magnetismus)

Beispiele

  • In Island gibt es häufig Polarlichter zu sehen.
    (Zeitraffer-Video aus Nord-Norwegen)

  • Dieses Polarlicht in Berlin sieht man nur sehr selten.

  • Polarlichter vom Satelliten aus gefilmt. (animiert)

  • Das Magnetfeld der Erde schützt uns vor kosmischer Strahlung.
    "Sonnenstürme" können Satelliten und elektronische Geräte auf der Erde stören.

  • Krebs kann man mit Neutronenbeschuß behandeln.

  • Die Neutronenstrahlung erzeugt man mit schnellen Protonen aus einem Zyklotron.

  • Der Ringbeschleuniger HERA in Hamburg hat einen Durchmesser von einem Kilometer.

  • Die größte Maschine der Welt ist der Ringbeschleuniger des CERN in Genf. Auch er liegt unter der Erde und hat einen Durchmesser von über 4km.

Bestimmung von e/m in der Fadenstrahlröhre

Aufbau

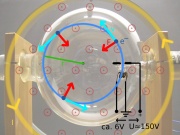
Innerhalb einer Glaskugel wird wie in einem Oszilloskop ein Elektronenstrahl erzeugt. Die Elektronen liefert, aufgrund des glühelektrischen Effekts, eine durch Strom erhitzte Glühwendel. Mit Hilfe einer Beschleunigungsspannung von ca. 150 Volt zwischen Glühwendel und Anode werden die Elektronen beschleunigt. Die Glaskugel ist von Luft evakuiert und mit Wasserstoff unter sehr niedrigem Druck von nur einem Pascal (0,01mbar) gefüllt. Durch den Wasserstoff wird der Elektronenstrahl sichtbar, denn die Elektronen regen beim Zusammenstoß mit den Wasserstoffmolekülen diese an, heben also Elektronen des Moleküls auf ein höheres Energieniveau. Fällt das Molekül-Elektron wieder auf das niedrige Niveau zurück, wird blaues Licht ausgesendet.
Der Wehneltzylinder dient der Fokussierung des Elektronenstrahls. Er liegt zylinderförmig um die Glühwendel und wird durch eine Spannung zur Glühwendel von ca. 15V negativ geladen. Die Ablenkplatten sind nicht, wie in der Gebrauchsanleitung gefordert, an die Anode angeschlossen; die Ergebnisse sind so besser.

Das Spulenpaar, "Helmholtzspule" genannt, liefert ein relativ homogenes Feld zwischen den Spulen. Der Abstand R zwischen den Spulen ist genausogroß wie der Radius der Spulen.

Die magnetische Feldstärke innerhalb der Helmholtzspule kann man entweder mit Hilfe einer Formel aus der Stromstärke und dem Spulenradius berechnen oder man misst die Feldstärke direkt mit einer Hallsonde.

  • Fadenstrahlrohr mit Spannungsversorgung für die Glühwendel und die Beschleunigungsspannung. Rechts die Hallsonde.

  • Versuch Fadenstrahlrohr Aufbau Röhre.jpg

  • Anschlüsse am Grundbrett

Beobachtungen

  • Bei Tageslicht ist der Elektronenstrahl kaum zu sehen.

  • Die Beschleunigungsspannung ist zu gering.

  • Der Elektronenstrahl ohne Magnetfeld.

  • Kleine Feldstärke oder große Spannung.

  • Mittlere Feldstärke oder mittlere Spannung.

  • Große Feldstärke oder kleine Spannung.

  • Die Elektronen bewegen sich auf einer Kreisbahn.
  • Der Radius des Kreises ist groß, wenn:
    • die Beschleunigungsspannung groß ist, oder
    • die Spulenstromstärke klein ist.
Messwerte

E-m-Bestimmung Messwerte.png

Auswertung

E-m-Bestimmung Skizze.jpg

Auf einen elektrischen Strom wirkt, senkrecht zu Strom- und Feldlinienrichtung, in einem Magnetfeld eine Kraft, die man Lorentzkraft nennt. Offensichtlich wirkt die Lorentzkraft auch auf die bewegten Elektronen außerhalb eines Kabels. Das Kabel ist also nicht zwingend notwendig.

Weil die Lorentzkraft immer senkrecht zur Bewegungsrichtung wirkt, wird das Elektron auf einer Kreisbahn gehalten. Wie ein Hammerwerfer beim Drehen des Hammers.

Die Richtung der Lorentzkraft bestimmt man mit der Drei-Finger-Regel der rechten Hand:

  • Daumen in technische Stromrichtung - Entgegen (!) der Bewegungsrichtung der Elektronen
  • Zeigefinger in Magnetfeldlinienrichtung
  • Mittelfinger zeigt die Kraftrichtung

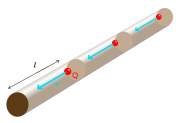
Die Stärke der Lorentzkraft berechnet sich mit:

[math]F_L=\mu_0 \, H \, I\, l[/math]

Die Stromstärke muss man mit der Ladung und der Geschwindigkeit des Elektrons ausdrücken:

Lorentzkraft Zusammenhang Strom bewegte Ladung.png
[math] \begin{array}{rcll} F_L &=& \mu_0 \, H \, \frac{Q}{t} \, l & \qquad \text{Stromstärke ist Ladung pro Zeit}\\ &=& \mu_0 \, H \, Q \, \frac{l}{t} & \qquad \text{Länge pro Zeit ist die Geschwindigkeit}\\ &=& \mu_0 \, H \, e \, v & \qquad \text{die Ladung beträgt hier } e\\ \end{array}[/math]

Damit hat man ein wichtiges Zwischenergebnis gefunden:

Lorentzkraft auf eine senkrecht zu einem Magnetfeld bewegte elektrische Ladung:

[math]F_L = \mu_0 \, H \, Q \, v[/math]

Der Zusammenhang zwischen wirkender Kraft und den Abmessungen der Kreisbahn ergibt sich aus der Mechanik der Kreisbewegungen. Die Zentripetalkraft beträgt:

[math]F_Z=\frac{m\,v^2}{r}[/math]

In diesem Fall ist die Lorentzkraft ja gerade die Zentripetalkraft, also kann man die wirkende Kraft auf zwei verschiedene Arten berechnen:

[math]\mu_0 \, H \, e \, v =F= \frac{m\,v^2}{r}[/math]

Um die Größe des Kreises zu bestimmen, kann man nach dem Radius auflösen:
[math]r=\frac{m\,v^2 }{e\,\mu_0\, H \,v} =\frac{m\,v }{e\,\mu_0\, H} \quad \Rightarrow \quad r \sim \frac{v}{H}[/math]

Der Radius ist also proportional zur Geschwindigkeit und antiproportional zur Feldstärke. Das erklärt die Zunahme des Radius mit der Beschleunigungsspannung und die Abnahme des Radius mit ansteigender Stromstärke.

Versuch: Elektronenstrahlen schräg zum Magnetfeld

Beobachtung

  • Elektronenstrahl senkrecht zur Feldlinienrichtung

  • Strahl leicht gekippt

  • Strahl stärker gekippt

  • ... und mehr

  • Hier erkennt man bereits den kleineren Radius

  • Aus dem Blickwinkel eine sehr verzerrte Spirale

  • Der zum Magnetfeld parallele Strahl

Aufbau der Bildröhre eines Fernsehers

Die Fernsehröhre ist eine besondere Form der Braun’schen Röhre [1], 1897 von Ferdinand Braun entwickelt. Anstatt mit geladenen Ablenkplatten erfolgt die Ablenkung des Elektronenstrahles hier mit Hilfe elektrischer Spulen (Magnetische Ablenkung). Die Technik wird auch bei Computerbildschirmen verwendet.

Mehr dazu... [2]

Versuch

In einem Versuch wiesen wir diese Funktionsweise an einem Röhrenmonitor nach.

Führt man an diesen einen Magneten, ergeben sich Bildverschiebungen und Farbstörungen [3], die erst mit der "Entmagnetisierung" wieder verschwinden.

Das Elektronenmikroskop

Teilchenbeschleuniger und Teilchendetektoren

-Ringbeschleuniger -Blasenkammer -radioaktive Strahlen im Magnetfeld


Polarlichter und die magnetische Flasche

Versuch: Elektronen im inhomogenen Feld

Beobachtung

  • Der Elektrononstrahl läuft parallel zu den Feldlinien des Stabmagneten direkt auf den Südpol zu und wird gebündelt.

  • Der Magnetpol wurde nach unten verschoben.

  • ... und noch weiter nach unten.

  • Die Position der Magnete ändert das Ergebnis sehr stark.

  • Ein zweiter Magnet reflektiert den Strahl zurück.

  • Es entsteht eine "magnetische Flasche"

  • Eine Simulation der Teilchenbewegung im Magnetfeld der Erde zum Herunterladen. (Matthias Borchert)

Das Massenspektroskop ; Geschwindigkeitsfilter ; Wienscher Filter

Links


Von „http://schulphysikwiki.de/index.php?title=Ladungen_im_magnetischen_Feld_(Lorentzkraft)&oldid=13469“