Energie und Impuls (Potential und Kraftverlauf) einer mechanischen Schwingung: Unterschied zwischen den Versionen

Version vom 14. November 2011, 13:21 Uhr

Die Wege von Impuls und Energie

Ein Körper kann nie alleine schwingen. Er braucht einen Partner.

Selbst bei einem Federpendel, das z.B. an einer Wand befestigt ist (bei dem es folglich so aussieht, als würde nur ein Körper schwingen), schwingt immer ein anderer Körper, in diesem Fall die Erde, mit.

Die zwei Körper schwingen dabei mit einem feststehenden gemeinsamen Schwerpunkt.

Bei dem oben genannten Beispiel wäre der gemeinsame Schwerpunkt, da die Erde ja eine viel größere Masse hat als der Rest des Federpendel, nahezu identisch mit dem der Erde, wodurch es dem Betrachter so erscheint, als würde nur das Federpendel schwingen.

Zwei Körper schwingen

Ein Vergleich der Darstellungen mit Kräften und mit dem Impulsfluss bei einer Feder unter Zugspannung. (Die positive Impulsrichtung ist nach rechts.)

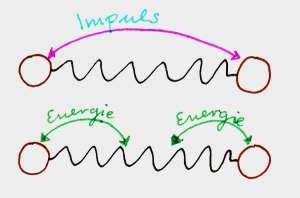
Während einer Schwingung fließt die Energie doppelt so schnell zwischen den Körpern (Bewegungsenergie) und der Feder (potentielle Energie) hin und her, wie der Impuls zwischen den zwei Körpern.

Der Impuls- und Energiefluss.

Dies lässt sich gut an dem folgenden Bild verdeutlichen.

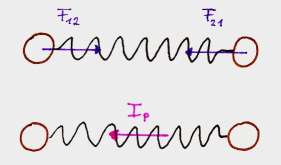
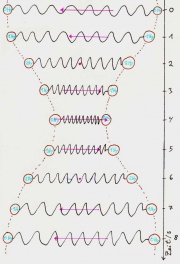
Wenn die Feder vollstängig auseinandergezogen oder zusammengedrückt ist, enthält sie alle Energie des Systems (Beide Körper bewegen sich an genau diesem Punkt nicht). Ist sie entspannt, so enthält sie gar keine. Beim folgenden Bild wäre die Energie also im ersten Abschnitt in der Feder, im dritten vollständig in den Körpern, im fünften wieder in der Feder, im siebten in den Körpern un im letzten wieder in der Feder. Sie hat sich also zwei mal zwischen Feder und den Körpern hin und her bewegt.

Der Impuls wandert hingegen nur einmal zwischen den Körpern hin und her:
Im ersten Abschnitt haben beide Körper keinen Impuls, im dritten hat der linke Körper den maximalen Impuls, während der rechte den maximalen negativen Impuls hat, im fünften haben beide wieder gar keinen, im siebten hat der rechte den positiven und der linke den negativen Impuls und am Ende haben beide wieder gar keinen.

Der Impulsfluss während einer Schwingung.

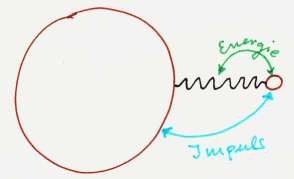
Die Erde als Schwingungspartner

Ist die Erde (oder ein ähnlich großer Körper) einer der zwei schwingenden Körper und der andere Körper ist erheblich kleiner, so nimmt die Erde zwar Impuls auf, aber kaum Energie.

Die Erde als Schwingungspartner.

Rechnung:

[math]E_{Erde}={1 \over 2} MV^2 = {P^2 \over 2M} \qquad .[/math] da [math] V = {P \over M} [/math]

[math]E_m={1 \over 2} mv^2 = {p^2 \over 2m} \qquad .[/math] da [math] v = {p \over m} [/math]

Weil aber der Impuls beider Körper gleich ist [math]( P=p )[/math], folgt:

[math]\Rightarrow E_{Erde}\lt\ltE_m[/math]

Grafische Darstellungen

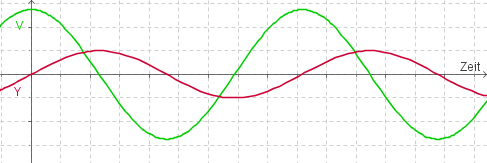
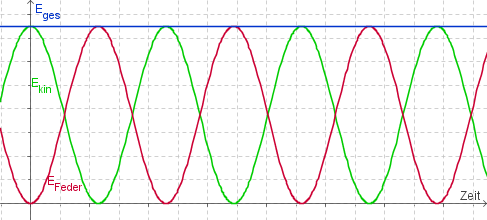
in Abhängigkeit von der Zeit

Die Geschwindigkeit und die Elongation hängen über die kinetische Energie miteinander zusammen.

Die Elongation Y und die Geschwindigkeit V in Abhängigkeit der Zeit.

Die Energie der Feder E_Feder, die Bewegungsenergie des schwingenden Körpers E_kin und die Gesamtenergie E_ges in Abhängigkeit der Zeit.

Die Gesamtenergie ist konstant.

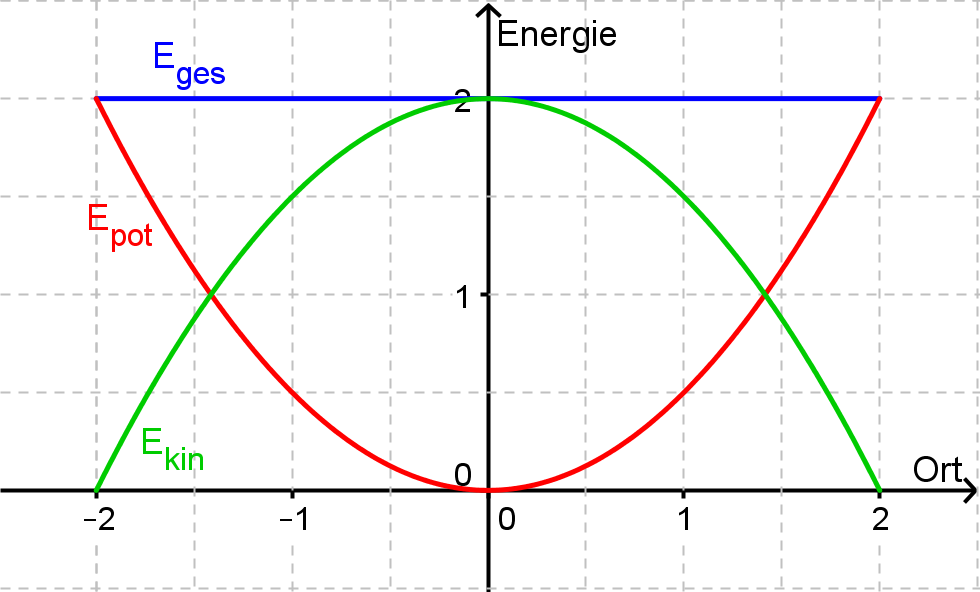
in Abhängigkeit vom Ort

In Abhängigkeit von der Elongation steigt die potentielle Energie quadratisch, während die kinetische Energie quadratisch abnimmt.

Die Gesamtenergie ist die Addition beider Energien, bleibt also konstant.

Die Energieformen eines (horizontalen) Federpendels in Abhängigkeit vom Ort.

Formeln

Die Gesamtenergie lässt sich auf zwei Arten bestimmen:

Über die kinetische Energie:

[math] E = {1 \over 2}mv^2[/math]
mit [math]v=\hat v = \hat y \omega[/math]

 [math]\Rightarrow E ={m \over 2}\omega^2 \hat y^2[/math]

Über die Spannenergie:

[math] E = {1 \over 2}Ds^2[/math]
mit [math]s = \hat y [/math]

 [math]\Rightarrow E ={D \over 2} \hat y^2[/math]

Beide Formeln sind gleichwertig.
Die Energie ist proportional zum Quadrat der Frequenz und zum Quadrat der Amplitude.