Energie und Impuls (Potential und Kraftverlauf) einer mechanischen Schwingung: Unterschied zwischen den Versionen
K |
(→Grafische Darstellungen) |
||
| Zeile 62: | Zeile 62: | ||
==Grafische Darstellungen== | ==Grafische Darstellungen== | ||
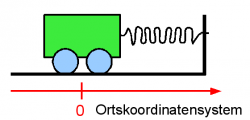
[[Bild:Schwingungen_Wagen_an_Feder.png|thumb|250px]] | [[Bild:Schwingungen_Wagen_an_Feder.png|thumb|250px]] | ||
| − | Die Diagramme sind für eine einfache harmonische Feder-Schwingung eines Wagens berechnet worden. Sie sehen aber für nichtharmonische Schwingungen ähnlich aus. | + | Die Diagramme sind für eine einfache [[Woran man eine harmonische Schwingung erkennt (Vier gleichwertige Kriterien)|harmonische]] Feder-Schwingung eines Wagens berechnet worden. Sie sehen aber für nichtharmonische Schwingungen ähnlich aus. |
| + | |||
| + | Da der Wagen zusammen mit der Erde schwingt, kann man seinen Schwingungspartner als ruhend betrachten. Alle Diagramme beschreiben die Eigenschaften des Wagens aus der Sicht eines auf der Erde ruhenden Betrachters. | ||
| + | |||
| + | |||
===in Abhängigkeit von der Zeit=== | ===in Abhängigkeit von der Zeit=== | ||
| − | Hier kann man sehen, wie | + | Hier kann man sehen, wie die Elongation und die Geschwindigkeit (und wegen <math>p=m\, v</math> auch der Impuls) sich mit der Zeit verändern. |
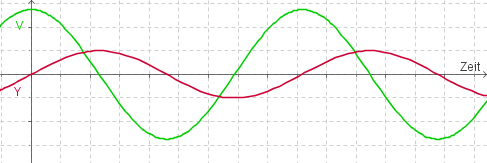
[[Bild:Schwingung_Y_V_Federschwingung.png|framed|none|Die Elongation Y und die Geschwindigkeit V in Abhängigkeit der Zeit.]] | [[Bild:Schwingung_Y_V_Federschwingung.png|framed|none|Die Elongation Y und die Geschwindigkeit V in Abhängigkeit der Zeit.]] | ||
| − | Die Bewegungsenergie hängt direkt mit der Geschwindigkeit zusammen. Die Gesamtenergie bleibt konstant. | + | Die Bewegungsenergie hängt über <math>E_{kin}=1/2 \, m v^2</math> direkt mit der Geschwindigkeit zusammen. Man erkennt auch gut, dass die Energie in jeder Periode zweimal die Form wechselt. Die Gesamtenergie bleibt konstant. |
| + | |||
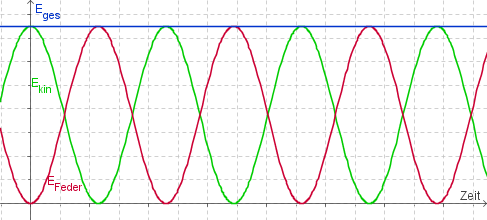
[[Bild:Schwingung_E_kin_E_pot_Federschwingung.png|framed|none|Die Energie der Feder E<sub>Feder</sub>, die Bewegungsenergie des schwingenden Körpers E<sub>kin</sub> und die Gesamtenergie E<sub>ges</sub> in Abhängigkeit der Zeit.]] | [[Bild:Schwingung_E_kin_E_pot_Federschwingung.png|framed|none|Die Energie der Feder E<sub>Feder</sub>, die Bewegungsenergie des schwingenden Körpers E<sub>kin</sub> und die Gesamtenergie E<sub>ges</sub> in Abhängigkeit der Zeit.]] | ||
Version vom 24. November 2011, 10:37 Uhr
Inhaltsverzeichnis
Versuche und Beispiele
Versuch: Ein Pendel auf einem Skateboard
Beobachtung
Kann man sich hier als Video anschauen.
Versuch: Schwingende Wagen
Beobachtung
Kann man sich hier als Video anschauen.
Animation
Zur Vereinfachung der Situation ist bei dieser Animation die Feder jeweils im Kugelmittelpunkt befestigt. Bei einer realen Situation würde sich die Befestigung natürlich an den Rand der Kugel verschieben.
Man kann die Masse der rechten Kugel und die Gesamtenergie der Schwingung einstellen.
Zur Steuerung läßt sich die Animation in Zeilupe ablaufen oder anhalten. Dann läßt sich die Zeit auch mit dem Schieberegler verstellen.
Die Geogebradatei kann man hier herunterladen.
Die Wege von Impuls und Energie
Ein Körper kann nie alleine schwingen. Er braucht einen Partner.
Selbst bei einem Federpendel, das z.B. an einer Wand befestigt ist (bei dem es folglich so aussieht, als würde nur ein Körper schwingen), schwingt immer ein anderer Körper, in diesem Fall die Erde, mit.
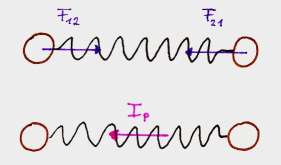
Die Erklärung liefert die Impulserhaltung: Die beiden Körper schwingen mit einem feststehenden gemeinsamen Schwerpunkt. Die Summe der Impulse ist, im Schwerpunktsystem, immer Null. Beide Körper enthalten zu jedem Zeitpunkt die gleiche Impulsmenge, allerdings mit entgegengesetzter Richtung.
Bei dem an der Wand befestigten Federpendel wäre der gemeinsame Schwerpunkt, da die Erde ja eine viel größere Masse hat als der Rest des Federpendel, nahezu identisch mit dem der Erde, wodurch es dem Betrachter so erscheint, als würde nur das Federpendel schwingen.
Zwei Körper schwingen
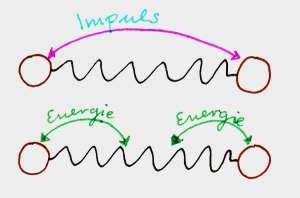
Während einer Schwingung fließt die Energie doppelt so schnell zwischen den Körpern (Bewegungsenergie) und der Feder (potentielle Energie) hin und her, wie der Impuls zwischen den zwei Körpern.
Dies lässt sich gut an dem folgenden Bild verdeutlichen.
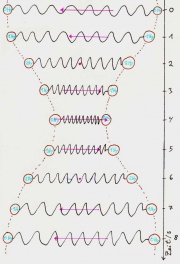
Wenn die Feder vollständig auseinandergezogen (Nr.0) oder zusammengedrückt (Nr.4) ist, enthält sie alle Energie des Systems (Beide Körper bewegen sich an genau diesem Punkt nicht). Ist sie entspannt (Nr.2 und Nr.6), so enthält sie gar keine. Die Energie hat sich also während einer Periode zwei mal zwischen Feder und den Körpern hin und her bewegt.
Der Impuls wandert hingegen nur einmal zwischen den Körpern hin und her: Sind die Kugeln in der Ruhelage (Nr.3 und Nr.6), so ist der Impuls maximal oder minimal.
Der (nach rechts gerichtete) Impuls ist also beim Durchgang durch die Ruhelage einmal in der linken Kugel (Nr.3) und einmal in der rechten Kugel (Nr.6).
Die Erde als Schwingungspartner
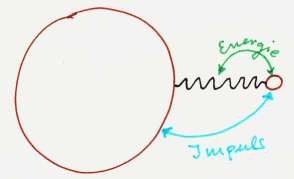
Ist die Erde (oder ein ähnlich großer Körper) einer der zwei schwingenden Körper und der andere Körper ist erheblich kleiner, so nimmt die Erde zwar Impuls auf, aber kaum Energie.
Rechnung:
[math]E_{Erde}={1 \over 2} MV^2 = {P^2 \over 2M} \qquad .[/math] da [math] V = {P \over M} [/math]
[math]E_m={1 \over 2} mv^2 = {p^2 \over 2m} \qquad .[/math] da [math] v = {p \over m} [/math]
Weil aber der Impuls beider Körper gleich ist [math]( P=p )[/math], folgt:
[math]\Rightarrow E_{Erde}\lt\ltE_m[/math]
Grafische Darstellungen
Die Diagramme sind für eine einfache harmonische Feder-Schwingung eines Wagens berechnet worden. Sie sehen aber für nichtharmonische Schwingungen ähnlich aus.
Da der Wagen zusammen mit der Erde schwingt, kann man seinen Schwingungspartner als ruhend betrachten. Alle Diagramme beschreiben die Eigenschaften des Wagens aus der Sicht eines auf der Erde ruhenden Betrachters.
in Abhängigkeit von der Zeit
Hier kann man sehen, wie die Elongation und die Geschwindigkeit (und wegen [math]p=m\, v[/math] auch der Impuls) sich mit der Zeit verändern.
Die Bewegungsenergie hängt über [math]E_{kin}=1/2 \, m v^2[/math] direkt mit der Geschwindigkeit zusammen. Man erkennt auch gut, dass die Energie in jeder Periode zweimal die Form wechselt. Die Gesamtenergie bleibt konstant.
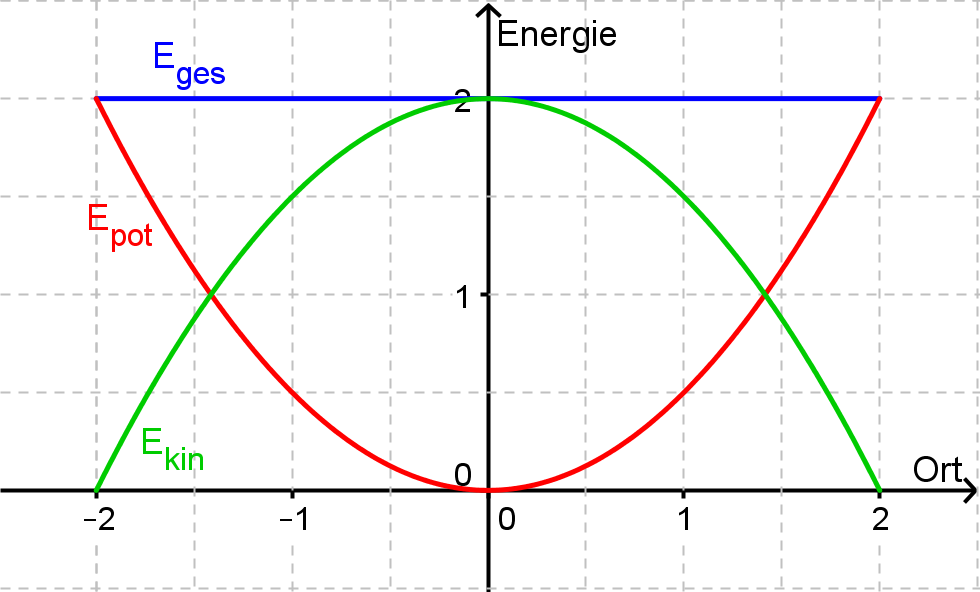
in Abhängigkeit vom Ort
In Abhängigkeit von der Elongation steigt die potentielle Energie quadratisch, während die kinetische Energie quadratisch abnimmt.
Die Gesamtenergie ist die Addition beider Energien, bleibt also konstant.