Der Kondensator: Unterschied zwischen den Versionen
(→Links) |
(→Die U-Q-Kennlinie und die Kapazität eines Kondensators) |
||
| Zeile 46: | Zeile 46: | ||
Beim Laden eines Kondensators nimmt nicht nur die Ladungsmenge auf den Platten zu, sondern auch die Spannung zwischen den Platten. Das entspricht der Zunahme der Druckdifferenz beim Aufpumpen eines Reifens oder Luftballons. | Beim Laden eines Kondensators nimmt nicht nur die Ladungsmenge auf den Platten zu, sondern auch die Spannung zwischen den Platten. Das entspricht der Zunahme der Druckdifferenz beim Aufpumpen eines Reifens oder Luftballons. | ||
| − | Trägt man die Spannung über der Ladung einer Platte auf, so erhält man eine U-Q-Kennlinie. | + | Trägt man die Spannung über der Ladung einer Platte auf, so erhält man eine U-Q-Kennlinie (U(Q)-Diagramm): |
| + | |||
| + | Eine anschauliche Vorstellung davon bekommt man beim Aufblasen eines Reifens oder eines Luftballons: | ||
| + | |||
| + | Vergleich zwischen Fahrrad- und Autoreifen. | ||
| + | |||
| + | Je dehnbarer der Reifen oder der Ballon, desto flacher steigt die Druckkurve an. Die Steilheit der Druckkurve ist also ein Maß für die Festigkeit der Hülle. | ||
| + | |||
| + | ====Die Kapazität des idealen Kondensators==== | ||
| + | Bei einem idealen, oder besser ''idealisierten Kondensator'', ist die Spannung proportional zur gespeicherten Ladung: | ||
| + | :<math>U \sim Q \qquad \Leftrightarrow \qquad U = k \, Q</math> mit einer Proportionalitätskonstante k. | ||
| + | Diese Konstante könnte man in hinsicht auf den mechanischen Vergleich die Festigkeit nennen. Weil man sich aber bei Kondensatoren vor allem dafür interessiert möglichst viel Ladung bei kleiner Spannung zu speichern, betrachtet man lieber die "Weichheit" des Kondensators, also wieviel Ladung pro Spannung hineinpasst: | ||
| + | <math>\frac{U}{Q}=C \qquad \Leftrightarrow \qquad U = \frac{1}{C}\, Q</math> | ||
| + | Der konstante Quotient aus Ladung und Spannung heißt "Kapazität". | ||
| + | Besser wäre "relative Kapazität, denn sie gibt an, wieviel Coulomb Ladung pro Volt Spannung gespeichert werden können. | ||
==Links== | ==Links== | ||
*Wikipedia: [http://de.wikipedia.org/wiki/Kondensator_%28Elektrotechnik%29 Kondensator (Elektrotechnik)] | *Wikipedia: [http://de.wikipedia.org/wiki/Kondensator_%28Elektrotechnik%29 Kondensator (Elektrotechnik)] | ||
*Messung des [http://www.sn.schule.de/~physik/ballon/ballon7.php p(V)-Diagramms eines Luftballons] (Mario Brauer, Sächsischer Bildungsserver ) | *Messung des [http://www.sn.schule.de/~physik/ballon/ballon7.php p(V)-Diagramms eines Luftballons] (Mario Brauer, Sächsischer Bildungsserver ) | ||
Version vom 20. Juni 2012, 10:08 Uhr
Ein einfacher Platten-Kondensator besteht aus zwei zueinander parallelen elektrisch leitenden Platten. Zwischen ihnen befindet sich häufig nicht nur Luft, sondern andere Materialien, die man dann "Dielektrikum" nennt. Die Platten kann man elektrisch laden.
Zwei Aspekte sind für uns interessant:
- Das homogene Feld des Kondensators
Dieser Aspekt spielt bei vielen theoretischen Überlegungen eine große Rolle. Für das magnetische Feld betrachtet man das Feld einer Spule.
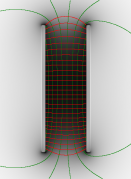
Ist der Plattenabstand gegenüber der Plattengröße klein, so kann man annehmen, dass sich nur zwischen den Platten ein elektrisches Feld befindet und ausserhalb keines. Dieses Feld ist dann in Richtung und Stärke homogen.
So kann man den Energiegehalt des elektrischen Feldes untersuchen und auch Aussagen über das Verhalten von Materie im elektrischen Feld machen.
- Der Kondensator als Ladungs- und Energiespeicher
In elektrischen Schaltungen befinden sich häufig Kondensatoren verschiedenster Bauart. Sie haben die Aufgabe Ladung und damit auch zu speichern. Man findet sie z.B. in Fahrradstandlichtern oder in elektrischen Schwingkreisen aller Art. In der Wechselstromtechnik spielen sie eine große Rolle, ähnlich wie ein ohmscher Widerstand.
Dieser Platten-Kondensator wurde mit einer Spannung von 3,5kV geladen.
Im Feldlinienbild sieht man die Inhomogenität des el. Feldes an den Rändern des Kondensators
Verschiedene Bauformen von Kondensatoren.
Inhaltsverzeichnis
Der Kondensator als Ladungs- und Energiespeicher
Vergleich mit einem aufgepumpten Fahrradreifen
| Fahrradreifen | Kondensator |
|---|---|
| speichert Luft | speichert el. Ladung |
| Druckenergie der Luft | el. Energie des Feldes |
| Luftdruck | el. Potential |
| Druckunterschied | Spannung |
Die U-Q-Kennlinie und die Kapazität eines Kondensators
Beim Laden eines Kondensators nimmt nicht nur die Ladungsmenge auf den Platten zu, sondern auch die Spannung zwischen den Platten. Das entspricht der Zunahme der Druckdifferenz beim Aufpumpen eines Reifens oder Luftballons.
Trägt man die Spannung über der Ladung einer Platte auf, so erhält man eine U-Q-Kennlinie (U(Q)-Diagramm):
Eine anschauliche Vorstellung davon bekommt man beim Aufblasen eines Reifens oder eines Luftballons:
Vergleich zwischen Fahrrad- und Autoreifen.
Je dehnbarer der Reifen oder der Ballon, desto flacher steigt die Druckkurve an. Die Steilheit der Druckkurve ist also ein Maß für die Festigkeit der Hülle.
Die Kapazität des idealen Kondensators
Bei einem idealen, oder besser idealisierten Kondensator, ist die Spannung proportional zur gespeicherten Ladung:
- [math]U \sim Q \qquad \Leftrightarrow \qquad U = k \, Q[/math] mit einer Proportionalitätskonstante k.
Diese Konstante könnte man in hinsicht auf den mechanischen Vergleich die Festigkeit nennen. Weil man sich aber bei Kondensatoren vor allem dafür interessiert möglichst viel Ladung bei kleiner Spannung zu speichern, betrachtet man lieber die "Weichheit" des Kondensators, also wieviel Ladung pro Spannung hineinpasst:
[math]\frac{U}{Q}=C \qquad \Leftrightarrow \qquad U = \frac{1}{C}\, Q[/math]
Der konstante Quotient aus Ladung und Spannung heißt "Kapazität".
Besser wäre "relative Kapazität, denn sie gibt an, wieviel Coulomb Ladung pro Volt Spannung gespeichert werden können.
Links
- Wikipedia: Kondensator (Elektrotechnik)
- Messung des p(V)-Diagramms eines Luftballons (Mario Brauer, Sächsischer Bildungsserver )
