Der Kondensator

(Kursstufe > Das elektrische Feld)

Ein einfacher Platten-Kondensator besteht aus zwei zueinander parallelen elektrisch leitenden Platten. Zwischen ihnen befindet sich häufig nicht nur Luft, sondern andere Materialien, die man dann "Dielektrikum" nennt. Die Platten kann man elektrisch laden.

Zwei Aspekte sind für uns interessant:

Das homogene Feld des Kondensators

Dieser Aspekt spielt bei vielen theoretischen Überlegungen eine große Rolle. Für das magnetische Feld betrachtet man das Feld einer Spule.

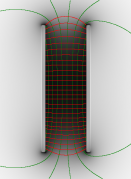
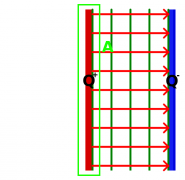
Ist der Plattenabstand gegenüber der Plattengröße klein, so kann man annehmen, dass sich nur zwischen den Platten ein elektrisches Feld befindet und außerhalb keines. Dieses Feld ist dann in Richtung und Stärke homogen.

So kann man den Energiegehalt des elektrischen Feldes untersuchen und auch Aussagen über das Verhalten von Materie im elektrischen Feld machen.

Der Kondensator als Ladungs- und Energiespeicher

In elektrischen Schaltungen befinden sich häufig Kondensatoren verschiedenster Bauart. Sie haben die Aufgabe Ladung und damit auch Energie zu speichern. Man findet sie z.B. in Fahrradstandlichtern oder in elektrischen Schwingkreisen aller Art. In der Wechselstromtechnik spielen sie eine große Rolle, ähnlich wie ein ohmscher Widerstand.

• 

  Dieser Platten-Kondensator wurde mit einer Spannung von 3,5kV geladen.

• 

  Im Feldlinienbild sieht man die Inhomogenität des el. Feldes an den Rändern des Kondensators

• 

  Verschiedene Bauformen von Kondensatoren.

• 

  Mainboard eines Smartphones: Mit Kondensatoren kann man Beschleunigungen messen.

Der Kondensator als Ladungs- und Energiespeicher

Was passiert, wenn man den Hahn öffnet?

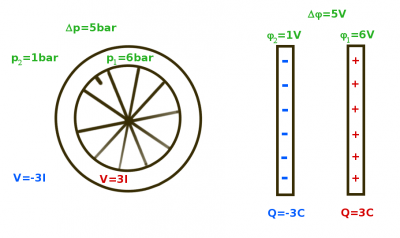
Einen geladenen Kondensator kann man mit einem aufgepumpten Fahrradreifen vergleichen:

Fahrradreifen Kondensator speichert Luft speichert el. Ladung Druckenergie der Luft el. Energie des Feldes Luftdruck el. Potential Druckunterschied Spannung

Der Reifen wurde mit 3 Litern Umgebungsluft gefüllt. Beim Kondensator wurden 3 Coulomb Ladung von der linken auf die rechte Platte verschoben.

Mechanische Messung des Energiegehalts

Aufbau

Der Versuchsaufbau

Der Doppelschichtkondensator

Ein Doppelschichtkondensator (5,5V/1F) wird geladen, indem er ca. eine halbe Minute mit einer 4,5V-Flachbatterie verbunden wird. (Dabei muss man auf die Polung achten.) Damit kann man einen Elektromotor betreiben, der ein kleines Gewicht von 10g Masse hochhebt.

Für eine quantitative Messung läßt man das Gewicht jeweils einen Meter hochziehen, läßt es dann wieder nach unten fallen, und zählt wie oft der Kondensator "das schafft".

Beobachtung

Der geladene Kondensator kann das Gewicht ungefähr 31 mal einen Meter nach oben ziehen.

Auswertung

Die im Kondensator gespeicherte Energie wird genutzt, um die Lageenergie des Gewichtes zu erhöhen, welches insgesamt 31 Meter hochgehoben wurde:

[math]E_{el} = W = F\, s = m\,g\,h = 0{,}010\,\rm kg \cdot 10\,\rm \frac{N}{kg}\cdot 31\,\rm m = 0{,}1\, N \cdot 31\,\rm m = 3{,}1\,\rm Nm = 3{,}1\,\rm J [/math]

Im Vergleich zu Batterien oder Akkus ist das nicht besonders viel, so speichert ein Handy-Akku (3,85V/2800mAh) schon fast 40000J, aber für einen Kondensator ist das schon eine eher große Energiemenge. Im Praktikum wird die Energiemenge genauer gemessen.

Die U-Q-Kennlinie und die Kapazität eines Kondensators

Mit diesem Versuchsaufbau kann man die U-Q-Kennlinie des Kondensators messen. (Die Rasierklinge benötigt man nicht.)

Stark idealisierter Zusammenhang zwischen Druck und Volumen von Reifen.

Beim Laden eines Kondensators nimmt nicht nur die Ladungsmenge auf den Platten zu, sondern auch die Spannung zwischen den Platten. Das entspricht der Zunahme der Druckdifferenz beim Aufpumpen eines Reifens oder Luftballons.

Trägt man die Spannung über der Ladung einer Platte auf, so erhält man eine U-Q-Kennlinie (U(Q)-Diagramm).

Eine anschauliche Vorstellung davon bekommt man beim Aufblasen eines Reifens oder eines Luftballons.

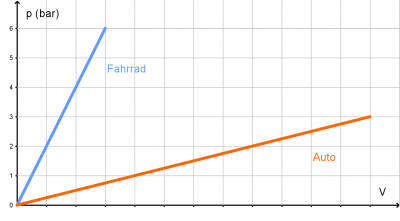
Wie unterscheidet sich wohl der Verlauf des p(V)-Diagramms bei einem Autoreifen von einem Diagramm eines Fahrradreifens?

Pumpt man einen Fahrradreifen auf, so steigt der Luftdruck im Reifen schnell an. Man kann die meisten Reifen bis mindestens 6bar aufpumpen bevor sie platzen, aber es passt nicht viel Luft hinein. Die p(V)-Kennlinie ist relativ steil.

Bei einem Autoreifen steigt der Druck nicht so schnell mit dem zugeführten Luftvolumen an. Die meisten Autoreifen soll man nur bis ca. 3bar aufpumpen, aber es passt viel mehr Luft in den Autoreifen als in den Fahrradreifen. Die p(V)-Kennlinie ist relativ flach.

Je dehnbarer der Reifen oder der Ballon, desto flacher steigt die Druckkurve an. Die Steilheit der Druckkurve ist also ein Maß für die Festigkeit der Hülle.

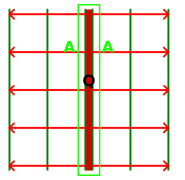
Animation eines veränderbaren Plattenkondensators

Der Plattenkondensator kann mit einer Spannungsquelle verbunden und wieder von ihr getrennt werden.

Bei verbundener Spannungsquelle kann man mit dem Schieberegler die Spannung einstellen.

Weiterhin ist der Plattenabstand, die Plattenfläche und das Dielektrikum zwischen den Platten einstellbar.

Die Animation gestattet es viele Eigenschaften des Kondensators nachzuvollziehen und greift an dieser Stelle auf noch folgende Themen vor.

Der ideale Kondensator

Bei diesem realen Plattenkondensator ist das elektrische Feld zwischen den Platten nicht ganz homogen.

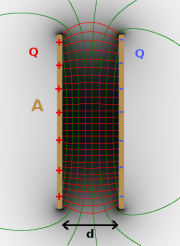
Wir betrachten einen idealen Plattenkondensator, bei dem sich ausschließlich zwischen den Platten ein homogenes Feld befindet, mit folgenden Eigenschaften:

• Plattenfläche A
• Plattenabstand d
• Ladung Q
• Spannung U

Der Zusammenhang zwischen Ladung und Feldstärke

Die Feldstärke ist proportional zur Ladung, wegen der Ladung als Quellenstärke des elektrischen Feldes:

[math]\epsilon_0 \, E \, A = Q[/math]

[math]\Rightarrow \quad E = \frac{1}{\epsilon_0}\,\frac{Q}{A}[/math]

Die Feldstärke ist proportional zur Flächenladungsdichte der Kondensatorplatten.

Der Zusammenhang zwischen Spannung und Feldstärke

Die Feldstärke ist gerade die räumliche Änderung ("Steigung") des Potentials:

[math]E = \frac{\Delta\varphi}{\Delta s} = \frac{U}{d}[/math]

Der Zusammenhang zwischen Ladung und Spannung: die Kapazität

Dieser Kondensator hat eine Kapazität von 0,5F. Bei 6V speichert er 3C Ladung und 9J Energie.

Die Feldstärke des Kondensators kann man mit Hilfe der Ladungsmenge oder aber mit der anliegenden Spannung bestimmen. Beides setzt man gleich:

[math]\frac{1}{\epsilon_0}\,\frac{Q}{A} = E = \frac{U}{d}[/math]

Jetzt kann man nach der Spannung auflösen:

[math]U = \frac{1}{\epsilon_0} \frac{d}{A}\, Q[/math]

Die Spannung ist also proportional zur gespeicherten Ladung

[math]U \sim Q \quad \Leftrightarrow \quad U = k \, Q[/math] mit einer Proportionalitätskonstante [math]k=\frac{1}{\epsilon_0} \frac{d}{A}[/math].

Diese Konstante k könnte man in Hinsicht auf den mechanischen Vergleich die Festigkeit nennen. Weil man sich aber bei Kondensatoren vor allem dafür interessiert möglichst viel Ladung bei kleiner Spannung zu speichern, betrachtet man lieber den Kehrwert von k, also die "Dehnbarkeit" des Kondensators, das heißt, wieviel Ladung pro Spannung hineinpasst:

Der konstante Quotient aus Ladung und Spannung eines idealen Kondensators heißt "Kapazität". Die Kapazität ist proportional zur Plattenfläche und antiproportional zum Plattenabstand. [math]C=\frac{Q}{U} \quad \Leftrightarrow \quad Q = C\, U \qquad \Leftrightarrow \quad U = \frac{1}{C}\, Q \qquad \rm{mit} \it \qquad C = \epsilon_0 \, \frac{A}{d} \quad \left[ C \, \right]= \rm 1\, Farad \;(F)[/math] Lädt man einen Kondensator einer Kapazität von [math]0{,}5\,\rm F[/math] bis zu einer Spannung von [math]6\,\rm V[/math] auf, so speichert er [math]3\,\rm C[/math] Ladung.

Besser wäre die Benennung als "relative Kapazität", denn sie gibt an, wieviel Coulomb Ladung pro Volt Spannung gespeichert werden können.

Energiegehalt

Lädt man einen Kondensator auf, so verschiebt man Ladungen. Dabei ist Energie nötig, denn man verschiebt die Ladungen von einem niedrigen zu einem hohen Potential, also "bergauf". Die gesamte benötigte Energie steckt danach im elektrischen Feld des Kondensators.

Der Ladevorgang entspricht dem Aufpumpen eines Fahrradreifens. Man pumpt Luft vom niedrigen Umgebungsdruck zum hohen Druck im Reifen. Die dazu benötigte Energie steckt im aufgepumpten Reifen und kommt aus dem Menschen, der die Pumpe zusammendrückt.
Am Anfang des Aufpumpens ist es "leicht" die Pumpe zusammenzudrücken, man benötigt wenig Energie um die in der Pumpe enthaltene Luftportion in den Reifen zu drücken. Ist der Reifen schon ziemlich "prall" geht es viel "schwerer", man benötigt also für den Transport der gleichen Luftmenge viel mehr Energie!

Genauso ist es beim Laden des Kondensators: Für die Verschiebung der Ladungsmenge [math]q[/math] bei einer Potentialdifferenz (Spannung) [math]\Delta \varphi = U[/math] braucht man die Energiemenge [math]E_{el} = W = q\, U[/math].
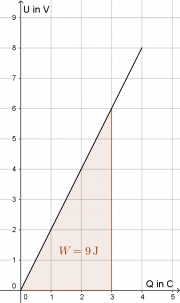
Während des Ladevorganges ist aber die Potentialdifferenz (Spannung) des Kondensators nicht konstant. Durch die größere Ladungsmenge auf den Platten steigt nämlich die Feldstärke und dadurch auch der Potentialunterschied an. In diesem Fall kann man die benötigte Energie als Fläche im Spannungs-Ladungs-Diagramm bestimmen.

Bezeichnet man die maximale Ladung auf einer Platte mit [math]Q[/math] und die maximale Spannung mit [math]U[/math], so folgt für die Fläche des rechtwinkligen Dreiecks:

[math]W=\frac{1}{2} \, Q \, U [/math]

Mit der Kapazität [math]C=\frac{Q}{U}[/math] ergibt sich [math]U = \frac{1}{C} \, Q[/math] und [math]Q = C \, U[/math], was man einsetzen kann:

Energiegehalt eines idealen Kondensators [math]W=\frac{1}{2} \, Q \, U = \frac{Q^2}{2\, C} = \frac{1}{2}\, C \, U^2 [/math]

Der Kondensator mit Dielektrikum

Versuch: Materialien im Kondensator

1. Aufbau: Erst Material, dann Laden

Ein Plattenkondensator mit statischem Voltmeter und Messverstärker zum Messen der Ladung.

Der Zwischenraum eines Plattenkondensators wird vollständig mit verschiedenen Materialien gefüllt, wobei der Plattenabstand konstant bleibt. Danach wird der Kondensator mit einer festen Spannung geladen und von der Spannungsquelle getrennt.

Mit Hilfe eines Messverstärkers wird die Ladung auf den Platten bestimmt.

Als Materialien kommen verschiedene Kunststoffe, Papier, Holz, Glas in Frage. Interessant ist auch das Einbringen von Ölen, flüssigem Wasser oder Eis, was allerdings schwerer zu realisieren ist.

1. Beobachtung

Der Kondensator speichert durch das Einbringen der Materialien mehr Ladung. Die Ladungsmenge hängt vom Material ab:

Spannung: 10 kV

Material Ladung
Luft      130nC
Holz      380nC
Glas      790nC

2. Aufbau: Erst Laden, dann Material

Ein Plattenkondensator mit statischem Voltmeter

Ein Plattenkondensator wird z.B. mit einer geriebenen Schallplatte oder mit einem Hochspannungsnetzgerät auf 10kV aufgeladen und dann von der Spannungsquelle getrennt.

Dann wird der Platten-Zwischenraum mit verschiedenen Materialien gefüllt: Kunststoff, Glas, Wasser,... (Der Zwischenraum wird nicht vollständig gefüllt, um die Materialien gut Einbringen zu können ohne den Plattenabstand zu verändern.)

Dabei wird die Spannung mit einem statischen Voltmeter gemessen.

2. Beobachtung

Beim Eintauchen der Gegenstände fällt die Spannung ab. Zieht man sie wieder heraus stellt sich annähernd die Ausgangsspannung wieder ein. Video des Versuchs. (Uni Würzburg)

Je nach Material fällt die Spannung unterschiedlich stark ab:

Material Spannung
Luft      10kV
Holz      4kV
Glas      5kV

Interpretation

Die in den Kondensator eingebrachten Materialien sind Isolatoren, deswegen fließen keine Ladungen und die Ladungsmenge auf den Platten bleibt konstant.

Weil der Kondensator mit Material bei geringerer Spannung die gleiche Ladung speichert, ist seine Kapazität größer geworden.

Die Feldstärke sollte wegen der gleichen Ladung pro Fläche eigentlich auch unverändert bleiben. Andererseits ist der Plattenabstand bei dem Versuch nicht geändert worden und die Potentialdifferenz hat durch das Einbringen des Materials abgenommen, also muss, wegen [math]E=\frac{U}{d}[/math], die Feldstärke abgenommen haben. Wie kann man das erklären?

Die Materialien verändern sich im elektrischen Feld. Die inneren Ladungen werden verschoben, das Material polarisiert oder influenziert. Solche polarisierbaren Isolatoren werden Dielektrika genannt. Durch die Polarisierung entstehen an den Rändern des Dielektrikums Polarisationsladungen [math]Q_{pol}[/math], die ein anderes Vorzeichen haben als die Ladungen auf den Platten. Zwei Argumentationen führen nun zum gleichen Ziel:

1. Die neue Gesamtladung [math]Q + Q_{pol}[/math] nimmt ab. Dadurch sinkt die Ladung pro Fläche und damit die Feldstärke:

[math]E = \frac{1}{\varepsilon_0}\frac{Q + Q_{pol}}{A}[/math]

Man kann auch sagen, dass die Quellenstärke und somit auch der Feldfluss abgenommen hat:

[math]\varepsilon_0\, E \, A = Q + Q_{pol} [/math]

2. Innerhalb des Dielektrikums baut sich ein ein elektrisches Gegenfeld auf, dessen Feldstärke antiparallel zur ursprünglichen Feldstärke ist. Das Gegenfeld verringert daher die Feldstärke.

Die Abnahme der Spannung (oder der Feldstärke), bzw. die Zunahme der Kapazität, gibt an, wie gut das jeweilige Material polarisiert werden kann.

Das Verhältnis aus Ausgangsspannung und Spannung mit Dielektrikum wird als "relative Permittivität" oder auch als "Dielektrizitätszahl" [math]\epsilon_r[/math] bezeichnet. Bei einer relativen Permittivität von [math]\epsilon_r=3[/math] sinkt bei gleicher Ladung die Feldstärke auf 1/3 des Ausgangswertes, ebenso sinken die Spannung zwischen den Platten und die effektive Gesamtladung auf 1/3 der Ausgangswerte.

1. Versuch:
Spannung: 10 kV
Material Ladung   relative Permittivität
Luft      130nC    1
Holz      380nC    2,9
Glas      790nC    6,1

2. Versuch:
Material Spannung relative Permittivität
Luft     10kV      1
Holz      4kV      2,5
Glas      5kV      2

Laut Literatur hat Holz eine relative Permittivität zwischen 2 und 3,5 ; Glas eine relative Permittivität von 6 bis 8. Bei unserer Messung war der Zwischenraum vom Glas auch nur zur Hälfte mit Glas gefüllt und das Spannungsmessgerät erlaubt bei niedrigeren Spannung keine genaue Messung, weshalb unsere Messung eher qualitativ ist.

• 

  Das elektrische Feld zwischen den Platten ist homogen.

• 

  Die Feldlinien und Feldflächen sind daher ganz regelmäßig.

• 
• 

  Ein Gegenstand im Kondensator wird vom Feld verändert und verändert das Feld.

• 

  Dieser isolierende Gegenstand wird durch Verschiebung der Elektronenhüllen polarisiert.

• 

  An den Oberflächen des Gegenstandes befinden sich Ladungen und es bildet sich innerhalb des Gegenstandes ein elektrisches Gegenfeld aus.

• 

  Die relative Permittivität dieses Dielektrikums beträgt [math]\epsilon_r=3[/math], denn die Feldstärke, die Spannung und die effektive Ladung sinken auf ein Drittel der Ausgangswerte ab.

Ein Kondensator mit Dielektrikum der relativen Permittivität [math]\epsilon_r[/math] hat eine um den Faktor [math]\epsilon_r[/math] größere Kapazität: [math] C = \epsilon_0 \, \epsilon_r \, \frac{A}{d}[/math] Beträgt die relative Permittivität [math]\epsilon_r =3[/math], so speichert er bei gleicher Spannung (gleicher Feldstärke) die dreifache Ladung, bzw. hat bei gleicher Ladung nur ein Drittel der Spannung (der Feldstärke).

Energiegehalt

Lädt man einen mit Dielektrikum gefüllten Kondensator auf, so benötigt man Energie, die sich in gleicher Weise berechnet wie bei einem mit Luft gefüllten Kondensator. Es gelten die gleichen Formeln. Der Unterschied ist lediglich, dass die U(Q)-Kennlinie flacher verläuft als ohne Dielektrikum, weil die Kapazität größer geworden ist:

[math]W= \frac{1}{2}\,Q\,U = \frac{1}{2}\,\frac{1}{C}\,Q = \frac{1}{2}\,C\,U^2[/math]

Vergleicht man den Energiegehalt eines Kondensators mit und ohne Dielektrikum, so kommt es darauf an, ob man dies bei gleicher Ladung oder bei gleicher Spannung tut.

Bei gleicher Ladung speichert ein Kondensator mit Dielektrikum nur den [math]\frac{1}{\epsilon_r}[/math]-ten Teil der Energie, denn die Spannung sinkt auf den [math]\frac{1}{\epsilon_r}[/math]-ten Teil:

[math]W = \frac{1}{2}\,Q\,\frac{1}{\epsilon_r}\,U[/math]

Man kann auch argumentieren, dass die Kapazität gestiegen ist:

[math]W= \frac{1}{2}\,\frac{1}{\epsilon_r\, C}\,Q [/math]

In der Praxis ist es aber relevanter bei gleicher Spannung zu vergleichen, denn man möchte die Energie bei möglichst kleiner Spannung speichern. Bei zu großen Spannungen werden Kondensatoren nämlich zerstört oder sie entladen sich.
Bei gleicher Spannung speichert ein Kondensator mit Dielektrikum [math]\epsilon_r[/math] mal soviel Energie, denn die Ladungsmenge ist um das [math]\epsilon_r[/math]-fache gestiegen:

[math]W = \frac{1}{2}\,\epsilon_r\,Q\,\,U[/math]

Man kann auch argumentieren, dass die Kapazität gestiegen ist:

[math]W= \frac{1}{2}\,\epsilon_r\, C\,U^2 [/math]

Dieser Kondensator hat eine Kapazität von 0,5F. Bei 6V speichert er 3C Ladung und 9J Energie.

Mit Dielektrikum ([math]\epsilon_r=3[/math]) hat der Kondensator eine Kapazität von 1,5F. Bei 6V speichert er 9C Ladung und 27J Energie. (Davon 9J im Feld und 18J im polarisierten Dielektrikum.) Bei 3C Ladung speichert er nur 3J Energie.

Bei gleicher Spannung speichert ein Kondensator durch das Dielektrikum [math]\epsilon_r[/math] mal soviel Energie. Der Anteil von [math]1/\epsilon_r[/math] wird im elektrischen Feld gespeichert, der Rest im polarisierten Dielektrikum.

Funktionen des Dielektrikums

Das Dielektrikum zwischen den Platten hat drei Funktionen: Es vergrößert die Kapazität des Kondensators. Es isoliert die Platten und erhöht die maximale Feldstärke (Durchschlagsfestigkeit) und damit die maximale Energiedichte. Es drückt die Platten auseinander, die vom elektrischen Feld zusammengezogen werden.

Die Kräfte auf die Kondensatorplatten

Das elektrische Feld zieht die beiden Platten zueinander. Die Stärke der Kräfte kann man am einfachsten über die Energiedichte des elektrischen Feldes berechnen.

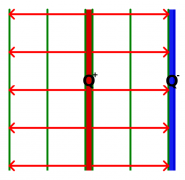
Alternativ berechnet man die Kräfte direkt über die Feldstärke und die Ladung. Dazu betrachten wir die rechte Platte als Probekörper im Feld der linken Platte. Die gesamte rechte Platte ist aber kein "kleiner" Probekörper mehr, durch die Anwesenheit der rechten Platte wird das Feld stark verändert. Wir müssen daher zunächst die Feldstärke [math]\tilde E[/math] der linken Platte ohne die Anwesenheit der rechten Platte berechnen. Wie immer wird dabei vorausgesetzt, das das Feld homogen ist, was für den Bereich "in der Nähe" der Platte gerechtfertigt ist.

• 

  Der Feldfluss geht bei einem Kondensator nur durch die Plattenfläche A.

• 

  Bei einer einzelnen Platte geht der Fluss durch die doppelte Plattenfläche.

• 

  Die rechte Platte als Probekörper im Feld der linken Platte.

Legt man um die linke Platte eine geschlossene Fläche, so hat sie die doppelte Fläche der Kondensatorplatte. Die Flächenladungsdichte hat sich halbiert. Der elektrische Fluss geht also durch die doppelte Fläche und damit halbiert sich die Feldstärke:

[math]\begin{array}{rrcll} & \epsilon_0\,\tilde E \cdot 2A &=& Q & | \, \mathopen: (\epsilon_0 \, 2\, A) \\ \Rightarrow & \tilde E &=& \frac{1}{2}\, \frac{1}{\epsilon_0}\, \frac{Q}{A}\\ & &=& \frac{1}{2}\,E \\ \end{array} [/math]

Die rechte Platte mit der Ladung [math]Q[/math] erfährt in diesem Feld der Stärke [math]\tilde E[/math] die Kraft

[math](*)\ F= Q\,\tilde E = \frac{1}{2}\,Q\,E [/math]

Die Kraft ist also nur halb so groß, als man vielleicht zunächst vermutet hätte.

Man kann das Ergebnis noch weiter umformen. Möchte man wissen, wie die Kraft von der Feldstärke abhängt, so setzt man [math]Q=\epsilon_0\,E\,A[/math] in [math](*)[/math] ein:

[math]F= \frac{1}{2}\, Q \,E = \frac{1}{2}\, \epsilon_0 \,A\,E^2 [/math]

Wegen dieses Zusammenhangs zwischen Kraft, Fläche und Feldstärke kann man dem elektrischen Feld eine Zugspannung längs der Feldlinien zuordnen und sie auch berechnen.

Es gibt auch einen Zusammenhang zwischen gespeicherter Energie und der Kraft. Man erhält ihn, indem man [math]E=\frac{U}{d}[/math] in [math](*)[/math] einsetzt:

[math]F= \frac{1}{2}\, Q \,E = \frac{1}{2}\, Q \,\frac{U}{d} = \frac{\frac{1}{2}\,Q\,U}{d} = \frac{W}{d}[/math]

Dieser Zusammenhang ist nicht überraschend, denn die Kraft ist, nach der "goldenen Regel der Mechanik", die räumliche Änderung der Energie.

Beschreibt man den Energiegehalt mit Hilfe der Ladung [math]W= \frac{1}{2}\, \frac{1}{C}\, Q^2 [/math] und setzt für die Kapazität [math]C= \epsilon_0\,\frac{A}{d}[/math] so erhält man den Zusammenhang zwischen Kraft und Ladung:

[math]F= \frac{Q^2}{2\,C\,d}= \frac{Q^2}{2\epsilon_0\,A} [/math]

Für den Zusammenhang zwischen Kraft und Spannung setzt man [math]W= \frac{1}{2}\, C \, U^2 [/math] ein:

[math]F= \frac{C\,U^2}{2\,d} = \frac{\epsilon_0\,A\,U^2}{2\,d^2} [/math]

Die Kraft auf die Platten eines idealen Kondensators ohne Dielektrikum beträgt: [math]F=\frac{1}{2} \, Q \, E = \frac{1}{2}\, \epsilon_0 \,A\,E^2 = \frac{Q^2}{2\epsilon_0\,A} = \frac{W}{d}[/math]

Beispielrechnung

Ein einfacher Plattenkondensator

• mit kreisförmigen Platten des Durchmessers 30cm,
• dem Plattenabstand 5mm,
• der auf 5kV geladen wird.

Nun möchte man gerne wissen,

• wie stark das elektrische Feld ist,
• wieviel Ladung auf den Platten ist,
• welche Kapazität der Kondensator hat,
• wieviel Energie gespeichert ist und
• welche Kraft auf die Platten wirkt.

Die Feldstärke ist die räumliche Änderungsrate des Potentials:

[math]E=\frac{U}{d} = \rm \frac{5000\, \rm V}{0,005\,\rm m} = 1000000\rm \frac{V}{m} [/math]

Die Ladungsmenge auf einer der Platten ist die Quellenstärke des Feldes:

[math] \begin{array}{rcl} Q &=& \epsilon_0 \, E \, A \\ &=& {8{,}854 \cdot 10^{-12} \rm \frac{As}{Vm} \cdot 1000000\rm \frac{V}{m} \cdot \,\pi \, (0{,}15}\, \rm m)^2 \\ &=& {8{,}854 \cdot 10^{-12} \rm \frac{As}{Vm} \cdot 1000000\rm \frac{V}{m} \, 0{,}0707}\,\rm m^2\\ &=& 6{,}25\cdot 10^{-7}\,\rm C = 626\,\rm nC \end{array}[/math]

Die Kapazität kann man direkt über die Eigenschaften des Kondensators berechnen oder als Ladung pro Spannung:

[math]C= \epsilon_0\,\frac{A}{d} = \frac{Q}{U} = \frac{625\cdot 10^{-9}\,\rm C}{5000\, \rm{V}} = 125\, \mu F[/math]

Die Energie kann man nun auf verschiedene Weise berechnen:

[math]E_{el}=\frac{1}{2} \, Q \, U = \frac{Q^2}{2\ C} = \frac{1}{2}\, C \, U^2 = 1{,}56\, \rm mJ[/math]

Zur Berechnung der Kraft auf die Platten hat man nun viele Möglichkeiten. Am einfachsten ist es über die gespeicherte Energie:

[math]F=\frac{1}{2} \, Q \, E = \frac{1}{2}\, \epsilon_0 \,A\,E^2 = \frac{Q^2}{2\epsilon_0\,A} = \frac{E_{el}}{d} = \frac{1{,}56 \cdot 10^{-3} \, \rm J}{5 \cdot 10^{-3} \, \rm m} = 0{,}31 \, \rm N[/math]

Ein Plattenkondensator mit Dielektrikum

Der gleiche Plattenkondensator enthält nun Glas als Dielektrikum:

• kreisförmigen Platten mit dem Durchmesser 30cm,
• dem Plattenabstand 5mm,
• auf 5kV geladen
• Glas hat die Permittivität [math]\epsilon_r = 6 [/math]
• und eine Durchschlagsfestigkeit von [math] E_{max} = 25\,\rm\frac{kV}{mm}[/math]

Nun möchte man gerne wissen:

• wie stark das elektrische Feld ist,
• wieviel Ladung auf den Platten ist,
• welche Kapazität der Kondensator hat,
• wieviel Energie gespeichert ist und
• welche Kraft auf die Platten wirkt

und zusätzlich:

• welche maximale Spannung man anlegen kann
• welche maximale Energiemenge gespeichert werden kann.

Die Feldstärke ist die räumliche Änderungsrate des Potentials und ist unverändert, weil wieder die gleiche Spannung beim gleichen Plattenabstand anliegt:

[math]E=\frac{U}{d} = \rm \frac{5000\, \rm V}{0,005\,\rm m} = 1000000\rm \frac{V}{m} [/math]

Zur Berechnung der Ladungsmenge muß man nun berücksichtigen, dass man 6 mal soviel Ladung verschieben muss, um die gleiche Feldstärke zu erreichen, da die Polarisationsladungen die effektive Gesamtladung und damit die Feldstärke verringern:

[math] \begin{array}{rcl} Q &=& \epsilon_0 \, \epsilon_r\, E \, A \\ &=& 6\cdot 6{,}25\cdot 10^{-7}\,\rm C = 6\cdot 626\,\rm nC = 3756\,\rm nC \end{array}[/math]

Die Kapazität des Kondensators ist nun 6 mal größer als vorher:

[math]C= \epsilon_0\,\epsilon_r\,\frac{A}{d} = \frac{Q}{U} = 6 \cdot 125\, \mu F = 750\, \mu F[/math]

Und auch die Energiemenge steigt auf das 6-fache:

[math]E_{el}=\frac{1}{2} \, Q \, U = \frac{Q^2}{2\ C} = \frac{1}{2}\, C \, U^2 = 6 \cdot 1{,}56\, \rm mJ = 9{,}36\, \rm mJ[/math]

Ebenso steigt die Anziehungskraft zwischen den Platten:

[math]F=\frac{1}{2} \, Q \, E = \frac{1}{2}\, \epsilon_0 \,A\,E^2 = \frac{Q^2}{2\epsilon_0\,A} = \frac{E_{el}}{d} = 6 \cdot \frac{1{,}56 \, \rm mJ}{5 \,\rm mm} = 6 \cdot 0{,}31 \, \rm N = 1{,}86 \, \rm N[/math]

Links

• Wikipedia: Kondensator (Elektrotechnik)
• Messung des p(V)-Diagramms eines Luftballons (Mario Brauer, Sächsischer Bildungsserver )
• Videos: Versuche mit dem Plattenkondensator Abstandsänderung bei konstanter Ladung, Materie im Feld
• Animation: Plattenkondensator (Download der deutschen JAVA Version) Abstand, Fläche und Dielektrikum sind wählbar. Es werden Energiegehalt, Kapazität, Feldstärke etc. angezeigt. (PhET Interactive Simulations der University of Colorado Boulder)
• Video: What is an Capacitor? youtube: "Dielectrics in capacitors | Circuits | Physics | Khan Academy" von "khanacademymedicine"