Selbstinduktion und die Induktivität einer Spule

(Kursstufe > Elektro-Magnetismus)

Ändert sich bei einer stromdurchflossenen Spule die Stromstärke, so ändert sich der magnetische Fluß, weshalb nach dem Induktionsgesetz eine Spannung in die gleiche Spule induziert wird. Wegen der Energieerhaltung (Lenzsche Regel) ist die Spannung so gerichtet, dass sie die Zunahme oder Abnahme der Stromstärke hemmt.

Diese Selbst-Induktionsspannung ist proportional zur Änderung der Stromstärke. Die Induktivität der Spule ist der Proportionalitätsfaktor.

[math] U_i = L \dot I \quad \text{}[/math] Für eine "lange, dünne" Spule gilt: [math]L= \mu_0 \, \mu_r \, \frac{A\, n^2}{l}[/math]

Einführende Versuche

Versuch: Anschalten einer Lampe

Aufbau

Der Schaltplan mit Amperemeter.

Eine Spule (630Hy/280Ohm), eine Lampe (12V/0,1A) und ein Schalter sind in Reihe an eine Spannung von 30 Volt angeschlossen. Man schaltet ein und aus.

Beobachtung

Die Lampe leuchtet nicht sofort beim Umlegen des Schalters, sondern erst eine kurze Zeit später. (Video eines ähnlichen Versuchs.)

Offenbar gilt hier nicht das ohmsche Gesetz, nach dem Spannung und Stromstärke proportional sind!

Erklärung

Fließt durch die Spule ein Strom, so entsteht ein Magnetfeld, bzw. der Eisenkern wird magnetisiert. Nach dem Einschalten fließt der Strom nicht sofort, sondern steigt zunächst an. Durch die ansteigende Stromstärke steigt auch die Magnetisierung des Eisenkerns an, wodurch wiederum in der Spule eine Spannung induziert wird. Weil die Spule sowohl das Magnetfeld erzeugt, als auch in ihr die Induktionsspannung entsteht, spricht man von Selbstinduktion.

Diese Spannung ist offenbar so gerichtet, dass sie den Stromfluss hemmt. Man kann also sagen, dass nach dem Einschalten "die Spule geladen werden muss". Das Verhalten des Stromkreises kann man als Trägheit interpretieren. Der Stromfluss ist also durch den Aufbau des Magnetfeldes nicht ohne zeitliche Verzögerung zu ändern. Bei einem Wasserstromkreis entspricht dies der Trägheit des bewegten Wassers.

Versuch: Ausschalten eines Stromkreises

Aufbau

Ausschalten mit Glimmlampe

Der Schaltplan

• Zunächst wird eine Glimmlampe an eine Spannung von 30 Volt angeschlossen. Danach an eine Spannung von ca. 100 Volt.
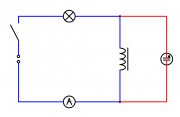
• Danach wird eine Spule (630Hy/280Ohm) über einen Schalter und ein Ampèremeter an die Spannungsquelle angeschlossen. Die Glimmlampe wird parallel zur Spule angeschlossen und der Schalter geschlossen und geöffnet.

Beobachtung

• Die Glimmlampe leuchtet erst bei einer höheren Spannung, und zwar an der dem Minuspol zugewandten Seite.
• Nur beim Unterbrechen des Stromkreises ist ein Aufleuchten der Glimmlampe zu sehen, und zwar auf der Seite, die mit dem Pluspol des Netzgerätes verbunden ist. (Video ohne Glimmlampe. Man beobachtet einen Öffnungsfunken am Schalter!)

Erklärung

Offenbar entsteht beim Ausschalten an der Glimmlampe eine hohe Spannung, welche anders gepolt ist als die Netzspannung.
Nach dem Öffnen des Schalters ist der mit dem Netzgerät verbundene blaue Stromkreis unterbrochen und somit kann auch das Netzgerät nicht die Glimmlampe betrieben haben. Die Energie für das Aufleuchten der Glimmlampe kann daher nur aus der Spule gekommen sein, die den neuen roten Stromkreis für eine kurze Zeit angetrieben hat.

Vor dem Ausschalten ist durch den Stromfluss in der Spule der Eisenkern magnetisiert. Nach dem Ausschalten nimmt diese Magnetisierung schnell ab. Durch die schnelle Abnahme des magnetischen Flusses wird in der Spule eine hohe Spannung induziert. Die Polung der Spannung an der Lampe kommt dadurch zustande, dass die Stromrichtung in der Spule sich durch das Ausschalten nicht ändert. Das Verhalten der Spule läßt sich als Trägheit interpretieren. Durch den Abbau der Magnetisierung unterstützt die Spule auch nach dem Ausschalten noch den Stromfluss. Bei einem Wasserstromkreis entspricht dies der Trägheit des bewegten Wassers.

Die Induktivität einer Spule

Wie hängt die Induktionsspannung einer Spule mit dem Stromfluss dieser Spule zusammen?

Die Induktionsspannung ist die Änderung des magnetischen Flusses. Da in diesem Fall die Fläche der Spule konstant ist, gilt:

[math]U_i = \dot \Phi = A \, \dot B[/math] Insbesondere gilt [math]U_i \sim \dot B[/math].

Die Flussdichte in der Spule ist proportional zur Stromstärke: [math]B \sim I[/math], deshalb folgt:

[math]U_i \sim \dot I \quad \Leftrightarrow \quad U_i = L \ \dot I[/math] Die Selbstinduktionspannung einer Spule ist proportional zur Änderung der Stromstärke. Die Proportionalitätskonstante heißt Induktivität der Spule. Sie ist ein Maß für die "elektrische Trägheit" der Spule.

Führt man die obige Überlegung vollständig aus und setzt die magnetische Feldstärke einer schlanken Spule ein, so erhält man:

[math] U_i = n\, \dot \Phi = n\,A\, \dot B = n\, A \, \mu_0 \, \mu_r\, \dot H = n\, A \, \mu_0 \, \mu_r \, \frac{n\,\dot I}{l} = \mu_0 \, \mu_r \, \frac{A\, n^2}{l} \quad \dot I[/math]

Also ist der gesuchte Proportionalitätsfaktor:

[math]L= \mu_0 \, \mu_r \, \frac{A\, n^2}{l} \qquad [L]=1\,\rm H \quad ("Henry")[/math] Die Induktivität einer schlanken Spule ist proportional zum Quadrat der Windungszahl, proportional zur Magnetisierbarkeit des Materials in der Spule sowie zur Spulenfläche und antiproportional zur Länge der Spule. Bei einer Spule mit der Induktivität von 2 Henry führt eine Änderung der Stromstärke von 1 A/s zu einer Induktionsspannung von 2 Volt.

Mit Hilfe der Induktivität kann man auch den magnetischen Fluss einer (schlanken) Spule berechnen. Die Induktionsspannung berechnet sich nämlich nach dem Induktionsgesetz zu:

[math] \begin{align} n\, \dot \Phi &= U_i = L \ \dot I \\ \Rightarrow \quad n\, \dot \Phi &= L\,\dot I \\ \Rightarrow \quad n\, \Phi &= L\,I \\ \end{align} [/math]

[math]\Phi = \frac{L\,I}{n}[/math] Der magnetische Fluss einer Spule ist proportional zu Induktivität und Stromstärke und antiproportional zur Windungszahl.

Anwendungen der Selbstinduktion

• Zündung beim Otto-Motor

Beschreiben sie, wie die Zündanlage bei einem Benzinmotor funktioniert. Vor allem der Aspekt Selbstinduktion und die Frage nach der Energie sind interessant.

Die Differentialgleichung des Ein- und Ausschaltvorgangs

NOCH ZU BEARBEITEN!!

Aufbau

Versuchsaufbau zur Computermessung

Schaltplan

Einschalten

Beobachtungen

Schaubilder von U(t) und I(t)

Erklärung

Potentialgebiete kurz dem Einschalten, nach einer "mittleren" Zeit und einer "langen" Zeit. Aufstellen der DGL nach der Maschenregel, bzw. den Potentialen Finden einer Lösung durch Probieren.

Diskussion des Ergebnisses: Man hat den ohmschen Widerstand der Spule vernachläßigt. Durch geeignete Wahl von L und R kann man die Kurve beim CASSY anpassen und so ein Wert für [math]\mu_r[/math] finden.

Anschaulich kann man sich dass so erklären:

• Direkt nach dem Einschalten ist die Änderung der Stromstärke groß, weshalb auch die Induktionsspannung groß ist. Die Induktionsspannung wirkt dem Stromfluss entgegen und somit fließt nur ein geringer Strom.
• Durch den Anstieg der Stromstärke erreicht diese bald einen größeren Wert, dass heisst, dass die entgegenwirkende Induktionsspannung kleiner geworden sein muss. Also ändert sich die Stromstärke nicht mehr so stark.

• [math]U_i = L \dot I[/math] Die Induktionsspannung ist proportional zur Änderung der Stromstärke. Die Induktivität der Spule ist der Proportionalitätsfaktor.

Links

• Video: An- und Ausschalten einer Lampe mit in Reihe geschalteter Spule. Man sieht die Verzögerung beim Anschalten und den Öffnungsfunken beim Ausschalten. (youtube: PHYSIKflothow Jörg Flothow, Leverkusen??)

• Video: Stromstärkeverlauf beim "Laden und Entladen" einer Spule (Theorie ab 1:50, Messung ab 6:50) "RLC Stromkreis" von Stephan Mueller auf youtube