Aufgaben zum Elektro-Magnetismus (Lösungen)
(Kursstufe > Elektro-Magnetismus)
Inhaltsverzeichnis
- 1 Magnetfelder um Ströme (Ampèrsches Gesetz)
- 2 Kraftwirkung auf elektrische Stöme im Magnetfeld
- 3 Grundlagen des Induktionsgesetzes
- 4 Anwendung des Induktionsgesetzes
- 5 Energieübertragung
- 6 Spule und Magnetfeld als Energiespeicher
- 7 Elektrische Wirbelfelder
- 8 Fußnoten
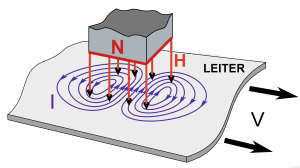
Magnetfelder um Ströme (Ampèrsches Gesetz)
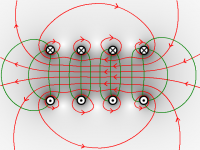
Magnetfeld von Kabel und Spule
Zeichnen Sie jeweils einige Feldlinien und Flächen ein und kennzeichnen Sie die Stromrichtung.
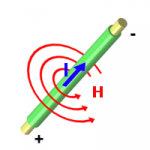
Die Rechte-Hand-Regel.
Magnetische Feldstärke
a) Wie wurde die schwere, elektrische und magnetische Feldstärke bereits mit Hilfe einer Probeladung definiert?
- Die Feldstärke wird als Ortsfaktor festgelegt:
- [math]\vec g=\frac{\vec F}{m} \qquad \vec E=\frac{\vec F}{q} \qquad \vec H=\frac{\vec F}{q_m} [/math]
b) Warum ist diese Festlegung im elektrischen und schweren Fall praktikabel, aber im magnetischen Fall nicht?
- Die Messvorschriften für die Masse und den elektrischen Strom sind so festgelegt, dass man damit relativ einfach mit einer Waage die Masse und die elektrische Ladung mit Hilfe einer Stromstärkemessung bestimmen kann. Das gilt nicht für die magnetische Ladung. Ohne die Messung der magnetischen Ladung kann man aber die Feldstärke nicht als Kraft pro Ladung bestimmen.
c) Wie wird daher die magnetische Feldstärke definiert?
- Die magnetische Feldstärke wird mit Hilfe einer schlanken Spule festgelegt.
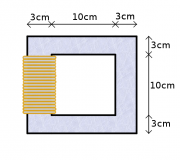
Feldstärken berechnen
a) Eine Spule ist 60cm lang, hat einen Durchmesser von 15cm und 2000 Windungen. Es fließt ein Strom der Stärke 300mA durch das Kabel. Berechnen Sie die magnetische Feldstärke innerhalb der Spule.
- Die Spule ist wesentlich länger als ihr Durchmesser, daher ist es gerechtfertigt von einer "schlanken" Spule zu sprechen, bei sich nur innerhalb ein homogenes Magnetfeld befindet. Der Durchmesser der Spule muss daher nicht berücksichtigt werden:
- [math]H = \frac{n\, I}{l} = \frac{2000\cdot 0{,}3\,\rm A}{0{,}6\,\rm m} = 1000\,\rm \frac{A}{m}[/math]
b) Ist es egal, ob die Spule einen Durchmesser von 15cm oder von 30cm hat?
- Je kleiner der Durchmesser im Verhältnis zur Länge der Spule ist, desto genauer ist die Näherung einer "schlanken Spule". Bei einem Durchmesser von 30cm ist die Feldstärke im Inneren der Spule schon wesentlich geringer als man mit der Formel für die schlanke Spule berechnet. Man kann die Feldstärke für den Mittelpunkt der Spule auch in Abhängigkeit von ihrem Durchmesser und ihrer Länge berechnen. Eine ganz kurze Spule, also eine Leiterschleife, und eine ganz dünne, schlanke Spule ergeben sich als Grenzfälle:
Leiterschleife [math]l=0[/math]
beliebige Länge [math]l[/math]
beliebiger Radius [math]r[/math]schlanke Spule [math]r=0[/math]
[math]H=\frac{n\,I}{2\,r}[/math]
[math]H=\frac{n\,I}{\sqrt{4\,r^2 + l^2}}[/math]
[math]H=\frac{n\,I}{l}[/math]
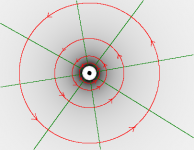
c) Durch ein Kabel fließt ein Strom mit der Stärke von 20 Ampère. Berechnen Sie die magnetische Feldstärke in einem Abstand von 1cm, 2cm und 3cm vom Kabel.
- Um die Feldstärke zu bestimmen läuft man einen geschlossenen Weg entlang einer Feldlinie um das Kabel herum. Der Weg hat die Länge eines Kreises: [math]l=2\pi\,r[/math] Die Feldstärke entlang einer Feldlinie ist hier konstant. Nach dem Ampèreschen Gesetz gilt:
- [math]H\, l = I \quad \Rightarrow \quad H=\frac{I}{2\pi\,r}[/math]
- Damit ergibt sich bei einem Abstand von 1cm:
- [math] H(1\,\rm cm)=\frac{20\,\rm A}{2\pi\cdot 0{,}01\,\rm m} =\frac{20\,\rm A}{0{,}0628\,\rm m} = 318\,\rm\frac{A}{m}[/math]
- Im doppelten, bzw. dreifachen Abstand verdoppelt und verdreifacht sich auch die Weglänge und somit geht die Feldstärke auf die Hälfte oder auf ein Drittel zurück:
- [math] H(2\,\rm cm)= 159\,\rm\frac{A}{m}\qquad H(3\,\rm cm)= 106\,\rm\frac{A}{m}[/math]
Horizontalkomponente des Erdmagnetfeldes
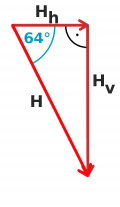
Die Feldlinien des Erdmagnetfeldes verlaufen nur am Äquator parallel zur Erdoberfläche und in geographischer Süd-Nord-Richtung. In Deutschland bilden die Feldlinien mit dem Erdboden einen sogenannten Inklinationswinkel von ungefähr 64°. Die horizontale Komponente ist also in Deutschland kleiner als die senkrecht in den Boden weisende, vertikale Komponente.
Mit Hilfe einer Spule und eines Kompasses kann man relativ einfach die horizontale Komponente des Erdmagnetfeldes messen. Dazu legt man die Spule in West-Ost-Richtung auf einen Tisch und stellt einen Kompass in die Spule, der sich dann nach Norden ausrichtet. Jetzt läßt man genau soviel Strom durch die Spule fließen, bis die Kompassnadel entweder nach Nord-Ost oder nach Nord-West zeigt. (Wovon hängt das ab?)
a) Die Spule ist 30cm lang und hat 100 Windungen. Bei einer Stromstärke von 48mA zeigt die Nadel genau nach Nord-Ost. Berechnen Sie daraus die Horizontalkomponente.
- Innerhalb der Spule überlagert sich das Erdmagnetfeld mit dem Feld der Spule. Der Kompass zeigt die Richtung der Summe von Horizontalkomponente und Spulenfeld an. Der Kompass hat sich um 45° gedreht, weshalb die Feldstärke des Spulenfeldes genauso groß sein muss wie die Horizontalkomponente:
- [math]H_h = H_s = \frac{n\, I}{l}= \frac{100\cdot 0{,}048\,\rm A}{0{,}3\,\rm m} = 16\,\rm \frac{A}{m} [/math] [1]
b) Berechnen Sie mit Hilfe des Inklinationswinkels von 64° auch die vertikale Komponente und die gesamte Feldstärke des Erdmagnetfeldes.
- In dem rechtwinkligen Dreieck kennt man eine Kathete und einen Winkel. Man sucht die Hypothenuse und die andere Kathete. Das geht am einfachsten mit den Winkelfunktionen:
- [math]\tan(64^\circ) = \frac{H_v}{H_h} \quad \Rightarrow \quad H_v = \tan(64^\circ) \cdot H_h = \tan(64^\circ) \cdot 16\,\rm \frac{A}{m} = 2{,}05 \cdot 16\,\rm \frac{A}{m} = 32{,}8\,\rm \frac{A}{m} [/math]
- Die Hypothenuse kann man jetzt, nachdem man beide Katheten kennt, auch mit dem Satz des Pythagoras berechnen. Hier aber nochmal der Rechenweg mit einer Winkelfunktion:
- [math]\cos(64^\circ) = \frac{H}{H_h} \quad \Rightarrow \quad H = \cos(64^\circ) \cdot H_h = \cos(64^\circ) \cdot 16\,\rm \frac{A}{m} = 0{,}438 \cdot 16\,\rm \frac{A}{m} = 7{,}0\,\rm \frac{A}{m} [/math]
Messen der magnetischen Ladung
a) Beschreiben Sie ein Verfahren, mit dem man die magnetische Ladung eines Festmagneten bestimmen kann.
- Die Formel für den Ortsfaktor wird als Festlegung der magnetischen Ladung interpretiert:
- [math]H=\frac{F}{q_m} \quad \Rightarrow \quad q_m = \frac{F}{H}[/math]
- Die zu messende magnetische Ladung befindet sich in einem Magnetfeld einer Spule. Die magnetische Feldstärke ist daher berechenbar und die Kraftwirkung kann man einfach messen. Das wird in diesem Praktikum beschrieben.
b) Der Nordpol eines Dauermagneten erfährt im Inneren einer Spule eine Kraft von 0,3N. Die Spule hat 500 Windungen und es fließt ein Strom der Stärke 2A hindurch. Die Länge der Spule beträgt 10cm. b1) Wieviel magnetische Ladung "sitzt" auf dem Nordpol?
- Wenn man keine große Genauigkeit erwartet, kann man die Spule, obwohl sie im Verhältnis zur Länge relativ breit ist, als "schlanke" Spule ansehen und damit die Feldstärke berechnen:
- [math]H = \frac{n\,I}{l} = \frac{500\,2\,\rm A}{0{,}10\,\rm m} = \frac{1000\,\rm A}{0{,}10\,\rm m} = 10000\,\frac{\rm A}{\rm m} = 10000\,\frac{\rm N}{\rm Wb} [/math]
- [math]q_m = \frac{F}{H} = \frac{0{,}3\,\rm N}{10000 \rm \frac{N}{Wb}} = 3\cdot 10^{-5}\,\rm Wb = 30\,\rm \mu Wb [/math]
- Der Zahlenwert für die magnetische Ladung ist sehr klein. Das Weber ist offensichtlich, ähnlich wie das Coulomb, eine sehr große Einheit.
b2) Wieso ist es wichtig, dass der Südpol relativ weit entfernt ist?
- Bei der Kraftmessung wird immer die Kraft auf den gesamten Magneten, also auch die Wirkung auf den Südpol, bestimmt. Ist der Südpol aber an einer Stelle, an der das Magneteld schwach ist, so ist die Verfälschung der Messung gering.
b3) Was erwarten Sie, wenn man die Kraftwirkung auf den Südpol misst? (Was folgt daraus?)
- Die Nord- und Südpolladung eines Magneten ist immer gleich groß. Die Summe der Ladungen ist Null. Das kann man mit Hilfe dieses Experimentes auch nachweisen!
- Das Messergebnis unterstützt die Theorie der "Elementarmagnete". Der Festmagnet hat an den Enden Pole, weil er magnetisch polarisiert (magnetisiert) ist. Das heißt, die Elementarmagnete des Magneten sind ausgerichtet. Elementarmagnete sind Dipole und tragen genausoviel Nordpol- wie Südpolladung.
Kraftwirkung auf elektrische Stöme im Magnetfeld
Zug- und Druckspannungen im Magnetfeld
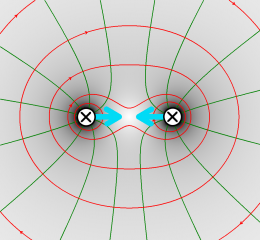
Kraft zwischen (anti-)parallelen Strömen I
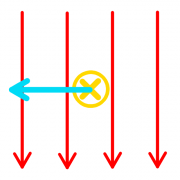
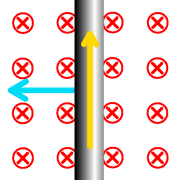
In den Zeichnungen ist ein senkrechter Schnitt durch zwei stromdurchflossene parallele Kabel dargestellt. Die Stromrichtung ist durch ein Kreuz oder einen Punkt markiert. a) Zeichnen Sie einige Feldlinien in roter Farbe und einige Feldflächen in grüner Farbe ein.
b) Wie wirkt das Magnetfeld auf die Kabel? Zeichnen Sie Kraftpfeile ein.
c) Erklären Sie die Kraftwirkung mit Hilfe von Zug- und Druckspannungen.
- Längs der Feldlinien steht das Magnetfeld unter Zugspannung, längs der Flächen unter Druckspannung. "Die Feldlinien sind wie sich abstoßende Gummibänder." (Vgl. hier)
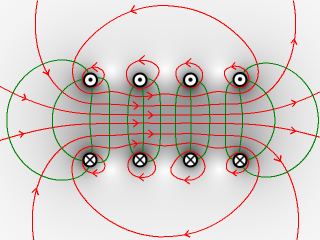
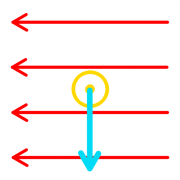
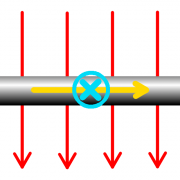
Kräfte auf Kabel und Spule
Hier ist der senkrechte Schnitt durch ein stromdurchflossenes Kabel und eine stromdurchflossene Spule dargestellt.
- a) Zeichnen Sie einige Feldlinien (rot) und Feldflächen (grün) ein.
- b) Welche Wirkung haben die Zug- und Druckspannungen auf das Kabel und welche auf die Spule?
Strom verändert das homogene Feld
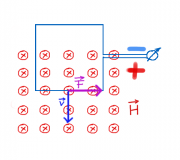
Ein stromdurchflossenes Kabel befindet sich zwischen den Polen eines Rechteckmagneten. Durch das Magnetfeld des Kabels verändert sich das Feld zwischen den Polen. a) Zeichen Sie einige Feldlinien (rot) und Flächen (grün) ein.
b) Erklären Sie die Kraftwirkung mit Hilfe von Zug- und Druckspannungen.
c) Erläutern Sie die "Drei-Finger-Regel" oder auch "UVW-Regel" und kennzeichnen Sie die Richtung der Lorentzkraft mit einem Pfeil. Warum verwenden manche die linke und manche die rechte Hand?
- Die Antworten werden im "Leiterschaukel-Versuch" erläutert.
Lorentzkraft auf Probeströme im Feld
Richtung der Lorentzkraft
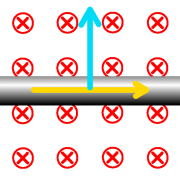
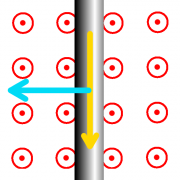
Ein stromdurchflossenes Kabel befindet sich in einem homogenen Magnetfeld. Die (technische) Stromrichtung ist mit einem gelben Pfeil gekennzeichnet, die Feldlinienrichtung mit einem roten und die Richtung der Kraft mit einem blauen Pfeil.
- Ergänzen Sie in den Zeichnungen die fehlende Kraft-, Strom oder Feldlinienrichtung in der entsprechenden Farbe.
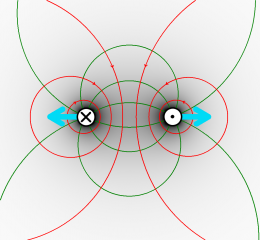
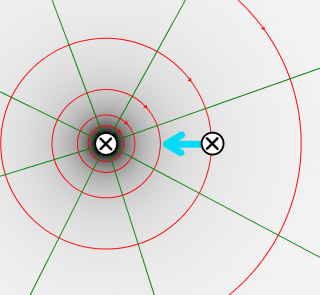
Kraft zwischen (anti-)parallelen Strömen II
Dargestellt ist der senkrechte Schnitt durch zwei parallele Kabel und die Stromrichtungen.
Die Kabel sind 3cm voneinander entfernt und einen halben Meter lang. (Die Dicke der Kabel wird vernachlässigt.) Durch das linke Kabel fließt ein Strom der Stärke von 20 Ampère, durch das rechte ein Strom der Stärke von 3 Ampère.
Um die Kraftwirkung auf das rechte Kabel zu berechnen, betrachtet man den rechten Strom als Probestrom im Feld des linken Kabels.
a) Zeichen Sie einige Feldlinien des Magnetfeldes des linken Kabels ein.
b) Bestimmen Sie mit der Drei-Finger-Regel die Richtung der Lorentzkraft auf den rechten Strom und zeichnen Sie die Kraftrichtung ein.
c) Berechnen Sie die Feldstärke des linken Magnetfeldes an der Stelle, an der sich das rechte Kabel befindet.
- Nach dem Ampèrschen Gesetz gilt:
- [math]H=\frac{I}{l} =\frac{I}{2\pi\,r} =\frac{20\,\rm A}{2\pi\cdot 0{,}03\,\rm m} =\frac{20\,\rm A}{0{,}188\,\rm m} =106\rm\frac{A}{m}[/math]
d) Berechnen Sie nun die Lorentzkraft auf den rechten Leiter.
- Dazu braucht man die Formel für die Lorentzkraft auf einen Leiter:
- [math]F=\mu_0 \, H \, I \, l [/math]
- Achtung! Der Buchstabe [math]l[/math] steht hier für die Länge des Leiters, im Ampèrschen Gesetz steht [math]l[/math] für die Länge eines geschlossenen Weges!
- [math]F= 1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 106\rm\frac{A}{m} \cdot 3\,\rm A \cdot 0{,}5\,\rm m = 2{,}0 \cdot 10^{-4}\,\rm N = 0{,}20 \,\rm mN [/math]
- Die Kraft ist also ziemlich klein.
- Man kann statt dem Zahlenwert der Feldstärke auch das Ampèrsche Gesetz einsetzen und erhält eine allgemeine Formel für die Kraft zwischen zwei parallelen Leitern. Zur Unterscheidung der beiden Stromstärken wird die Probestromstärke in Kleinbuchstaben geschrieben:
- [math]F=\mu_0 \, H \, i \, l =\mu_0 \, \frac{I}{2\pi\,r} \, i \, l = 2\pi\, \mu_0 \, \frac{I\, i}{r}\, l[/math]
- Man kann das mit den Abstandsgesetzen von Massen und Ladungen vergleichen. (Gravitationsgesetz und Coulombsche Gesetze)
e) Berechnen Sie nach der gleichen Methode die Lorentzkraft auf den linken Leiter. Überrascht Sie das Ergebnis?
- Man berechnet also die Feldstärke des rechten Kabels an der Stelle des linken Kabels:
- [math]H =\frac{I}{2\pi\,r} =\frac{3\,\rm A}{0{,}188\,\rm m} =15{,}9\rm\frac{A}{m}[/math]
- [math]F= 1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 15{,}9\rm\frac{A}{m} \cdot 20\,\rm A \cdot 0{,}5\,\rm m = 2{,}0 \cdot 10^{-4}\,\rm N = 0{,}20 \,\rm mN [/math]
- Es kommt also die gleiche Kraft raus! Alles andere wäre auch unlogisch, denn nach der Impulserhaltung oder dem Prinzip "actio gleich reactio" muss das Magnetfeld an beiden Kabeln mit der gleichen Kraft ziehen.
Auch die Formel [math]F= 2\pi\, \mu_0 \, \frac{I\, i}{r}\, l[/math] hat diese Symmetrie. Es ist egal, ob man I mit i vertauscht oder nicht.
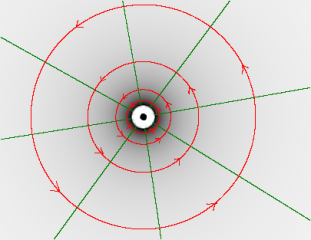
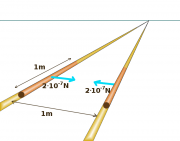
Definition des Ampères
Die Einheit der elektrischen Stromstärke, das Ampère, ist eine der sieben Basiseinheiten des internationalen Einheitensystems (SI). Alle weiteren Einheiten lassen sich auf diese sieben Basiseinheiten zurückführen. Mit Hilfe von sieben mehr oder weniger praktikablen Messvorschriften wird jeweils eine Einheit festgelegt. Die Definition des Ampères lautet (noch bis ca. 2018):
Das Ampere ist die Stärke eines konstanten elektrischen Stromes, der, durch zwei parallele, geradlinige, unendlich lange und im Vakuum im Abstand von einem Meter voneinander angeordnete Leiter von vernachlässigbar kleinem, kreisförmigem Querschnitt fließend, zwischen diesen Leitern je einem Meter Leiterlänge die Kraft [math]2 \!\cdot\! 10^{–7}[/math] Newton hervorrufen würde.
Die Festlegung des Ampères gehört offensichtlich zu den nicht praktikablen Festlegungen. Aber wieso diese scheinbar willkürliche Kraft von [math]2 \!\cdot\! 10^{–7}[/math] Newton pro Meter?
Berechnen Sie dazu die Kraft, die auf ein ein Meter langes Teilstück dieser "unendlich" langen Leiter ausgeübt wird. (Vergleiche dazu die Aufgabe "Kraft zwischen (anti-)parallelen Strömen II"!)
- Man kann ein Kabel als Probestrom im Magnetfeld des anderen betrachten. Die Feldstärke eines Kabels in einem Abstand von 1m beträgt nach dem Ampèreschen Gesetz:
- [math]H=\frac{I}{l} =\frac{I}{2\pi\,r} =\frac{1\,\rm A}{2\pi\cdot 1\,\rm m}=\frac{1}{2\pi} \,\rm \frac{A}{m}[/math]
- Die Lorentzkraft auf ein ein Meter langes Teilstück beträgt damit:
- [math]F=\mu_0 \, H \, I \, l = 1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot \frac{1}{2\pi} \,\rm\frac{A}{m} \cdot 1\,\rm A \cdot 1\,\rm m = 2{,}00 \cdot 10^{-7}\,\rm N[/math]
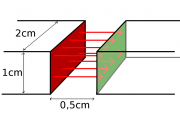
Feldstärkemessung mit Probestrom
Um die magnetische Feldstärke eines Elektromagneten zu messen, hängt man ein 2cm langes Leiterstück senkrecht zu den Feldlinien in das Magnetfeld und misst die darauf wirkende Lorentzkraft. Bei einer Stromstärke von 20A bestimmt man die Kraftwirkung zu 35mN.
Berechnen Sie die Feldstärke des Magnetfeldes.
- Die Formel für die Lorentzkraft kann man nach der Feldstärke auflösen:
- [math]\begin{alignat}{2} & F &=& \mu_0 \, H \, I \, l & \\ \Rightarrow & H &=& \frac{F}{\mu_0\,I\,l} \\ & &=& \frac{35\cdot 10^{-3}\,\rm N}{1{,}26 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 20\,\rm A \cdot 0{,}02\,\rm m} \\ & &=& 69400\,\rm\frac{A}{m} \end{alignat} [/math]
Kabel im Erdmagnetfeld
Das Erdmagnetfeld hat in Deutschland eine Stärke von ca. 40A/m. (Das entspricht ca. 50 mikroTesla.)
a) Welche Kraft erfährt ein Stromkabel, dass von 20A durchflossen wird und 1m lang ist maximal?
- Die maximale Lorentzkraft beträgt:
- [math] F = \mu_0 \, H \, I \, l =1{,}26 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}}\cdot 40\,\rm\frac{A}{m}\cdot 20\,\rm A \cdot 1\,\rm m = 1 \,\rm mN[/math]
b) Wie muss man das Kabel ausrichten, um die wirkende Kraft möglichst groß oder möglichst klein zu haben?
- Wenn das Kabel senkrecht zu den Feldlinien verläuft, also in West-Ost-Richtung, dann ist die Kraft maximal. Richtet man das Kabel parallel zu den Feldlinien aus, also in Nord-Süd-Richtung und in Deutschland ca. 64° zum Erdboden geneigt, dann gibt es gar keine Kraft auf das Kabel.
Lorentzkraft auf bewegte Ladungen im Magnetfeld
Flugbahnen
Die geladenen Teilchen bewegen sich auf ein begrenztes und homogenes Magnetfeld zu.
- a) in welche Richtung wirkt beim Eintauchen in das Magnetfeld die Lorentzkraft?
- b) Beschreiben Sie die Bahnkurve der Teilchen nach dem Eintauchen und skizzieren Sie eine mögliche in der Zeichnung.
Sonnenwind trifft auf das Erdmagnetfeld
Der sogenannte "Sonnenwind" besteht aus schnellen, elektrisch positiv oder negativ geladenen Teilchen, die von der Sonne ausgesendet werden. In der Zeichnung sind vier Teilchen und deren Bewegungsrichtung eingezeichnet.
- Kennzeichnen Sie die Kraftrichtung auf die Teilchen mit einem Pfeil.
- Erklären Sie wie sich die Bahn der Teilchen durch das Erdmagnetfeld ändert.
Blasenkammer
Massenspektrometer
Wienscher Geschwindigkeitsfilter
Hall-Sonde
- Erklären Sie die prinzipielle Funktionsweise einer Hall-Sonde.
- Eine Hall-Sonde besteht aus einem Leiterstück, durch das Strom fließt und sich in einem Magnetfeld befindet. Die bewegten Ladungen (bei Metallen Elektronen) werden durch das Magnetfeld bzw. durch die wirkende Lorentzkraft von ihrer Bahn abgelenkt. In der Sonde entsteht nun eine Ladungstrennung (Spannung) senkrecht zur Bewegungsrichtung der Ladungen und senkrecht zu den magnetischen Feldlinien.
- Die Spannung kann man messen und mit ihrer Hilfe die Stärke des Magnetfeldes berechnen.
Die Zeichnung kann
- mit "Strg" + linke Maustaste gedreht werden,
- mit "Shift" + linke Maustaste verschoben werden
- (klicken mit der linken Maustaste ändert die Verschiebungsrichtung) und
- mit dem Mausrad vergrößert oder verkleinert werden.
- Es wird der Hall-Effekt bei einem Halbleiter und bei Silber untersucht. Folgende Messwerte wurden gefunden:
- Silber: (effektive) Länge l=5mm Höhe h=2cm Dicke d=0,1mm Stromstärke I=20A, Hallspannung U= 0,01 mV
- Germanium, p-dotiert: Länge l=10mm Höhe h=5mm Dicke d=1mm Stromstärke I=80mA, Hallspannung U= -40mV
- In beiden Fällen betrug die magnetische Feldstärke 80000A/m.
- a) Berechnen Sie jeweils die Geschwindigkeiten der Ladungsträger.
- Auf die Ladungsträger wirkt die Lorentzkraft und eine gleich große, entgegengesetzte elektrische Kraft. (Hier steht die ausführliche Erklärung.) Daraus läßt sich die Hallspannung berechnen:
- [math]U_H = \mu_0\, v \, H \, h[/math]
- Nun kann man nach der Geschwindigkeit auflösen:
- Silber: [math]v_S =\frac{U_H}{\mu_0 \, H \, h} = \frac{0{,}01 \cdot 10^{-3}\,\rm V}{1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 80000\,\rm \frac{A}{m} \cdot 0{,}02\,\rm m} = 4{,}98\cdot 10^{-3}\,\rm\frac{m}{s} \approx 5{,}0\,\rm \frac{mm}{s}[/math]
- Germanium: [math]v_G = \frac{40 \cdot 10^{-3}\,\rm V}{1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 80000\,\rm \frac{A}{m} \cdot0{,}005\,\rm m} = 79{,}6\,\rm\frac{m}{s}[/math]
- Die Elektronen im Silber "schleichen" also nur dahin, während die Löcher des dotierten Germaniums mit fast 300 km/h sausen! Das liegt daran, dass es im Silber viele Elektronen pro Volumen gibt, welche die Ladung transportieren und im Germanium aber nur wenige Löcher. Um die gleiche Stromstärke zu erreichen, müssen die Löcher viel schneller sein als die Elektronen.
- b) Warum ist das Vorzeichen der Hallspannung unterschiedlich?
- Das kann man gut an der obigen Animation sehen: Bei einer Stromrichtung von links nach rechts bewegen sich die positiven Löcher im Germanium nach rechts, die Elektronen im Silber aber nach links. Mit Hilfe der Drei-Finger-Regel findet man, dass die Lorentzkraft in beiden Fällen nach oben wirkt. Die entstehende Ladungstrennung, und damit die Spannung, ist dadurch unterschiedlich.
Grundlagen des Induktionsgesetzes
Verschiedene Wege zur Induktionsspannung
Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese.
- Eine Leiterschleife in ein Magnetfeld eintauchen (herausziehen).
- Durch das Eintauchen vergrößert (verringert) sich die "Anzahl der Feldlinien" durch die Schleife, genauer nimmt der magnetische Fluss durch die Schleife zu (ab). Es wird eine Spannung an der Schleife erzeugt (andere Polung).
- Eine Leiterschleife in einem Magnetfeld vergrößern (verkleinern). Auch hier darf die Schleife dabei nicht parallel zu den Feldlinien sein.
- Wiederum nimmt der magnetische Fluss durch die Schleife zu (ab).
- Der Nordpol eines Festmagneten wird der Schleife genähert.
- Die Feldstärke ist in der Nähe des Pols größer, deshalb nimmt der magnetische Fluss durch die Schleife zu.
- Die Schleife befindet sich im Magnetfeld einer Spule. Der Strom durch die Spule steigt an (nimmt ab).
- Durch die Zunahme des Stromes steigt auch die Feldstärke innerhalb der Spule an und somit der magnetische Fluss durch die Schleife. (Bei abnehmender Stromstärke sinkt der Fluss und die Polung der Spannung ist umgekehrt.)
- Die Schleife befindet sich um einen Eisenkern. Der Pol eines Festmagneten wird dem Eisenkern genähert.
- Durch die Annäherung des Magneten vergrößert sich die Magnetisierung des Eisens und der magnetische Fluss durch die Schleife nimmt zu.
- Die Schleife und eine Spule befinden sich um einen Eisenkern, sie sind "induktiv gekoppelt". Durch die Spule fließt ein Strom mit zunehmender Stromstärke.
- Der Spulenstrom führt zu einer Magnetisierung des Eisenkerns. Da die Stromstärke zunimmt, steigt auch die Magnetisierung mit der Zeit an. Dadurch steigt der magnetische Fluss durch die Schleife an und eine Spannung wird erzeugt.
- Eine Schleife wird in einem Magnetfeld gedreht. Die Drehachse ist nicht parallel zu den Feldlinien.
- Je nach Lage der Schleife "gehen viele oder wenige Feldlinien durch die Schleife", der magnetische Fluss ist groß oder klein. Ist die Schleife parallel zu den Feldlinien, so verschwindet der Fluss durch die Schleife. Die Drehung führt daher zu einer Änderung des magnetischen Flusses durch die Schleife und somit zu einer Induktionsspannung.
Magnetischer Fluss
Erläutern Sie anhand von verschiedenen Beispielen, was der magnetische Fluss durch eine Fläche ist.
- Hält man den Pol eines Festmagneten nahe vor eine Leiterschleife, so ist der magnetische Fluss durch die von der Schleife umrandete Fläche groß, weil "viele Magnetfeldlinien" durch die Fläche gehen. Genauer ist das Produkt von mittlerer Feldstärke und Fläche groß.
- Hält man den Festmagneten so an die Schleife, dass die Feldlinien parallel zur Schleife sind, so verlaufen gar keine Feldlinien durch die Fläche und der magnetische Fluss verschwindet. In diesem Fall ist das Produkt von Feldstärke und Fläche Null, weil die effektive Fläche senkrecht zu den Feldlinien Null ist.
- Befindet sich ein magnetisierter Eisenkern in einer Leiterschleife, so gibt es einen magnetischen Fluss durch die Fläche der Schleife, weil "viele Magnetisierungslinien" durch die Fläche gehen. Genauer ist der magnetische Fluss das Produkt aus mittlerer Magnetisierung und Fläche.
Induktionsgesetz
- Wie lautet das Induktionsgesetz in Worten?
- Die Induktionsspannung an einer Leiterschleife ist die zeitliche Änderung des magnetischen Flusses.
- Wie lautet das Induktionsgesetz als Formel in den folgenden Situationen:
- Die Formeln gelten für eine Induktionsspule mit n Windungen.
- Der magnetische Fluss ist:
- [math]\Phi = \mu_0 \, H \, A + \mu_0 \, M \, A = \mu_0 \mu_r \, H \, A [/math]
- Allgemeingültig
- [math]U_i = n \, \dot \Phi[/math]
- Ohne Magnetisierung, nur die Feldstärke ändert sich, die Schleifenfläche ist konstant.
- [math]U_i = n \, \mu_0 \, \dot H \, A \approx n \, \mu_0 \, \frac{\Delta H}{\Delta t}\, A[/math]
- Ohne Magnetisierung, nur die Schleifenfläche ändert sich, die Feldstärke ist konstant.
- [math]U_i = n \, \mu_0 \, H \, \dot A \approx n \,\mu_0 \, H \, \frac{\Delta A}{\Delta t}[/math]
- Ohne Feld, nur die Magnetisierung ändert sich, die Schleifenfläche ist konstant.
- [math]U_i = n \, \mu_0 \, \dot M \, A \approx n \, \mu_0 \, \frac{\Delta M}{\Delta t} \, A[/math]
Anwendung des Induktionsgesetzes
Primär und Sekundärspule
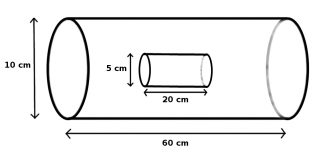
Innerhalb einer "großen" Primärspule mit 500 Windungen liegt eine "kleine" Sekundärspule mit 2000 Windungen. (Siehe Zeichnung) Durch die Primärspule fließt ein Strom von zwei Ampère.
Die Spule wird dann von der Spannungsquelle getrennt, wodurch die Stromstärke innerhalb von einer tausendstel Sekunde auf Null Ampère zurückgeht.
a) Wie groß ist zu Beginn die magnetische Feldstärke? Berechnen Sie den magnetischen Fluss durch die Primär- und die Sekundärspule.
- Die Spule betrachtet man als "schlanke Spule" und berechnet dann nach der Definition der magnetischen Feldstärke:
- [math]H=\frac{n_1\, I}{l}= \rm \frac{500\cdot 2\,A}{0{,}6\,m}= \rm 1667\, \frac{A}{m}[/math]
- Die Luft ist nicht magnetisierbar, deswegen ist die Flussdichte einfach das Produkt der Feldstärke mit der Feldkonstante:
- [math]B=\mu_0\,H = 1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \cdot 1667\, \rm \frac{A}{m}= 0{,}002095\,\rm\frac{Vs}{m^2}[/math]
- [math]\rm \text{} \quad (= 2{,}095\cdot 10^{-3}\,\frac{Wb}{m^2}= 2{,}095 \,mT)[/math]
- Die Fläche der Spulen berechnen sich mit Hilfe des Radius:
- [math]A_1=\pi\, r_1^2 = \pi\cdot (0{,}05\,\rm m)^2 = 0{,}007854\,\rm m^2 \quad (= 78{,}54\,\rm cm^2)[/math]
- [math]A_2=\pi\, r_2^2 = \pi\cdot (0{,}025\,\rm m)^2 = 0{,}001969\,\rm m^2 \quad (= 19{,}69\,\rm cm^2)[/math]
- Aus der Flussdichte und der Fläche kann man nun den magnetischen Fluss berechnen:
- [math]\Phi_1 = B\, A_1 = 2{,}095\cdot 10^{-3}\,\rm\frac{Wb}{m^2} \cdot 0{,}007854\,\rm m^2 = 1{,}645\cdot 10^{-5}\,\rm Wb \quad (V s\,\text{oder}\,T m^2)[/math]
- [math]\Phi_2 = B\, A_2 = 2{,}095\cdot 10^{-3}\,\rm\frac{Wb}{m^2} \cdot 0{,}001969\,\rm m^2 = 4{,}114\cdot 10^{-6}\,\rm Wb [/math]
b) Während des Trennens von der Spannungsquelle registriert die Sekundärspule eine Spannung. Begründen Sie dies und berechnen Sie die Spannung.
- Durch die fehlende Spannung sinkt die Stromstärke auf Null ab. Währenddessen ändert sich die Feldstärke und damit auch der magnetische Fluss in der Sekundärspule.
- Zur Berechnung der Induktionsspannung verwendet man das Induktionsgesetz:
- [math]U_i = n_2\,\dot \Phi = n_2\,\frac{\Delta \Phi}{\Delta t} =2000\cdot \frac{4{,}114\cdot 10^{-6}\,\rm Wb}{10^{-3}\,\rm s} = 8{,}23\,\rm V \qquad \left(\rm\frac{Wb}{s} = \rm\frac{V s}{s} \right)[/math]
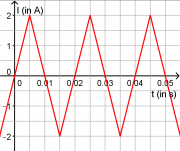
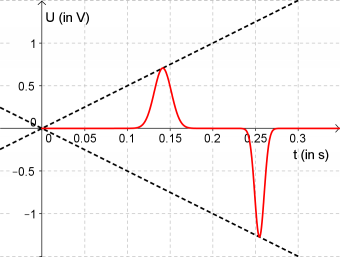
Danach legt man an die Primärspule eine Dreiecksspannung mit einer Frequenz von 50Hz an, die zu einer maximalen Stromstärke von 2A führt. (Siehe Zeichnung) Zur Messung der Spannung an der Sekundärspule wird ein Oszilloskop angeschlossen.
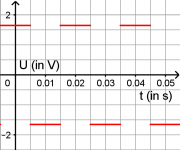
c) Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der mit dem Oszilloskop gemessenen Induktionsspannung ein.
- Wieder wird durch die Änderung der Stromstärke der magnetische Fluss geändert.Im Induktionsgesetz kann man sich nun aussuchen, welche Änderungsrate man ausrechnet. Man kann die Änderung der Flussdichte, der Feldstärke oder der Stromstärke verwenden:
- [math]U_i = n_2\,\dot \Phi = n_2 \,\dot B\, A = n_2 \,\mu_0 \dot H \, A = n_2 \,\mu_0 \frac{n_1}{l} \dot I \, A \qquad \left(= \mu_0 \, \frac{A\, n_1\, n_2}{l} \cdot \dot I \right)[/math][2]
- Weil hier die Stromstärke sich konstant ändert, kann man die Änderungsraten als Differenzenquotient berechnen:
- [math]U_i = n_2 \,\frac{\Delta \Phi}{\Delta t} = n_2 \,\frac{\Delta B}{\Delta t}\, A = n_2 \,\mu_0\frac{\Delta H}{\Delta t}\, A = n_2 \,\mu_0 \frac{n_1}{l}\frac{\Delta I}{\Delta t}\, A[/math]
- Die Stromstärke fällt oder oder steigt innerhalb von [math]0{,}01\,\rm s[/math] um [math]4\,\rm A[/math]:
- [math]\frac{\Delta I}{\Delta t} = \rm \frac{4\,A}{0{,}01\,\rm s} = 400\,\rm\frac{A}{s}[/math]
- Bei ansteigender Stromstärke beträgt die Induktionsspannung daher:
- [math]U_i = n_2\,\mu_0 \frac{n_1}{l}\frac{\Delta I}{\Delta t}\, A = 2000\cdot 1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \cdot \frac{500}{0{,}6\,\rm m}\cdot \frac{4\,\rm A}{0{,}01\,\rm s}\, 0{,}001969\,\rm m^2 = 0{,}165\,\rm V \quad (= 165\,\rm mV)[/math]
- Jetzt kann man den Verlauf der Induktionsspannung zeichnen.
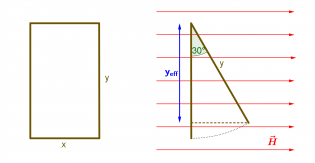
Wie ändert sich der Verlauf der Induktionsspannung, wenn die Sekundärspule in einem Winkel von 30° in der Primärspule liegt?
- Nun ist die von der Flussdichte durchsetzte effektive Schleifenfläche kleiner, also sinkt auch die Induktionsspannung, die proportional zur Fläche ist.
- Die Abnahme läßt sich auch berechnen. Der Einfachheit halber nimmt man zunächst eine Schleife mit rechteckiger Fläche. Durch die 30°-Drehung verkürzt sich die effektive Länge [math]y_{eff}[/math] der Rechteckschleife:
- [math]\cos(30^\circ)=\frac{y_{eff}}{y}\quad \Rightarrow \quad y_{eff}= \cos(30^\circ) \, y = \frac{\sqrt 3}{2} \, y \approx \, 0{,}87 \cdot y[/math]
- Die Breite x des Rechtecks bleibt unverändert, daher verkleinert sich die Fläche auf 87%:
- [math] A_{eff} \approx \, 0{,}87 \cdot A[/math]
- Dementsprechend geht auch die Induktionsspannung auf 87% zurück und beträgt nur noch:
- [math]U_i=0{,}87 \cdot 165\,\rm mV = 144\,\rm mV[/math]
- Die Überlegung stimmt auch noch für eine beliebige krummlinig begrenzte Fläche. In diesem Fall kann man die Fläche durch kleine Rechtecke ausfüllen, was bis auf kleinere Lücken geht. Verwendet man nun immer kleinere Rechtecke, so werden die Lücken und somit der Fehler immer kleiner. Das Vorgehen ist nichts anderes als die Berechnung der Fläche mit einem Integral.
Eine Spule taucht ein
Eine Spule wird innerhalb von 2 Sekunden in ein homogenes Magnetfeld mit einer Feldstärke von 1000A/m senkrecht zu den Feldlinien eingetaucht. Die Spule hat einen quadratischen Querschnitt von 5cm Kantenlänge und 300 Windungen. Sie ist an ein Spannungsmessgerät angeschlossen.
a) Berechnen Sie die gemessene Induktionsspannung.
- Die Induktionsspannung berechnet sich aus der Änderung des magnetischen Flusses. Vor dem Eintauchen in das Feld ist die wirksame Fläche der Schleife noch Null und es gibt keinen Fluss durch die Schleife. Während des Eintauchens gehen wir davon aus, dass die Fläche gleichmäßig bis auf die gesamte Schleifenfläche ansteigt.
- [math]U_i = n\,\dot \Phi = n\, \frac{\Delta \Phi}{\Delta t}[/math]
- Den magnetischen Fluss berechnet man aus Feldstärke und Fläche:
- [math] \begin{array}{rcl} U_i &=& n\,\frac{\mu_0\, H\, \Delta A}{\Delta t} \\ &=& 300\cdot \frac{1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \, 1000 {\rm \frac{A}{m}} \, (0{,}05\,\rm m)^2}{2\,\rm s}\\ &=& 300\cdot \frac{3{,}14\cdot 10^{-6} \,\rm Vs}{2\,\rm s}\\ &=& 300\cdot 1{,}57\cdot 10^{-6} \,\rm V\\ &=& 4{,}71\cdot 10^{-4} \,\rm V\\ &=& 0{,}471\,\rm mV\\ \end{array} [/math]
b) Was kann man messen, wenn die Spule innerhalb des Feldes bewegt wird?
- Befindet sich die Spule vollständig im Magnetfeld, so ändert sich der magnetische Fluss durch die Schleife nicht mehr. Deshalb wird auch keine Spannung induziert.
c) Kennzeichnen Sie die Polung der Induktionsspannung mit + und - in der Zeichnung.
- Mit Hilfe der UVW-Regel / Drei-Finger-Regel erhält man die Kraftwirkung auf die Ladungen im Kabel der Schleife. Die positive Ladung wird also nach rechts gedrückt und deshalb entsteht auf dieser Seite des Spannungsmessgerätes auch ein positiver Ladungsüberschuß. (Betrachtet man die Elektronen im Kabel, verwendet man die linke Hand. Die Elektronen werden nach links gedrückt und man erhält das gleiche Ergebnis.)
Magnet im freien Fall
Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein Oszilloskop angeschlossen.
- Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung qualitativ in ein Koordinatensystem und erläutern Sie ihr Ergebnis.
|
Nach dem Induktionsgesetz wird eine Spannung induziert, wenn sich der magnetische Fluss [math]\Phi = B \cdot A[/math] durch die Spule ändert.
|
Der magnetische Fluss entspricht in der animierten Zeichnung der Anzahl der Flussdichtelinien durch die Spule. Am blauen Punkt läßt sich der Magnet verschieben. |
Energieübertragung
Transformator
- a) Warum kann man einen Transformator nicht mit Gleichstrom, sondern nur mit Wechselstrom betreiben?
- Der Transformator arbeitet mit Induktionsspannung. Eine Induktionsspannung gibt es aber nur, wenn sich innerhalb einer Spule der magnetische Fluss verändert. Bei Gleichstrom hätte man aber keine Veränderung, sondern, wie der Name schon sagt, ein zeitlich konstanten magnetischen Fluss.
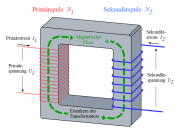
- b) Erläutern Sie anhand der Zeichnung die Funktionsweise eines Trafos.
-
- Der Trafo besteht aus zwei Spulen, die um einen gemeinsamen Eisenkern gewickelt sind. An eine davon, der sogenannten "Primärspule", legt man eine Wechselspannung an.
- Der durch die Primärspule fließende Strom verursacht ein Magnetfeld im Inneren der Spule, wodurch die Elementarmagnete des Eisen ausgerichtet werden: Der Eisenkern wird magnetisiert.
- Weil Stärke und Richtung des Stroms sich ständig ändern, ändern sich auch die Stärke und Richtung der Magnetisierung ständig. Das heißt, der magnetische Fluss durch den Eisenkern ändert sich ständig! Das wiederum ruft eine Induktionsspannung bei der zweiten Spule, der sogenannten "Sekundärspule" hervor, die auch eine Wechselspannung ist.
- Die Größe der Induktionsspannung ist abhängig von der Windungszahl der Sekundärspule. Haben Primär- und Sekundärspule die gleiche Anzahl von Windungen, so erhält man als Sekundärspannung, bis auf auftetende Verluste, die Primärspannung. Will man eine größere Spannung haben, verwendet man mehr Windungen, will man eine kleinere Spannung haben, verwendet man weniger Windungen.
- In der Zeichnung hat die Primärspule ca. 15 Windungen und die Sekundärspule ca. 6 Windungen. Die Sekundärspannung beträgt daher ungefähr die Hälfte der Pimärspannung, genauer: [math]U_2=\frac{6}{15}\, U_1 = 0{,}4 \, U_2[/math].
- c) Wie könnte der Trafo eines Netzgerätes gebaut sein, der ein Handy mit 5,7V Spannung versorgt?
- An der Steckdose liegt eine Wechselspannung mit der effektiven Spannung von 230V an. Der Trafo muß also weniger Sekundärwindungen als Primärwindungen haben, damit die Sekundärspannung kleiner ist als 230V. Das Verhältnis der Spannungen beträgt: [math] \frac{230\,\rm V}{5{,}7\,\rm V}\approx 40 [/math].
- Also muss die Primärspule 40 mal mehr Windungen haben, als die Sekundärspule, zum Beispiel 4000 Windungen, und die Sekundärspule nur 100 Windungen.
- Wer lieber mit Formeln rechnet, kann auch mit der Verhältnisgleichung arbeiten:
- [math] \begin{array}{rrcll} & \frac{U_1}{U_2} &= & \frac{n_1}{n_2} \\ & \frac{230\,\rm V}{5{,}7\,\rm V} &= & \frac{n_1}{n_2} \\ \Rightarrow & 40 &\approx& \frac{n_1}{n_2} & | \cdot n_2 \\ \Rightarrow & 40 \, n_2 &\approx& n_1 & \\ \end{array} [/math]
- d) Ein elektrisches Schweißgerät wird an europäische Netzspannung angeschlossen. Es hat eine Primärspule mit 500 Windungen und eine Sekundärspule mit nur 5 Windungen. Der ohmsche Widerstand der Sekundärspule beträgt ca. [math]0{,}011 \,\rm \Omega[/math].
- Welche Spannung liegt an der Sekundärspule an und wie groß ist dort die Stromstärke?
- Die Spannung ist proportional zur Windungsanzahl:
- [math] \begin{alignat}{2} \frac{U_1}{n_1}&= \frac{U_2}{n_2} & \quad |\,\cdot \, n_2 \\ \Rightarrow \quad U_1 \cdot \frac{n_2}{n_1} &= U_2 \\ 230\,\rm V \cdot \frac{5}{500} &= 2{,}3\,\rm V\\ \end{alignat} [/math]
- Die Stromstärke ergibt sich nach dem Ohmschen Gesetz:
- [math] \begin{alignat}{2} R&= \frac{U}{I} & \quad |\,\cdot I \quad|\, \mathopen: R \\ \Rightarrow \quad I &= \frac{U}{R} = \frac{2{,}3\,\rm V}{0{,}011\,\rm \Omega} &= 209\,\rm A \\ \end{alignat} [/math]
- Welche Leistung hat das Schweißgerät?
- Die Leistung berechnet sich aus Spannung und Stromstärke:
- [math]P = U \rm I = 2{,}3\,\rm V \cdot 109\,\rm A = 481\,\rm W [/math]
- (Weil die Leistung der Primärspule ungefähr gleich ist, beträgt die Stromstärke durch die Primärspule nur [math]2{,}1\,\rm A[/math].)
Ein schwingender Magnet
Der Nordpol eines Stabmagneten schwingt innerhalb einer Spule auf und ab. Sobald man die Spule mit einem Kabel kurzschließt, wird der Magnet gebremst und bleibt schließlich stehen.
- a) Erklären Sie diese Beobachtung.
- Am einfachsten ist es, den Weg der Energie zu verfolgen:
- Zu Beginn steckt man durch Hochheben oder Anschubsen Energie in die Schwingung. Danach wechselt die nur ihre Form (ihren Träger), bleibt aber in der Summe in etwa konstant, was man an der konstanten Amplitude der Schwingung sehen kann.
- Durch die Bewegung des Magneten wird zwar in der Spule eine Spannung induziert, aber kaum Energie übertragen.
- Erst mit dem Kurzschließen der Spule fließt die Energie aus der Schwingung heraus, die Schwingung wird abgebremst. Denn nun kann in der Spule Strom fließen, dass heißt, die Schwingung treibt mit ihrer Energie den Stromfluss an. Weil die Kupferdrähte der Spule dem Strom einen Widerstand entgegensetzen, werden die Drähte warm. Die Energie der Schwingung steckt am Ende des Vorgangs also in der Wärmeenergie des Kupferdrahtes, bzw. wird auf die im Draht erzeugte Entropie umgeladen.
- b) Was würde passieren, wenn man den Versuch mit einer supraleitenden Spule durchführen würde?
- Eine supraleitende Spule hat keinen ohmschen Widerstand, der elektrische Strom fließt ohne dass die Spule sich erwärmt. Das System aus schwingendem Magneten und Spule ist fast abgeschlossen, es verliert nur ein bischen Energie durch die Luftreibung und die innere Reibung der Feder.
- Fließt Strom durch die Spule, so baut sich ein Magnetfeld auf, in dem Energie gespeichert wird. Diese Energie wird der Schwingung entzogen, wenn der Magnet sich auf die Spule zu bewegt. Dann vergrößert sich der magnetische Fluss, eine Spannung wird induziert und der Strom angetrieben. Entfernt sich der Magnet von der Spule, so wird das Magnetfeld abgebaut und die Feldenergie fließt wieder in die Bewegung zurück. Der Magnet wird also bei der Bewegung auf die Spule zu abgebremst und bei der Bewegung von der Spule weg beschleunigt.
- Dadurch schwingt der Magnet mit einer höheren Frequenz als ohne die Spule.
- Dieser Effekt tritt bei der "normalen" Spule nicht auf, die beschleunigende Wirkung entfällt hier, denn die Spule entzieht dem System durch den ohmschen Widerstand die im Feld gespeicherte Energie.
- Will man das Geschehen quantitativ fassen, so kann man die Energie der Spule mit dem magnetischen Fluss durch die Spule berechnen:
- [math]W = \frac{1}{2}\,L\,I^2 = \frac{1}{2}\,n\Phi\,I = \frac{(n\,\Phi)^2}{2\,L} [/math]
- Zu jeder Position des Magneten gehört ein bestimmter magnetischer Fluss, aus dem man die Energiemenge der Spule berechnen kann. Die räumliche Änderung der magnetischen Energie gibt die Kraftwirkung auf den Magneten an.
Ein fallender Magnet
Ein Magnet fällt durch ein Kupferrohr
- a) Was kann man beobachten?
- Der Magnet fällt langsam, mit einer konstanten Geschwindigkeit durch das Rohr.
- b) Wieso kann man für den Versuch kein Plastikrohr und auch kein Eisenrohr verwenden?
- In einem Plastikrohr können keine Ströme induziert werden, der Effekt bleibt aus. Das wird hier ausführlich erläutert.
- Das Eisenrohr dagegen kann magnetisiert werden und der Magnet fällt gar nicht, sondern bleibt am Rohr hängen.
- c) Wie verändert sich das Versuchsergebnis, wenn man ein Kupferrohr mit dickeren Wänden benutzt?
- Bei einer bestimmten Geschwindigkeit wird immer die gleiche Spannung induziert, unabhängig von der Dicke des Rohres. Aber je dicker die Wand, desto geringer ist der elektrische Widerstand. Deshalb fließt bei der gleichen Geschwindigkeit mehr Energie pro Zeit aus der Bewegung, der Magnet wird stärker gebremst:
- [math]P = U\, I = \frac{U^2}{R}[/math]
- [math]P = F_{mag}\,v[/math]
- Das Gleichgewicht aus Gewichtskraft und magnetischer Kraft stellt sich daher bei einer geringeren Geschwindigkeit ein.
- d) Wie könnte man es erreichen, dass der Magnet schwebt?
- Dazu muß der elektrische Widerstand vollständig verschwinden, was man bei einem Supraleiter tatsächlich auch erreichen kann! (Siehe diese Demonstration der Harvard-University)
Induktionskochplatte
- Erklären Sie in Text und Bild, wie eine Induktionskochplatte funktioniert.
- Was man bei einem Transformator vermeiden möchte ist hier das Wirkungsprinzip.
- Zur Erklärung nehmen wir vereinfachend an, dass sich nur eine große Spule unter dem Topf befindet. Die Spule ist an eine hochfrequente Wechselspannung angeschlossen, wodurch der Topfboden von einem sich ständig ändernden Magnetfeld durchsetzt wird. Deshalb fließt im Boden um das Magnetfeld ein Kreisstrom, der, wegen des ohmschen Widerstandes des Bodens, den Boden erhitzt.
- Ein zweiter Erwärmungseffekt stellt sich dadurch ein, dass der Topfboden ständig ummagnetisiert wird. Dies geschieht nicht verlustfrei, sondern führt auch zu einer Erwärmung des Bodens.
- Induktionsherde haben in der Regel eine hitzebeständige Glasplatte als Topfauflage. Warum erhitzt der Herd nur den Topf und nicht das darin befindliche Essen oder die Glasplatte? (Warum wird die Glasplatte beim Kochen trotzdem heiß?)
- Sowohl Glas als auch das Essen können den elektrischen Strom nicht leiten und sind nicht magnetisierbar. Sie werden aber, hauptsächlich durch Wärmeleitung, indirekt vom heißen Topfboden erwärmt.
Wirbelstrombremse
- Nennen Sie Beispiele, bei denen eine Wirbelstrombremse eingesetzt wird.
- In diesem Wikipediaartikel sind sehr schöne Beispiele genannt und erläutert. (Züge, Achterbahnen und Falltürme, Fitnessgeräte, LKWs, Messgeräte)
- Erläutern Sie das Funktionsprinzip mit einer Zeichnung.
- Erklären Sie dabei mit Hilfe des Induktionsgesetzes, wie die Ströme fließen.
- Linke Seite der Zeichnung: Tritt der Leiter in das Magnetfeld ein, so vergrößert sich senkrecht dazu die magnetische Feldstärke und damit der magnetische Fluß. Um diese Stelle herum entsteht deswegen eine Induktionsspannung, die einen Strom im Leiter antreibt. Durch diesen Strom im Leiter wird ein Magnetfeld erzeugt, dass dem Feld des Permanentmagneten entgegengesetzt ist (rechte Hand-Regel). Dadurch werden Leiter und Permanentmagnet voneinander weggedrückt, der Leiter gebremst.
- Rechte Seite der Zeichnung: Tritt der Leiter aus dem Magnetfeld aus, so verringert sich der magnetische Fluß und die Induktionsspannung ist umgekehrt gerichtet. Durch den Strom im Leiter wird wiederum ein Magnetfeld erzeugt, dass diesmal parallel zum Feld des Permanentmagneten ist (rechte Hand-Regel). Dadurch werden Leiter und Permanentmagnet zueinander gezogen, auch hier wird der Leiter gebremst.
- Insgesamt wird also vom Magneten am Leiter auf der linken Seite nach links gedrückt und auf der rechten Seite nach links gezogen. Der Leiter wird abgebremst.
- Wie kann man die Bremswirkung mit der Energieerhaltung begründen?
- Zunächst wird etwas Energie benötigt, um den Stromfluss in Gang zu setzen und damit ein Magnetfeld aufzubauen. Die meiste Energie wird aber zur Erhaltung des Stromflusses benötigt. Durch den ohmschen Widerstand des Leiters wird nämlich der Leiter erwärmt und die dazu nötige Energie dem Magnetfeld der Ströme entzogen. Sämtliche benötigte Energie wird der Bewegung des Leiters entzogen, der Leiter wird also abgebremst.
Spule und Magnetfeld als Energiespeicher
Selbstinduktion
- a) Erklären Sie den Begriff der Selbstinduktion indem Sie einen passenden Versuch beschreiben.
- Auf dieser Seite wird das An- und Ausschalten eines Stromkreises mit Spule beschrieben.
- b) Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist.
- Nach dem Induktionsgesetz ist die Induktionsspannung proportional zur Änderung des magnetischen Flusses.
- Der magnetische Fluss berechnet sich aus dem Produkt von Fläche [math]A[/math] und Flussdichte [math]B[/math] , bzw. Feldstärke [math]H[/math].
- Die magnetische Feldstärke einer (langen) Spule berechnet sich dann mit Hilfe der Stromstärke, der Windungsanzahl und der Länge der Spule. (Herleitung).
[math] \begin{align} U_i &= - n \, \dot \Phi \\ &= - n \, \dot{( A\, B )} = - n \, A\, \dot B \\ &= - n \, A\, \mu_0 \, \dot H \\ &= - n \, A\, \mu_0 \, n \, \frac{\dot I}{l} \\ \end{align} [/math]
- Im Endeffekt ist die Änderung des magnetischen Flusses also nur von der Änderung der Stromstärke abhängig, bzw. dazu proportional.
Induktivität und Energiegehalt einer Spule
- a) Eine Spule hat eine Induktivität von 10 H (Henry).
- Was bedeutet das? Erläutern Sie es anhand von Verwendungsbeispielen.
- Ändert sich die Stromstärke in der Spule pro Sekunde um 1A, so wird in der Spule eine Spannung von 10V induziert.
- b) Eine Spule hat 1000 Windungen, eine Querschnittsfläche von 3cm x 3cm und eine Länge von 10cm.
- a) Berechnen Sie ihre Induktivität.
- [math]A= 0{,}03\,\rm m \cdot 0{,}03\,\rm m = 9 \cdot 10^{-4}\,\rm m^2[/math]
- [math]L= \mu_0 \, \mu_r \, \frac{A\, n^2}{l} = 1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 1 \cdot \, \frac{ 9 \cdot 10^{-4}\,\rm m^2 \cdot 1000^2}{0{,}1\,\rm m} = 11{,}3 \,\rm mH[/math]
Man läßt einen Strom mit der Stärke von 2A durch die Spule fließen.
- b) Berechnen Sie den magnetischen Fluss, die Feldstärke, die Energiemenge und die Energiedichte der Spule.
- Der magnetische Fluss berechnet sich aus Fläche und Flussdichte, bzw. Feldstärke:
- [math] \begin{align} \Phi &= A \, B = A\, \mu_0 \, H \\ &= A\, \mu_0 \, n \, \frac{I}{l} \\ &= 9 \cdot 10^{-4}\,\rm m^2 \cdot 1{,}257 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 1000\cdot \frac{2\,\rm A}{0{,}1\,\rm m} = 22{,}6 \cdot 10^{-6} \,\rm Wb = 22{,}6 \,\rm \mu Wb\\ \end{align} [/math]
- Alternativ kann man den Fluss auch mit der Induktivität [math]L[/math] berechnen:
- [math] \begin{align} \Phi &= \frac{L\,I}{n} \\ &= \frac{11{,}3 \,\rm mH \cdot 2\,\rm A}{1000} = 22{,}6 \cdot 10^{-6} \,\rm Wb\\ \end{align} [/math]
- Die Energiemenge berechnet sich zu:
- [math] \begin{align} W &= \tfrac{1}{2} L\, I^2\\ &= \tfrac{1}{2} 22{,}6 \cdot 10^{-6} \,\rm Wb\, (2\,\rm A)^2 = 45\cdot 10^{-6} \,\rm J\\ \end{align} [/math]
- Die Energiedichte ergibt sich als Energie pro Volumen:
- [math] \begin{align} \rho_W &= \frac{W}{V}\\ &= \frac{45\cdot 10^{-6} \,\rm J}{9 \cdot 10^{-4}\,\rm m^2 \cdot 0{,}1\,\rm m} = 0{,}5 \,\rm \tfrac{J}{m^2} \end{align} [/math]
Die stromdurchflossene Spule wird nun in einen geschlossenen Eisenkern mit der relativen Permeabilität von 2000 gestellt.
- c) Wie verändern sich dadurch die Werte von Frage b)?
Energie des Erdmagnetfeldes
Das Erdmagnetfeld hat in Europa eine Feldstärke von ca. 40A/m, bzw. eine Flußdichte von ca.50 MikroTesla.
- Wieviel Energie ist innerhalb Ihres Zimmers im Erdmagnetfeld gespeichert?
- Wie hoch könnte man damit eine Tafel Schokolade heben?
Feldenergie von Festmagneten
Zwei Festmagnete "haften" aneinander und werden bis auf einen Abstand von 0,5cm auseinandergezogen. Wieviel Energie war wohl dazu nötig?
Näherungsweise nimmt man das Feld zwischen den Polen als homogen an. Die Feldstärke zwischen den Polen wird zu 120000A/m gemessen. (Die Flußdichte beträgt 0,15T.)
supraleitender Energiespeicher
Supraleiter sind Materialien, die bei niedrigen Temperaturen keinen ohmschen Widerstand mehr haben. Daraus kann man supraleitende Kabel herstellen und auch Spulen wickeln.
- a) Entwerfen Sie eine supraleitende Spule, welche die Energie eines Liters Benzin (ca. 40MJ) speichern kann.
- b) Welche Vor- und Nachteile hätte die Verwendung eines Eisenkerns?
Bewegungsenergie der Elektronen
Bei einer stromdurchflossenen Spule bewegen sich die Ladungsträger, in diesem Fall also die Elektronen. In dieser Bewegung steckt auch Energie. Vielleicht ist dort auch die Energie der Spule gespeichert und nicht im Magnetfeld? Als Beispiel nehmen wir eine Spule mit 1000 Windungen, einer Querschnittsfläche von 3cm x 3cm und einer Länge von 10cm.
Zunächst muss man die Masse der im Kupferdraht frei beweglichen Elektronen berechnen. Der Draht hat eine Masse von 120g. Jedes Kupferatom stellt ungefähr ein Leitungselektron zur Verfügung. Die Dichte von Kupfer beträgt ca. 9 g/cm^3 und das molare Volumen beträgt ca. 7*10^-6 m^3/mol.
- a) Wieviel Masse haben die Leitungselektronen des Kupferdrahtes?
- b) Welche Geschwindigkeit müßten die Elektronen haben, um die Energie bei einer Stromstärke von 2A zu speichern?
Elektrische Wirbelfelder
Fußnoten
- ↑ Das entspricht einer magnetischen Flussdichte von [math]B = \mu_0\, H_h = 1{,}26 \cdot 10^{-6} \frac{\mathrm{V\,s}}{\mathrm{A\,m}} \cdot 16\,\rm \frac{A}{m} = 20{,}16 \cdot 10^{-6} \frac{V\, s}{m^2} \approx 20 \cdot 10^{-6} \frac{Wb}{m^2} = 20\,\rm \mu T [/math]
- ↑ Diese Formel zur Berechnung der Spannung an einer Spule in Abhängigkeit von der Stromstärkeänderung spielt bei der Induktivität einer Spule eine Rolle.